Двойственные задачи линейного программирования

1.Общая задача линейного программирования

Двойственная задача - это вспомогательная задача ЛП, формулируемая с помощью определенных правил непосредственно из условий исходной, или прямой, задачи. Приведем обобщенную формулировку двойственной задачи ЛП, которая применима к любой форме представления прямой задачи(приводимая ниже формулировка двойственной задачи является обобщенной в том смысле, что она применима ко всем формам прямой задачи).

Для математической задачи: всегда можно построить двойственную задачу вида:

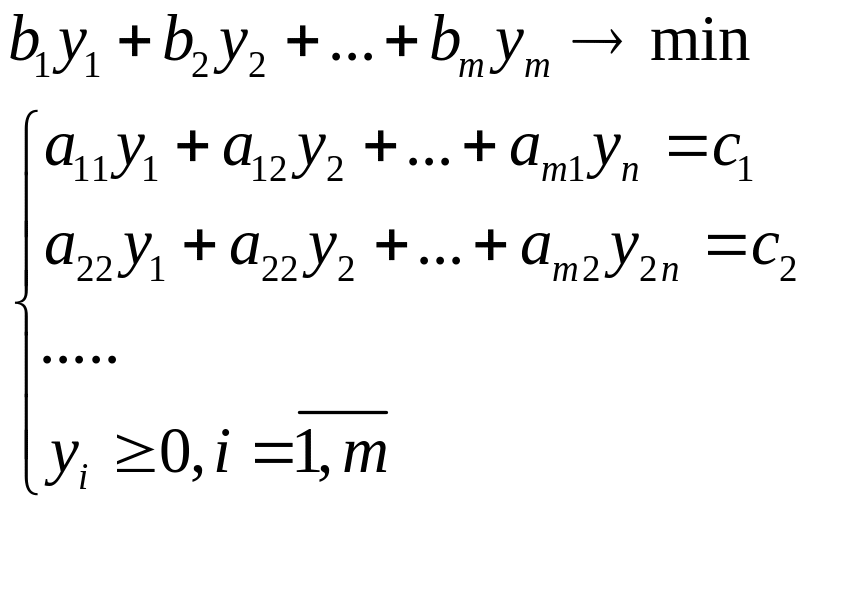
Правила составления двойственной задачи по отношению к исходной:

1)число переменных двойственной задачи=числу ограничений прямой задачи;

2)коэф-тами к целевой функции дв.задачи яявляются правые части ограничений прямой задачи;

3)если исходная задача на max то двойственная на min;

4)матрица коэф-тов системы ограничений дв.задачи получается путем транспонирования матрицы коэф-тов системы ограничений прямой задачи;

5)если ограничения исх.задачи имеют ограничения <=, ограничение дв.задачи >= и наоборот;

6)правыми частями ограничений дв.задачи явл-ся коэф-ты цел.функции прямой задачи;

7)условия неотрицательности в обоих задачах сохраняются.

2. Экономическая интерпретация двойственной задачи

Пусть имеется задача о наилучшем использовании рес-ов:

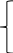C₁X₁+… +C_NX_N→ max x – количество продукции

a₁x₁+… +a_1nx_n<=b₁ c – цены на сбыт

(1) … … … aij – кол-во ресурсов iго типа на производства продукта j

a_m1x₁+…+a_mnx_n<=b_m bi – ограничение по I ресурсу на складе

x_j>=0, j=1,n

Пусть У_i – цена 1 единицы i вида ресурса. Тогда за все рес-сы фирма заплатит: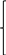

b₁y₁+…+ b_my_m→ min

a₁₁y₁+ a₂₁y₂+…+ a_m1y_m>=c₁

(2) … … …

a_1ny₁+ …+ a_mny_m>=c_n

y_i>=0, i=1,m

О бщий вид задачи:

C₁X₁+… +C_NX_N→ max b₁y₁+…+ b_my_m→ min

a₁x₁+… +a_1nx_n<=b₁

(1) … … … a_ny₁ + a₂₁y₂+…+a_m1y_m>=c₁ :x₁

a_m1x₁+…+a_mnx_n<=b_m1

a_m1+1x₁+…+a_m+1nx_n<=b_m1+1 (2) a_1n1y₁ + …+a_mn1y_m>=c_n1 :x_n1

… … …

a_m1x₁+…+a_mnx_n=b_m a_1n1+1y₁ + …+a_mn1+1y_m=c_n1+1 :x_n1+1

x_j>=0, j=1,n;n₁<=n a_1ny₁+ …+ a_mny_m>=c_n :x_n ; y_i>=0, i=1,m

Ограничения на знак в дв.задаче будут иметь только те переменные, которые имеют ограничения типа нер-ва.

Двойственная оценка показывает насколько увеличится значение целевой функции, если значение соотв-го рес-са увеличить на 1 единицу.

3 . Основное неравенство двойственности

C₁X₁+… +C_NX_N→ max b₁y₁+…+ b_my_m→ min

a₁x₁+… +a_1nx_n<=b₁ :У₁ a_ny₁ + a₂₁y₂+…+a_m1y_m>=c₁

(1) a_m1x₁+…+a_mnx_n<=b_1т :у_ь (2) a_1m1y₁ + …+a_mn1y_m>=c_n

x_j>=0, j=1,n; y_i>=0, i=1,m

Для любых допустимых планов прямой и двойственной задачи ЛП справедливо неравенство:

Доказательство: из дв.задачи (2)

Для любого допустимого плана пр-ва Х и любого доп-го вектора оценок У (с₁х₁+…+ с_nх_n) общая стоимость произведенной продукции не превосходит суммарной оценки рес-сов (b₁y₁+…+ b_my_m) .

4. Теоремы двойственности

1. Критерий оптимальности Канторовича.Если для некоторых допустимых планов х* и у* пары двойственных задач (1)и(2) выполняется равенство f(x)=g(y): C₁X₁+… +C_NX_N= b₁y₁+…+ b_my_m, то х* и у* являются оптимальными планами соответствующих задач.Док-во. Согласно основному неравенству двойственности, для любого допустимого плана х* прямой задачи и допустимого плана у двойственной справедливо неравенство g(y) < f(x*). Но по условию g(y*) = f(x*). Отсюда в силу транзитности отношений < и =, получим g(y)< g(y*). Так как у – произвольный план, то g(y*) есть максимальное значение целевой функции, то есть у – оптимальный план двойственной задачи. Аналогично доказывается, что х* является оптимальным для прямой задачи.

2.Основная теорема дв-ти:Если одна из задач двойственной пары имеет оптимальное решение, то и другая имеет оптимальное решение. Если же 1 из дв-ных задач не имеет решений на мн-ве доп.планов вследствии неограниченности целевой функции, то и 2 не имеет решения в силу пустоты мн-ва доп.планов. Т.е. если прямая задача имеет опт.решение, то дв-ная к ней также имеет опт.решение. Причем значение цел.функции на опт.планах прямой и дв-ной задач совпадают: F(X^*)=G(Y^*)

Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов.

3.Теорема о дополняющей нежесткости:

Для того чтобы X^*=( X₁^*, .. X_n^*) и У^*=( У₁^*, .. У_n^*) являлись оптим. планами прямой и двойственной задач, необх-мо и дост-но, чтобы выполнялись след.соотношения:

               Экономически это означает, что если по некоторому оптимальному планупроизводства расход i -го ресурса строго меньше его запаса, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его i -я компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку.