РЫБИНСКАЯ ГОСУДАРСТВЕННАЯ АВИАЦИОННАЯ ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ

Имени П.А. Соловьёва

Кафедра «АВИАЦИОННЫЕ ДВИГАТЕЛИ»

Лаборатория «ТЕРМОДИНАМИКА И ТЕПЛОПЕРЕДАЧА»

ЛАБОРАТОРНАЯ РАБОТА

«ОПРЕДЕЛЕНИЕ ТЕПЛОЕМКОСТИ ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ»

РЫБИНСК, 2009 г.

Содержание

ВВЕДЕНИЕ 3

Газ 13

2.1 Установка 16

2.2 Блок сопряжения 17

2.3 Программная часть 18

2.3.1 Файлы программы 18

2.3.2 Работа с программой 18

ВВЕДЕНИЕ

Цель работы – определение методом калориметрирования теплоемкости воздуха при постоянном давлении.

Прежде чем приступить к работе, необходимо усвоить элементарные вопросы теории теплоемкости.

В процессе выполнения работы требуется определить из эксперимента изобарную теплоемкость воздуха и составить по проделанной работе отчет.

1. Теоретические основы

1.1 Понятие о теплоемкости

Теплоемкостью тела (системы тел) называется отношение количества теплоты, поглощенной телом в определенном термодинамическом процессе, к изменению его температуры

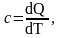(1)

где dQ – элементарное количество теплоты;

dT – элементарное изменение температуры.

В зависимости от количественной единицы тела, к которому подводится теплота, различают:

- массовую теплоемкость – с, [Дж/кг К];

- мольную теплоемкость – 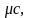[Дж/ моль К];

- объемную теплоемкость – С, [Дж/м³ К].

Соотношение между этими теплоемкостями можно получить следующим образом. Один моль газа имеет массу 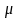кг, следовательно, массовая теплоемкость определяется из мольной теплоёмкости делением ее на молекулярную массу

. (2)

Один моль любого газа при нормальных условиях имеет объем 22,4 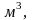поэтому объемная теплоемкость равна

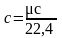(3)

Используя (3) и связь плотности, молекулярной массы и объем 1 моля газа при нормальных условиях получим

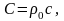(4)

отсюда

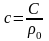, (5)

где

.

Так как теплота, подводимая в процессе к телу (системе), зависит от вида процесса, то теплоемкость будет свойством системы только тогда, когда процесс будет фиксированным, т.е. будет происходить при постоянном значении каких – либо параметров системы

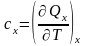, (6)

(индекс «x» при частной производной означает, что процесс идет при одном постоянном значении величины ).

Следует отметить, что рассматриваемые процессы теплообмена являются квазистатическими, потому теплоемкость будет величиной, относящейся к телу в состоянии термодинамического равновесия, и теплоемкости являются функциями параметров тела (системы), т.е.

Уравнение (6) определяет так называемые истинные теплоемкости, которые в термомеханической системе будут функциями термических параметров.

Так, теплоемкость в процессе при постоянном объеме 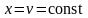согласно уравнению (6) равна

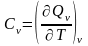, (7)

а теплоемкость в процессе, идущем при постоянном давлении x=p=const, равна

. (8)

Разность между теплоемкостями и идеального газа устанавливается формулой Майера, известной из физики и имеющей вид

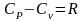. (9)

Эта формула является следствием первого закона термодинамики.

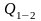Кроме истинных теплоемкостей в расчетах употребляют средние теплоёмкости , равные отношению количества теплоты, выделившейся или поглощенной в процессе , к изменению температуры 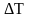при условии, что разность температур – величина конечная

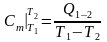. (10)

Естественно, что истинная теплоемкость

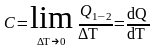. (11)