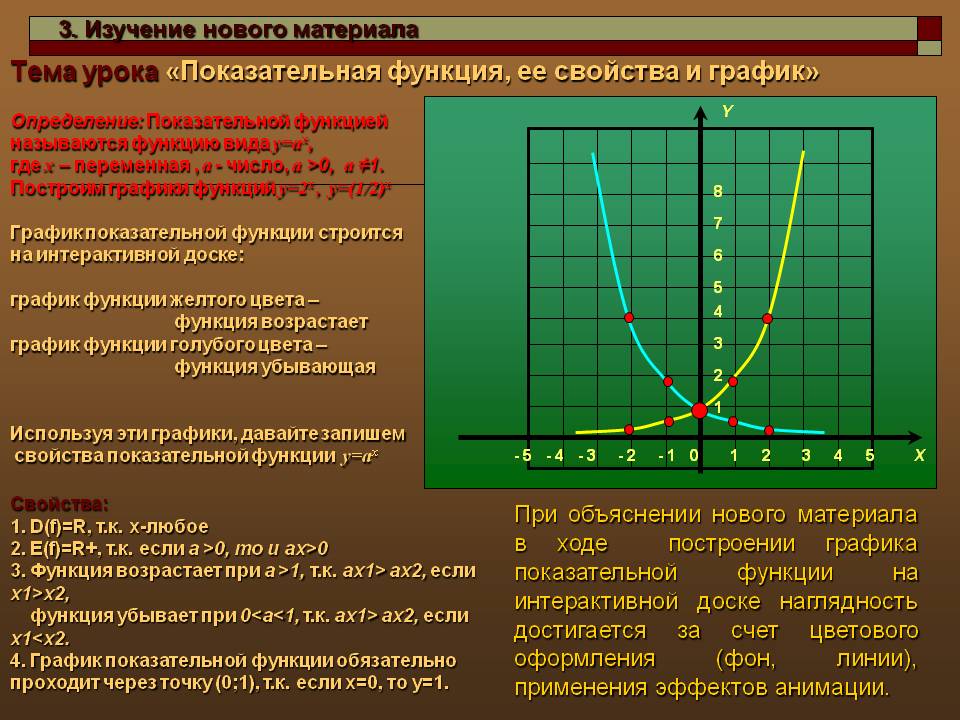
Свойства показательной функции

Область определения показательной функции - множество всех действительных чисел. Ведь положительное число а можно возвести в степень с любым показателемх.

Это значит, что график показательной функции простирается вдоль всей оси абсцисс.

Область значений показательной функции - множество всех положительных чисел. Ведь при возведении положительного числа а в степень с показателем х не может получиться ни нуля, ни отрицательного числа. Это значит, что график показательной функции не может иметь общих точек с осью абсцисс и не может иметь точек в третьей и четвертой четверти. График показательной функции простирается над всей осью абсцисс.

Из сказанного следует, что показательная функция сохраняет один и тот же знак на всей области определения - всегда положительна.

Монотонность показательной функции определяется значением основания а:

если а>1, то функция возрастает,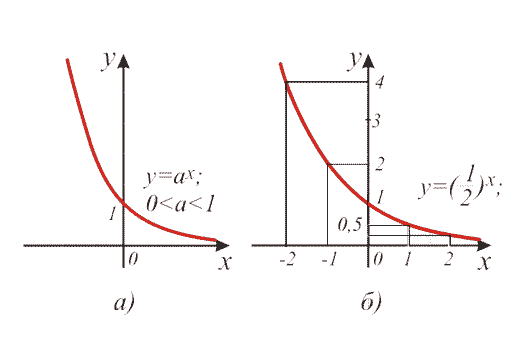 

а если а<1, то функция убывает.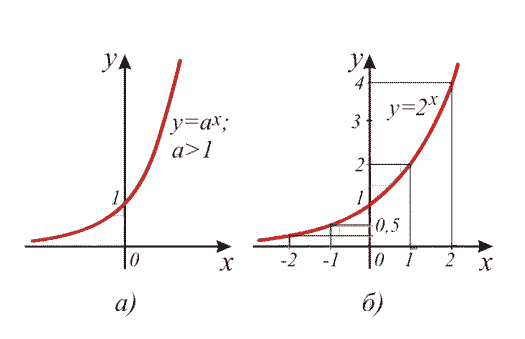 

Различно и поведение показательных функций на границах области определения.

Если а>1, то функция на отрицательной бесконечности стремится к нулю, а на положительной бесконечности стремится к бесконечности.

Если же а<1, то функция на отрицательной бесконечности стремится к бесконечности, а на положительной бесконечности стремится к нулю.

Логарифмическая функция

• Функция вида   y = log_a х (где а > 0, а ≠ 1)   называется логарифмической.

Область определения логарифмической функции — множество всех положительных чисел. Это следует из определения логарифма, так как выражение log_ax имеет смысл только при x > 0.

2) Множество значений логарифмической функции — множество R всех действительных чисел. Это следует из того, что для любого действительного числа b есть такое положительное число x, что log_ax = b, т.е. уравнение log_ax = b имеет корень. Такой корень существует и равен x = a^b, так как log_aa^b = b.

3) Логарифмическая функция y = log_ax является возрастающей на промежутке x > 0, если a > 0, и убывающей, если 0 < a < 1.

4) Если a > 0, то функция y = log_ax принимает положительные значения при x > 1,отрицательные — при 0 < x < 1. Если 0 < a < 1, то функция y = log_ax принимает положительные значения при 0 < x < 1, отрицательные — при x > 1. Это следует из того, что функция y = log_ax принимает значение , равное нулю, при x = 1 и является возрастающей на промежутке x > 0, если a > 1, и убывающей, если 0 > a > 1.

Ниже представлены графики логарифмических функций при a > 0 (1);   0 > a >1 (2).

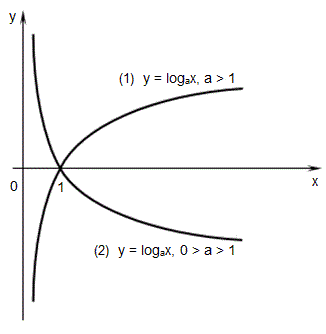
Стоит отметить, что график любой логарифмической функции y = log_ax проходит через точку (1 ; 0).

Вида y=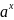 , где х – переменная, а- число, а >0 и х не равно 1.

Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени.

Решение показательных уравнений часто сводится к решению уравнения ах = аb, где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b.

34. Логарифм числа N по основанию a — это такой показатель степени x, в которую нужно возвести число a, чтобы получить число N.

1.

ax= N

2.	loga(N)= x

Для логарифма числа справедливо следующее тождество

3.	a loga(N) = N

Число a (основание логарифма), и N (число) можно брать и целыми и дробными, но обязательно положительными, если логарифм должен быть действительным, иначе он будет комплексным числом.

Само значение логарифма числа может быть и отрицательным. Отрицательные логарифмы также важны как и положительные.

Если основание логарифма a больше 1 то большее число N имеет больший логарифм

4.

a > 1

5.	N1 < N2 < … < Nm

6.	loga(N1) <loga(N2) < … <loga(Nm)

для примера

7.

a= 2

8.	log2(1) <log2(2) < … <log2(10)

Если число N > 1 (больше единицы), то логарифм числа положительный

9.

N > 1

10.	loga(N) > 0

Если число N < 1 (меньше единицы), то логарифм числа отрицательный

11.

N < 1

12.	loga(N) < 0

логарифм единицы при любом основании равен нулю

13.

N= 1

14.	loga(N)= 0

логарифм числа N равного основанию a всегда равен единице!

15.

N= a

16.	loga(N)= 1