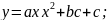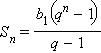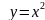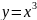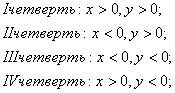http://arprog.ru/

1. Функции и их свойства. Область определения и область значения функций.

Функция – заданное правило на множество чисел. ɏ -любое число.

(Х) - аргумент функции или независимая переменная.

У - зависимая функция.

D (f) - область определения функции

E (f) – область значения функции

Свойства:

Монотонность (убывающая, возрастающая)

Ограниченность функции

Мак, Минимум

Выпуклость

Непрерывность

Четная или не четная

2. , a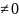

D=

D>0= два корня

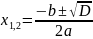
D=0, D>0.

3. 

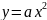всегда через начало координат

4. 

• Дискриминант, потом график

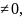
• Дискриминант, ,a 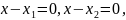метод интервалов

5. Линейное уравнение

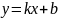,k

,

,

,

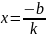6. Рациональным уравнением с двумя переменными х и y называют уравнение вида P(x;y)=0.

P=различное алгебраическое выражение.

Решением уравнения P(x;y)=0 называют всякую пару чисел, при которых выражение P(x;y)-превращается в ноль.

Пара рациональных уравнений с двумя переменными соединенные скобками называются – системой. Решением системы является пара чисел которые удовлетворяют переменную и другую переменную.

• Метод сложения:

Нужно записать два уравнения строго друг под другом: 2 –5у=61 -9х+5у=-40. Далее, сложить каждое слагаемое уравнений соответственно, учитывая их знаки: 2х+(-9х)=-7х, -5у+5у=0, 61+(-40)=21. Как правило, одна из сумм, содержащая неизвестную величину, будет равна нулю.

Составить уравнение из полученных членов: -7х+0=21.

Найти неизвестное: -7х=21, ч=21:(-7)=-3.

Подставить уже найденное значение в любое из исходных уравнений и получить второе неизвестное, решив линейное уравнение: 2х–5у=61, 2(-3)–5у=61, -6-5у=61, -5у=61+6, -5у=67, у=-13,4.

Ответ системы уравнений: х=-3, у=-13,4.

• Метод подстановки:

1. Из одного уравнения выражаем одно из неизвестных, например  x, через коэффициенты и другое неизвестное  y:

x = ( c – by ) / a .                             

2)  Подставляем во второе уравнение вместо x :

   d ( c – by ) / a + ey = f .

3)  Решая последнее уравнение, находим  y :

     y = ( af – cd ) / ( ae – bd ).

4)  Подставляем это значение вместо y  в выражение (2):

   x = ( ce – bf ) / ( ae – bd ) .

7. Арифметическая прогрессия.

Числовую последовательность {an}, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называют арифметической прогрессией.

Функция натурального аргумента называется – числовой последовательностью.

Y=f(x); x любое натуральное число.

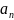- любое число

-номер числовой последовательности

Виды представления:

Словестный, Аналитический, Рекуретный.

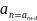
-разность арифметической прогрессии.

Если d > 0, то прогрессия является возрастающей. Если d < 0, то прогрессия является убывающей. Арифметическая прогрессия считается конечной, если рассматриваются только ее первые несколько членов. 

Формулы арифметической прогрессии:

an = a1 + d(n - 1) - формула n-го члена арифметической прогрессии;

an = ak + d(n - k) - формула нахождения n-го члена арифметической прогрессии через k -ый член прогрессии;

Сумма n членов арифметической прогрессии:

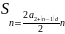
8. Если |q| > 1, то прогрессия называется возрастающей. Если |q| < 1, то прогрессия называется убывающей.

Геометрическая прогрессия считается конечной, если рассматриваются только ее первые несколько членов.

Числовую последовательность {bn}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q ≠ 0, называют геометрической прогрессией: q - знаменатель прогрессии

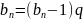
Каждый член геометрической прогрессии {b_n} определяется формулой 

bn = b1 · qn – 1.

Сумма n первых членов геометрической прогрессии {bn} равна

Формула суммы бесконечной геометрической прогрессии

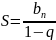; q 1

.

Степенная функция. Это функция:  y = axn, где a, n – постоянные. При n = 1 получаем прямую пропорциональность: y = ax; при n = 2 -квадратную параболу ; при n = 1 - обратную пропорциональность или гиперболу. Таким образом, эти функции - частные случаи степеннойфункции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, cледовательно, приn = 0 степенная функция превращается в постоянную величину:  y = a, т.e. её график - прямая линия, параллельная оси  Х, исключая начало координат ( поясните, пожалуйста, почему ? ).Все эти случаи ( при  a = 1 ) показаны на рис.13  ( n   0 ) и рис.14 ( n < 0 ). Отрицательные значения  x здесь не рассматриваются, так как тогда некоторые функции:

Степенной функцией с вещественным показателем a называется функция y = x ⁿ , x > 0.

Заметим, что для натуральных n степенная функция определена на всей числовой оси.  Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x .

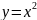• ; n=2

D(y)=R

E(y)=(0, )

(

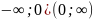
Четная

F(x); f(x)=f(x)

• 

• 

• 

D(f)=R

E(f)=R

Возрастает (

Неограниченна

Функция выпукла вверх (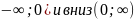

Нечетная

• ;

• 

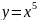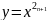
D(f)=R, кроме x=0

E(f)=R, кроме y=0

Функция убывает по всей своей функции

Неограниченна

Монотонна

Выпукла вверх и вниз

Нечетная

• или

D(f)=R, кроме x=0

E(f)=R, кроме y=0

Ограниченна

Монотонна

Выпуклая вниз

Четная

Пусть a 0 и n N n =1.  Тогда существует единственное неотрицательное число x такое, что выполняется равенство xn=a.  Это число называется арифметическим корнем n-ной степени из неотрицательного числа и обозначается  na .  При этом число a называется подкоренным числом , а число n - показателем корня.  Вместо слова «корень» часто говорят радикал .  Если n = 2, то обычно пишут просто:  a .  При n = 2 арифметический корень называется квадратным корнем,  при n = 3 говорят о кубическом корне .

Итак, по определению:  x= na a 0    xn=a  x 0    . Отсюда следует, что ( na)n=a .

Действия с корнями

• Величина корня не изменится, если его показатель увеличить в n раз и одновременно возвести подкоренное значение в степень n.

• Величина корня не изменится, если показатель степени уменьшить в n раз и одновременно извлечь корень n-й степени из подкоренного значения.

• Корень из произведения нескольких сомножителей равен произведению корней той же степени из этих сомножителей.

• Обратно, произведение корней одной и той же степени равно корню той же степени из произведения подкоренных значений.

• Корень от частного равен частному от деления корня из делимого на корень из делителя (показатели корней должны быть одинаковыми).

• Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение.

• Обратно, чтобы извлечь корень из степени, достаточно возвести в эту степень корень из основания степени.

Свойства. При k n N n =1 k =1  справедливы следующие свойства корней.

• =

• =

• =

• 

• 

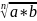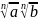
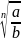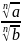
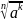
Если a < 0, а n=2k k N , то не существует такого действительного x , при котором бы выполнялось равенство xn=a. Следовательно, невозможно ввести понятие корня четной степени из отрицательного числа. Однако определить понятие корня нечётной степени из отрицательного числа всё же возможно. В самом деле, пусть a < 0, а n - нечётное число, тогда существует единственное число x такое, что xn=a. Это число и называется корнем нечетной степени из отрицательного числа . Оно обозначается точно так же:  na . Например,  3−8=−2  так как (-2)³= -8. Для нечетных показателей степени свойства, справедливые для неотрицательных значений подкоренных выражений, верны также и для отрицательных значений подкоренных выражений.

11. Вместо слова «корень» часто говорят радикал . 

Свойства. При k n N n 1 k 1  справедливы следующие свойства корней.

• =

• =

• =

Радикал - Математический знак действия извлечения корня.

12. В 7-м и 8-м классах вы выполняли преобразования рациональных выражений, используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т.д. В 8-м классе вы изучили новую операцию — операцию извлечения квадратного корня из неотрицательного числа и, используя свойства квадратных корней, выполняли преобразования выражений, содержащих квадратные корни. В предыдущих параграфах мы познакомились с операцией извлечения корня п-й степени из действительного числа, изучили свойства этой операции, а именно (для неотрицательных значений а и b).

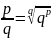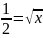Если правильная дробь обыкновенная, и а >0, то а x , x .

Если правильная дробь и а > 0, то а = .

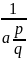14. Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе (или, что эквивалентно, зависимость хорд и высот отцентрального угла в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.

К тригонометрическим функциям относятся:

прямые тригонометрические функции

• синус (sin x)- это отношение катета лежащего против гипотенузы

• косинус (cos x)- к прилежащему гипотенузе.

производные тригонометрические функции

• Синусом называется отношение 

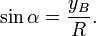
• Косинусом называется отношение 

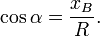
• Тангенс определяется как 

• Котангенс определяется как 

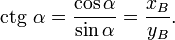
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:

• Синусом угла α называется отношение AB/OB (отношение противолежащего катета к гипотенузе).

• Косинусом угла α называется отношение ОА/OB (отношение прилежащего катета к гипотенузе).

• Тангенсом угла α называется отношение AB/OA (отношение противолежащего катета к прилежащему).

• Котангенсом угла α называется отношение ОА/AB (отношение прилежащего катета к противолежащему).

15. Определение. Дана единичная окружность, на ней отмечена начальная точка A — правый конец горизонтального диаметра. Поставим в соответствие каждому действительному числу t точку окружности по следующему правилу:

1) Если t > 0, то, двигаясь из точки A в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь AM длины t. Точка M и будет искомой точкой M(t).

2) Если t < 0, то, двигаясь из точки A по часовой стрелке (отрицательное направление обхода окружности), опишем по окружности путь AM длины |t|. Точка M и будет искомой точкой M(t).

3) Числу t = 0 поставим в соответствие точку A; A = A(0). Единичную окружность с установленным соответсвием (между действительными числами и точками окружности) будем называть числовой окружностью.

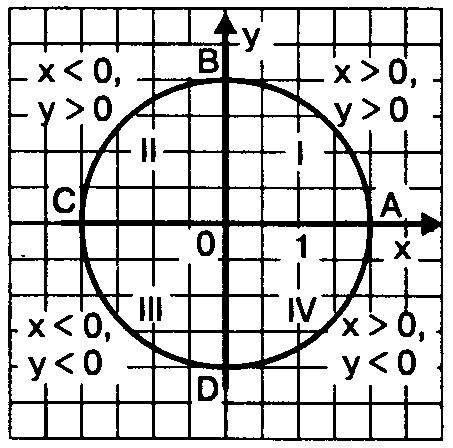
16. Числовая окружность на координатной плоскости

Расположим числовую окружность в декартовой прямоугольной системе координат x0y так, как показано на рисунке:

Каждая точка числовой окружности имеет в системе x0y свои координаты, причем для точек:

Для любой точки M(x; y) числовой окружности выполняются неравенства:

-1≤ x ≤1; -1≤ y ≤1;

Уравнение данной чсиловой окружности имеет вид:

Синус и косинус Определение. Если точка M числовой единичной окружности соответсвтует числу t, то абсциссу точки Mназывают косинусом числа t и обозначают cost, а ординату точки M называют синусом числа t и обозначают sint. Итак, Отсюда следует, что Так как каждая точка имеет свои координаты, можно составить таблицу значений синуса и косинуса по четвертям окружности Четверть окружности 1-я 2-я 3-я 4-я cost + - - + sint + + - - Уравнение числовой окружности имеет вид  . тем самым фактически можно получить равенство, связывающее sint и cost.