9. Потенциал поля точечного заряда.

Т.к. напряженность поля точечного заряда убывает с расстоянием, для вычисления потенциала поля предстоит найти работу переменной силы. Для этого вычислим работу по перемещению пробного заряда q вдоль силовой линии на малое расстояние Δr = r₂ − r₁, в пределах которого силу взаимодействия будем считать постоянной и равной

.

Тогда

.

(Перемещение осуществляется вдоль луча, исходящего из заряда Q).

Работу по перемещению заряда из начальной точки, находящейся на расстоянии r до бесконечно удаленной точки найдем путем суммирования элементарных работ ΔA:

= .

Тогда

.

Второй способ требует знания основ интегрального исчисления: работа, совершаемая силами электростатического поля по перемещению пробного заряда q из точки, находящейся на расстоянии r от точечного заряда Q, создающего поле, в бесконечно удаленную точку, вдоль радиальной прямой равна

и потенциал

.

10. Принцип суперпозиции для потенциала.

Рассмотрим электрическое поле, создаваемое системой из n заряженных тел. Это поле можно рассматривать как наложение полей, создаваемых каждым телом в отдельности.

Принцип суперпозиции для потенциалов. Пусть — потенциал результирующего поля

в данной точке, а , 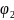. . . , — потенциалы полей каждого из тел. Тогда:

= + + . . .+ (20)

Иными словами, потенциал результирующего поля равен алгебраической сумме потенциалов

полей, создаваемых каждым из тел в отдельности.

Принцип суперпозиции для потенциалов вытекает из формулы и из того факта, что

работа равнодействующей силы есть сумма работ её слагаемых.

11. Связь работы с разностью потенциалов.

К ак следует из закона Кулона, сила, действующая на точечный заряд q в электрическом поле, созданном другими зарядами, является центральной. Напомним, что центральной называется сила, линия действия которой направлена по радиус-вектору, соединяющему некоторую неподвижную точку О (центр поля) с любой точкой траектории. Из «Механики» известно, что все центральные силы являются потенциальными. Работа этих сил не зависит от формы пути перемещения тела, на которое они действуют, и равна нулю по любому замкнутому контуру (пути перемещения). В применении к электростатическому полю (рис.2.10):

.

Рис.2.10. К определению работы сил электростатического поля.

То есть, работа сил поля по перемещению заряда q из точки 1 в точку 2 равна по величине и противоположна по знаку работе по перемещению заряда из точки 2 в точку 1, независимо формы пути перемещения. Следовательно, работа сил поля по перемещению заряда может быть представлена разностью потенциальных энергий заряда в начальной и конечной точках пути перемещения:

.

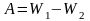Введем потенциал электростатического поля φ, задав его как отношение:

, (размерность в СИ: ).

Тогда работа сил поля по перемещению точечного заряда q из точки 1 в точку 2 будет:

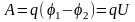
Разность потенциалов 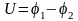называется электрическим напряжением. Размерность напряжения, как и потенциала, [U] = B.

Считается, что на бесконечности электрические поля отсутствуют, и значит . Это позволяет дать определение потенциала как работы, которую нужно совершить, чтобы переместить заряд q = +1 из бесконечности в данную точку пространства. Таким образом, потенциал электрического поля является его энергетической характеристикой