Примеры.

1. Нулевой оператор : , т.е. — собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rⁿ.

2. Тождественный (единичный) оператор I: — т.е. собственное значение тождественного оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rⁿ.

3. Оператор P₂ — оператор проектирования пространства R³ на подпространство R² параллельно вектору : , , т.е. — собственное значение оператора, проектирования, а соответствующие собственные векторы — все ненулевые векторы R³, третья координата которых равна нулю: .

Пусть A— матрица оператора в некотором базисе в Rⁿ.

Собственные значения оператора и соответствующие им собственные векторы связаны соотношением или, что то же самое, :

, . Здесь — единичный оператор.

По теореме о связи координат образа и прообраза имеем: , где E — единичная матрица, а — нулевой вектор Rⁿ .

Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы . Ненулевое решение однородной системы (система нетривиально совместна), существует тогда и только тогда, когда определитель матрицы системы равен нулю: . Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения , а собственные векторы — как решения соответствующих однородных систем.

Легко видеть, что определитель — многочлен n-й степени относительно .

Определение. Уравнение называется характеристическим уравнением оператора, а многочлен — характеристическим многочленом оператора

16 .Скалярное произведение векторов . Условие ортогональности .Скалярное произведение в координатной форме.

Определение

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначаем: , . Поскольку и , то

Условие ортогональности (взаимной перпендикулярности) векторов:

Скалярное произведение векторов в координатах

если векторы и заданы своими координатами в некоторой декартовой системе координат: , , то .

17. Векторное произведение векторов . Условие коллинеарности . Векторное произведение в координатной форме.

Определение

Векторным произведением векторов и (обозначаем его ) называется вектор, который определяется следующим образом:

- , — угол между векторами и ; (определили длину вектора );

- вектор ортогонален вектору и вектору ; (определили положение вектора в пространстве);

- векторы , и образуют правую тройку; (определили направление вектора )

Условие коллинеарности (параллельности или совпадения) векторов

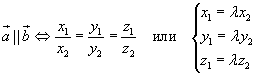
Формула вычисления векторного произведения в координатах

если векторы и заданы своими координатами в некоторой декартовой системе координат: , , то

18. Смешанное произведение векторов Условие компланарности. Смешанное произведение в координатной форме.

Определение

Смешанное произведение векторов , и (обозначаем его ) определяется равенством , т.е. равно скалярному произведению векторов и .

Свойства смешанного произведения

Понятно, что свойства смешанного произведения — это свойства скалярного произведения двух векторов, а поскольку первый из сомножителей, , векторное произведение, то получим суперпозицию свойств векторного и скалярного произведений.

Например: .

Рассмотрим только некоторые, наиболее интересные с нашей точки зрения свойства.

Признак компланарности векторов

Векторы, лежащие в одной плоскости (параллельные одной плоскости) называются компланарными векторами

тогда и только тогда, когда векторы , и компланарны

Действительно, если , то векторы и — ортогональны. Но вектор ортогонален векторам и . Это означает, что у векторов , и есть общий перпендикуляр, а это означает, что векторы , и лежат в одной плоскости (параллельны одной плоскости) — компланарны. Наоборот: если векторы что векторы , и лежат в одной плоскости, то векторное произведение ортогонально этой плоскости, т.е. ортогонально всем векторам плоскости, т.е. ортогонально вектору , т.е. , или, что то же самое, . Что и требовалось доказать.

С помощью смешанного произведения можно вычислять объемы: , V — объем параллелепипеда, построенного на векторах , и как на ребрах. Более того, если , то векторы , и образуют правую тройку, если же то векторы , и образуют левую тройку

Действительно, , где S — площадь основания параллелепипеда, h — высота параллелепипеда, а знак определяется направлением вектора : «+» если вектор образует острый угол с плоскостью векторов , и

«–», если этот угол тупой; , — угол между векторами и .