Структура общего решения неоднородной системы

Вспомним одно из свойств решений линейной неоднородной системы:

Если и — два решения системы , то вектор — решение приведенной однородной системы .

Поскольку выражение задает все решения однородной системы, то для любых двух решений и неоднородной системы справедливо

и, следовательно, выражение позволяет вычислить любое решение неоднородной системы.

Таким образом доказана теорема о структуре общего решения линейной неоднородной системы.

10. Формулы Крамера

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных

Обозначим: 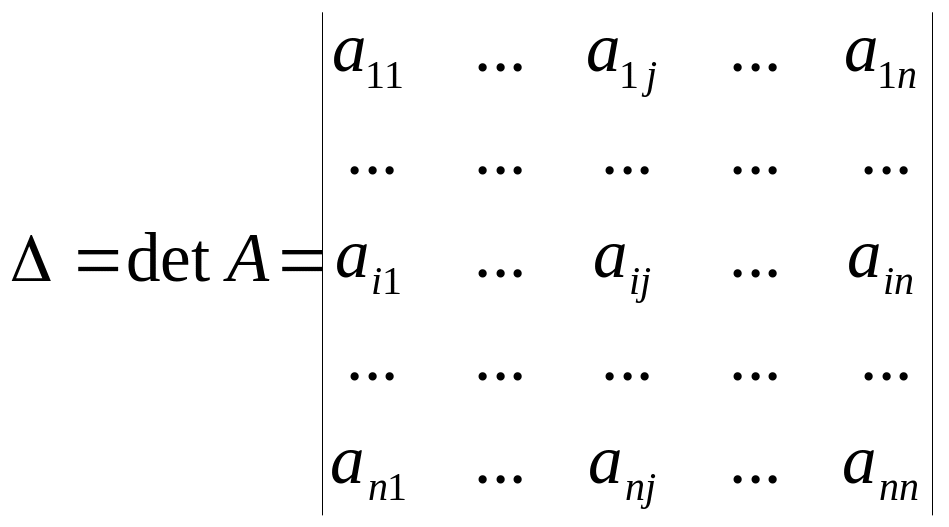— определитель матрицы системы, и — определитель матрицы, полученной из матрицы системы заменой j-го столбца столбцом правых частей.

Если определитель матрицы системы отличен от нуля, , то решение системы

определяется равенствами: .

Докажем это утверждение. Пусть .

Обозначим 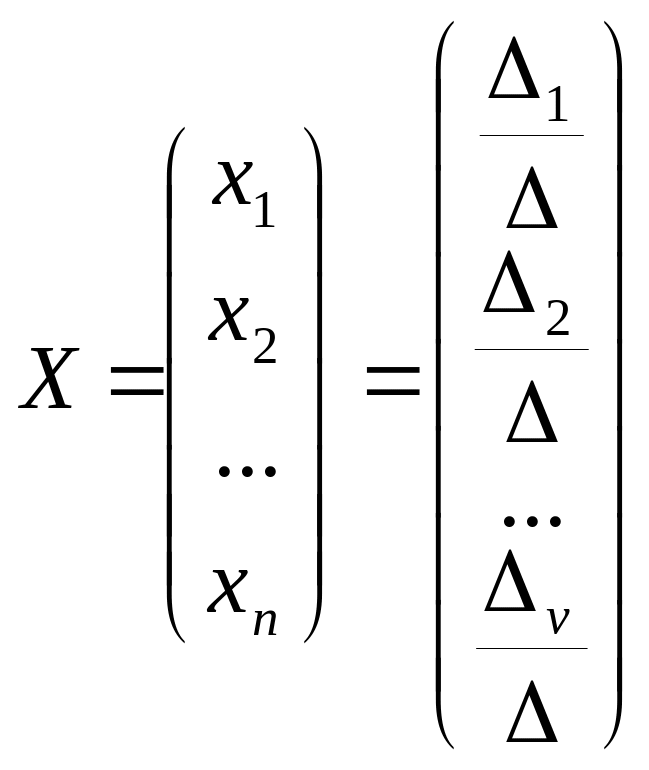и покажем, что Вычислим

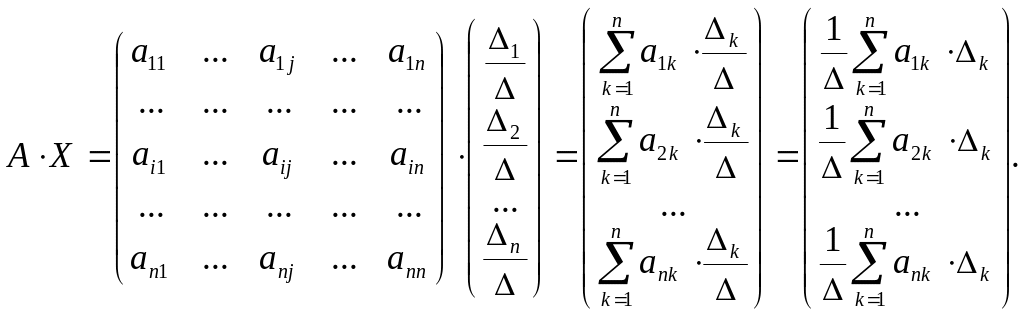
Вычислим определитель разложением по первому столбцу, определитель — по второму, …, — по n-му:

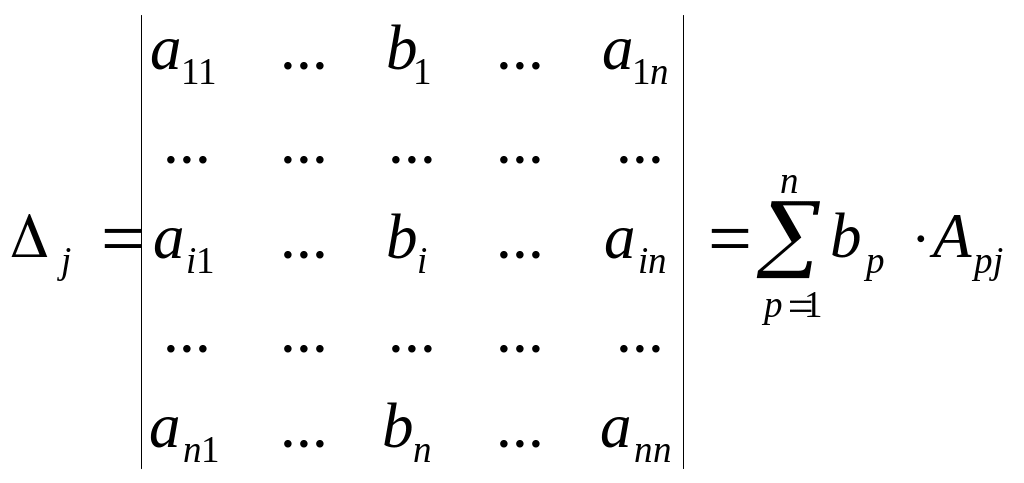, поскольку определитель отличается от только j-м столбцом.

Тогда

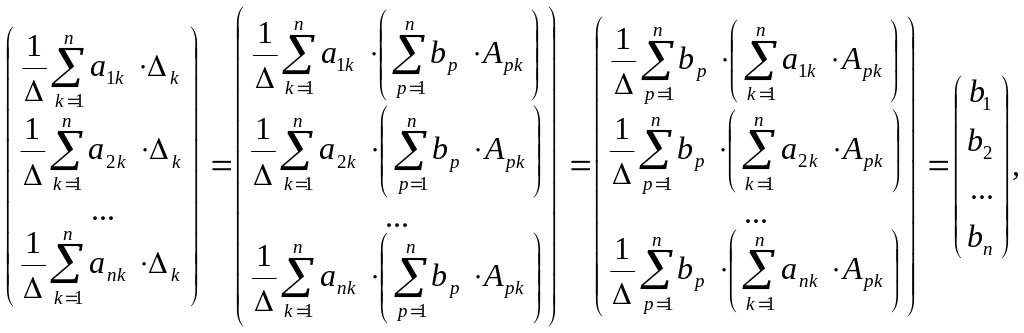
поскольку

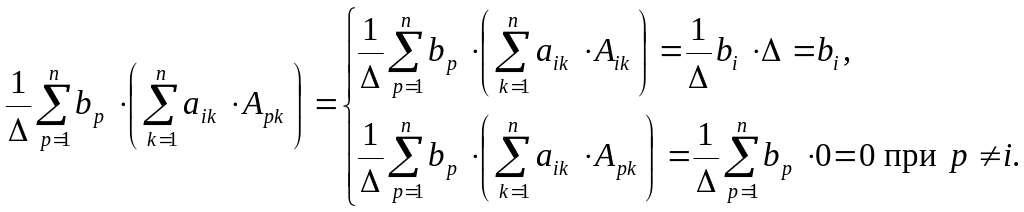
Т.е. 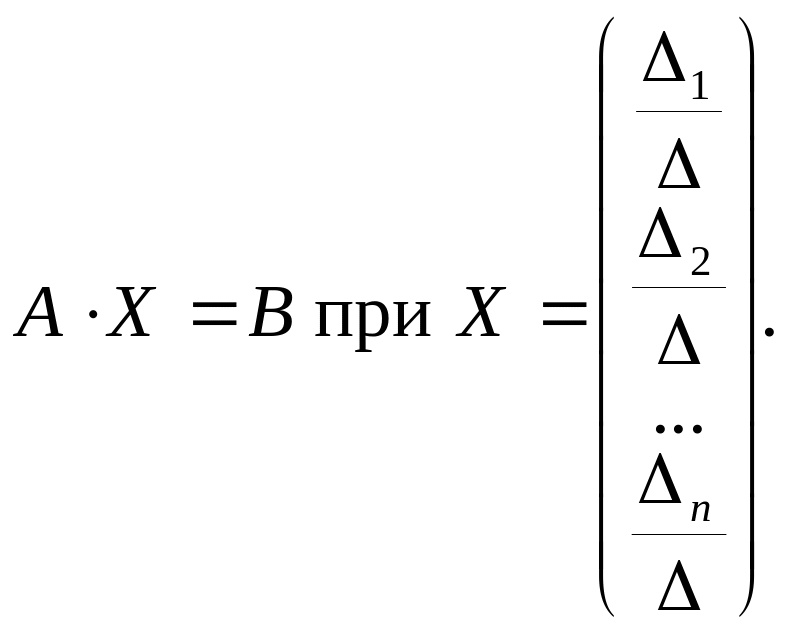Формулы Крамера доказаны.

Замечание. Нетрудно, показать, что выражения и — две формы записи одного и того же равенства.

Действительно,

12. Линейный оператор, Матрица линейного оператора.

Линейный оператор

Определение. Если каждому элементу из пространства Rⁿ ставится в соответствие единственный элемент из пространства R^m , то говорят, что задан оператор, действующий из пространства Rⁿ в пространство R^m (или оператор, действующий в пространстве Rⁿ, если n=m).

Результат действия оператора A на элемент обозначают .

Если элементы и связаны соотношением , то называют образом ; а — прообразом .

Множество элементов пространства Rⁿ, для которых определено действие оператора A, называют областью определения оператора A и обозначают D(A).

Множество элементов пространства R^m, которые являются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A). Если , то

Ядром оператора называется множество элементов линейного пространства Rⁿ, образом которых является нулевой элемент. Ядро оператора обозначают Ker(A): .

Матрица линейного оператора

Определение. Матрица, столбцами которой являются координаты образов базисных векторов некоторого базиса в R^т —

• называется матрицей линейного оператора A в заданных базисах.

Обратите внимание, теперь и в дальнейшем A (полужирная) — обозначение линейного оператора, A(светлая) или A_ef — обозначение матрицы оператора A в некоторых базисах или в базисе и .

Таким образом, доказана следующая теорема.

13.Преобразование координат вектора и матрицы оператора при изменений базиса.

Определение. Матрица называется матрицей перехода от базиса к базису , это матрица, столбцами которой являются координаты базисных векторов («новых» базисных векторов) в базисе (в «старом» базисе).

Матрица перехода обратима. Действительно, ее столбцы линейно независимы, поскольку они — координатные столбцы базисных векторов.

Тогда из имеем формулу преобразования координат вектора при изменении базиса: .

14. Собственные значения и собственные векторы линейного оператора

Определение. Пусть A — линейный оператор, действующий в линейном пространстве Rⁿ. Число называется собственным значением, а ненулевой вектор из Rⁿ — соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением. .

Определение. Пусть A — линейный оператор, действующий в линейном пространстве Rⁿ. Число называется собственным значением, а ненулевой вектор из Rⁿ — соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением. .