4. Обратная матрица .Условие существования обратной матрицы. Единственность обратной матрицы

Обратная матрица

Определение. Если существует квадратная матрица X той же размерности, что и матрица A, удовлетворяющая соотношениям A·X=X·A=E, то матрица A называется обратимой, а матрица X называется обратной к матрице A и обозначается A_­­^-1.

Здесь E — единичная матрица соответствующей размерности.Т.е. A·A_­­^-1= A_­­^-1·A=E.

Пример.

Теорема о существовании обратной матрицы. Если , то матрицаA обратима и

.

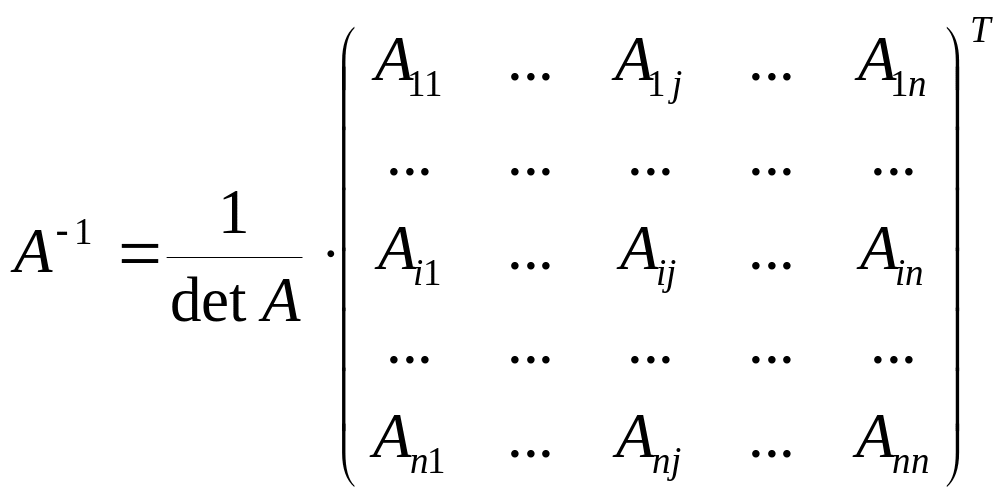Здесь — алгебраическое дополнение элемента матрицы A.

5. Приведение матрицы к ступенчатому виду и гауссовой форме .Линейная зависимость системы столбцов.

Линейная зависимость и линейная независимость в Rⁿ

Определение. Линейной комбинацией векторов называется выражение , где коэффициенты линейной комбинации — некоторые числа.

Определение. Говорят, что вектор пространства Rⁿ линейно выражается через векторы , если его можно представить в виде линейной комбинации этих элементов , т.е. представить в виде .

Определение. Система векторов из Rⁿ называется линейно независимой если из следует равенство нулю всех коэффициентов , .

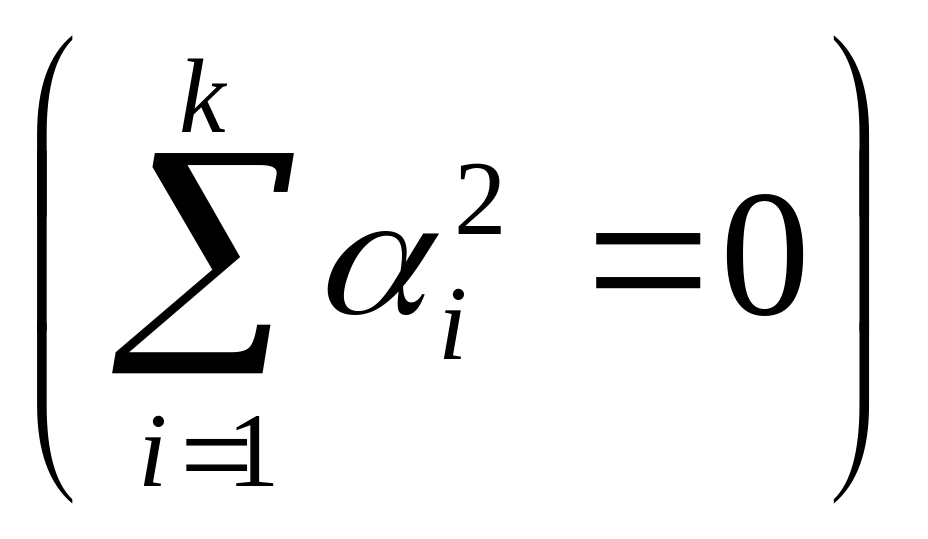Иными словами, линейная комбинация векторов равна нулю тогда и только тогда, когда все коэффициенты линейной комбинации равны нулю.

Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.

Иными словами, существуют такие коэффициенты линейной комбинации , не все равные нулю 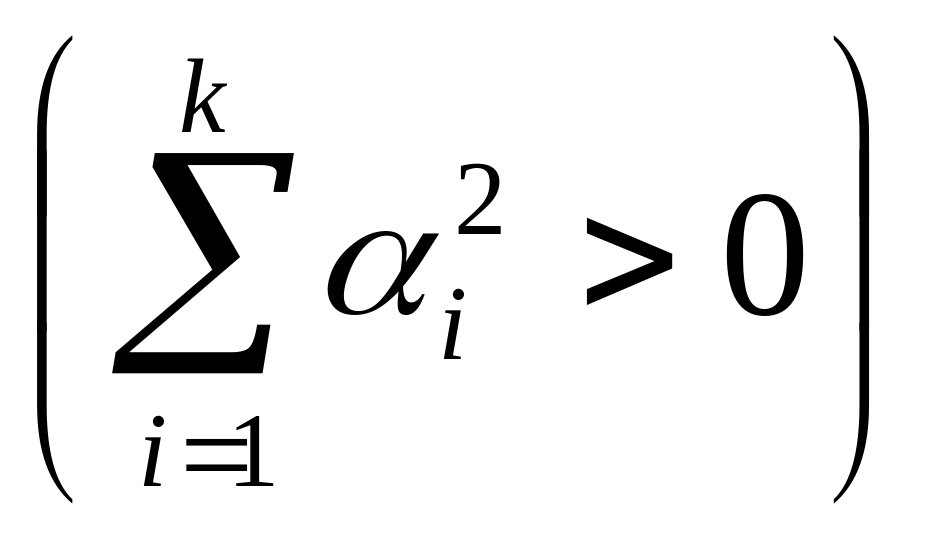, что .

Или: линейная комбинация векторов может обратиться в нуль, хотя не все коэффициенты линейной комбинации равны нулю.

Пример. Исследуем на линейную зависимость векторы из R³.

Составим линейную комбинацию векторов и приравняем ее нулю:

Т.е. линейная комбинация равна нулю тогда и только тогда, когда все ее коэффициенты нулевые — векторы линейно независимы.

Пример. Исследуем на линейную зависимость систему векторов из R³.

Составим линейную комбинацию векторов и приравняем ее нулю:

Пусть, например, , тогда , т.е. существует нулевая линейная комбинация с отличными от нуля коэффициентами — векторы — линейно зависимы.

Приведение матрицы к ступенчатому виду Гауссовым исключением

Утверждение. Любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.

Это утверждение на лекции доказано.

Пример. Приведем к ступенчатой форме матрицу .

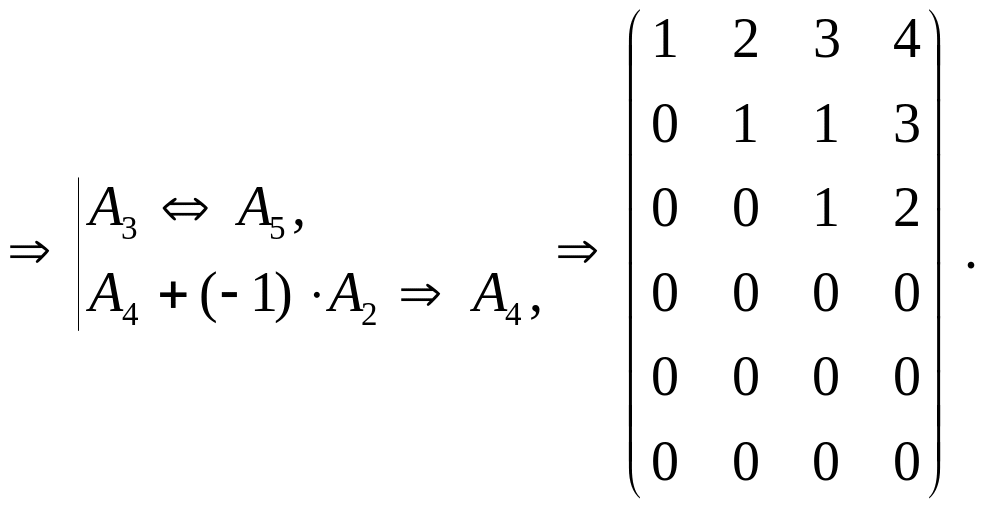
Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют Гауссовым исключением или методом Гаусса

6. Теорема о ранге матриц. Теорема о базисном миноре.

Ранг матрицы

Определение. Ранг матрицы равен максимальному числу линейно независимых строк матрицы. Обозначаем RgA, rgA.

Т.е., если ранг матрицы равен r, то среди строк матрицы есть r линейно независимых строк, а любые r +1 строки — линейно зависимы.

Определение. Матрицы, имеющие одинаковый ранг, называются подобными.

Утверждение. Элементарные преобразования не меняют ранга матрицы.

Базис в Rⁿ. Координаты вектора в заданном базисе. Линейные операции в координатной форме

Определение. Система векторов из Rⁿ образует базис в Rⁿ если:

1. система векторов упорядочена;

2. система векторов линейно независима;

3. любой вектор из Rⁿ линейно выражается через векторы системы.

Иными словами, линейно независимая упорядоченная система векторов

Образует базис в Rⁿ если любой вектор из Rⁿ может быть представлен в виде .

Определение. Выражение называется разложением вектора в базисе , а числа называются координатами вектора в базисе .

Пример. Нетрудно доказать, что система арифметических векторов

линейно независима (см. пример с ) и что для любого из Rⁿ система векторов линейно зависима, поскольку любой вектор линейно выражается через : . Т.е. в Rⁿ существует базис, состоящий из n векторов. Базис называется естественным базисом в Rⁿ, и компоненты вектора — его координаты в естественном базисе.

Справедливо следующее утверждение.

7.Система линейных алгебраических уравнений. Запись в матричной форме. Кронекера-Капелли.

Фундаментальная система решений однородной системы. Структура общего решения однородной системы

Вспомним, что решения однородной системы — векторы из Rⁿ. Вспомним также, что в силу свойств решений линейной однородной системы множество L ее решений — линейное подпространство в Rⁿ. Действительно: если и — два решения однородной системы , то при любых действительных числах α и β вектор — решение системы , иначе говоря, для любых и и любого числах α и . Доказано также, что если ранг r матрицы системы меньше числа неизвестных n, то система имеет ненулевые решения.

Определение. Выражение, позволяющее вычислить все (любое) решения системы, называется общим решением системы.

Теорема (теорема Кронекера-Капелли). Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.

матричная система

Системы линейных алгебраических уравнений. Основные понятия

Рассмотрим систему m линейных алгебраических уравнений относительно n неизвестных :

Определение. Решением системы называется совокупность n значений неизвестных , при подстановке которых все уравнения системы

обращаются в тождества.

8. . Однородная система линейных алгебраических уравнений. Структура общего решения

Теорема о структуре общего решения однородной системы линейных алгебраических уравнений.

Если ранг r матрицы однородной системы линейных уравнений меньше числа неизвестных n, то общее решение системы можно записать в виде линейной комбинации решений фундаментальной системы: .

Пример 1. Исследуем однородную систему линейных алгебраических уравнений

Исследовать однородную систему — ответить на вопрос является ли система нетривиально совместной, и если является, то найти ее общее решение.

Решение. Решим задачу методом Гаусса-Жордана.

Приведем матрицу системы к ступенчатому виду, выполняя элементарные преобразования строк (прямой ход метода Гаусса):

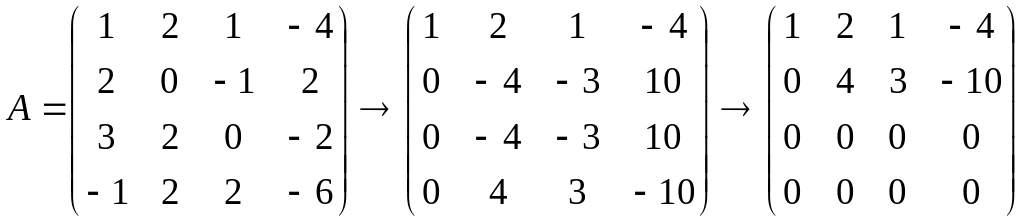
Ранг матрицы системы равен r = 2, число неизвестных n =4, r < n — система нетривиально совместна. Кроме того, очевидно, множества решений исходной системы и системы с преобразованной матрицей совпадают.

Продолжим преобразование матрицы системы, выполняя элементарные операции со строками так, чтобы базисный минор матрицы стал единичным (обратный ход метода Гаусса):

.

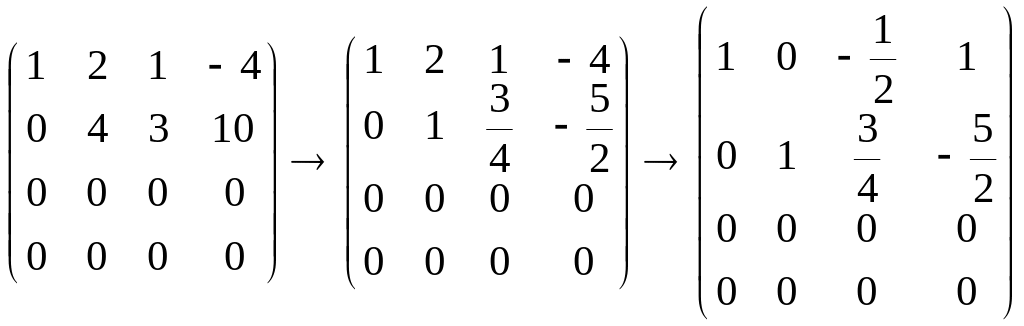Запишем эквивалентную систему уравнений:

Главный минор матрицы этой системы — .

Следовательно, переменные — базисные переменные, а — свободные.

Перенесем свободные переменные вправо:

Получили выражение базисных переменных через свободные. Такое выражение — общее решение однородной системы, записанное «на языке систем».

Найдем базис в подпространстве решений системы (фундаментальную систему). Для этого положим значения свободных переменных равными и вычислим базисные переменные:

Тогда вектор 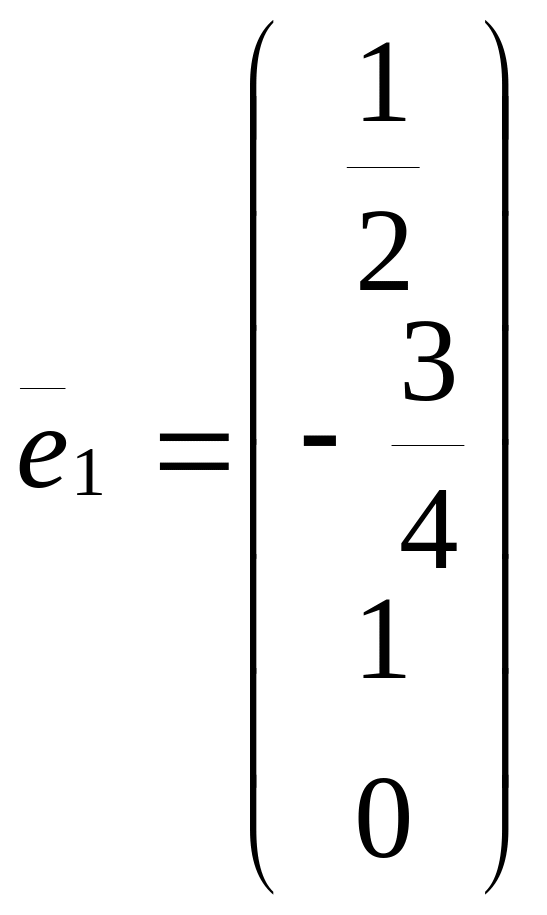— решение однородной системы.

Затем положим значения свободных переменных равными и вычислим базисные переменные:

Тогда вектор — решение однородной системы.

Векторы — линейно независимые решения однородной системы размерность пространства решений которой d = n– r = 4 – 2 = 2, т.е. — базис пространства решений.

Запишем общее решение системы:

.

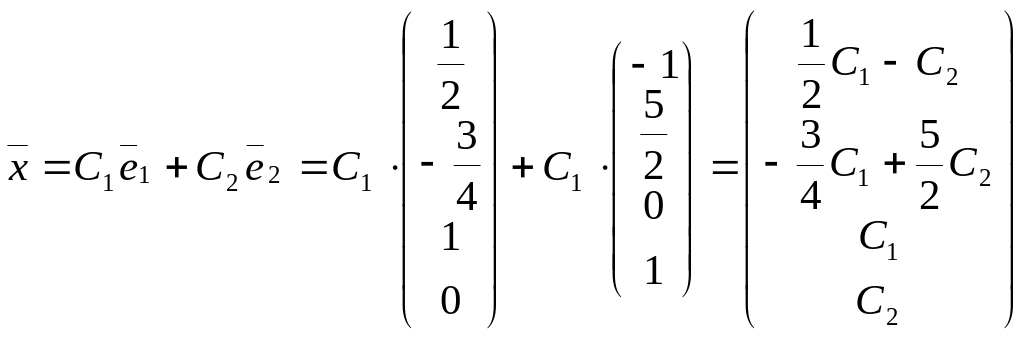9. Неоднородная система линейных алгебраических уравнений. Структура общего решения