
Тема Многомерные случайные величины n 113
Двумерная случайная величина - это:
*A совокупность двух случайных величин , которые принимают значения в результате одного и того же опыта
* совокупность двух случайных событий, которые могут произойти в одном и том же опыте
* совокупность двух случайных величин, которые принимают значения независимо друг от друга
* совокупность двух случайных событий, которые могут произойти независимо друг от друга
Двумерная функция распределения F(x,y) принимает значения
* [-1; 1]
* [0; 2)
* (- ∞; + ∞)
*A [0; 1]
Для двумерной функции распределения F(x,y) имеет место предельное соотношение:
*A
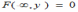
*
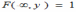
*
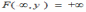
*
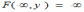
Для двумерной функции распределения F(x,y) имеет место предельное соотношение:
*A

*
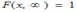
*
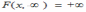
*
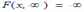
Для двумерной функции распределения F(x,y) имеет место предельное соотношение
*A
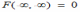
*
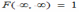
*
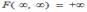
*
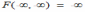
Для двумерной функции распределения F(x,y) имеет место предельное соотношение
*
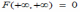
*A
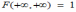
*
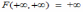
*
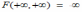
Переход от двумерной функции распределения F(x,y) к одномерной функции распределения F(x) имеет вид:
*A
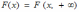
*
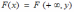
*
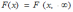
*
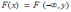
Переход от двумерной функции распределения F(x,y) к одномерной функции распределения F(y) имеет вид
*
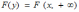
*A

*
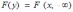
*
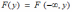
Вероятность попадания значения двумерной случайной величины (Х,Y) в прямоугольную область
*A
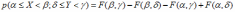
*
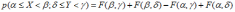
*
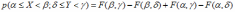
*
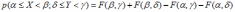
Переход от матрицы распределения двумерной случайной величины (Х,Y) к ряду распределения вероятностей составляющей X имеет вид:
*A
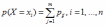
*
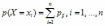
*
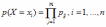
*
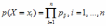
Переход от матрицы распределения двумерной случайной величины (Х,Y) к ряду распределения вероятностей составляющей Y имеет вид:
*
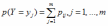
*A
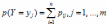
*
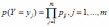
*
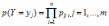
Двумерная плотность распределения f(x,y) принимает значения:
* [-1; 1]
*A [0; + ∞)
* (- ∞; + ∞)
* [0; 1]
Переход от двумерной плотности распределения f(x,y) к двумерной функции распределения F(x,y) имеет вид:
*A
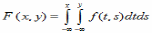
*

*
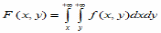
*
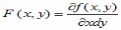
Переход от двумерной плотности распределения f(x,y) к одномерной плотности распределения f(x) имеет вид
*A

*
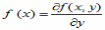
*

*
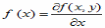
Переход от двумерной плотности распределения f(x,y) к одномерной плотности распределения f(y) имеет вид
*
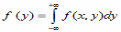
*
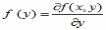
*A
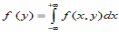
*
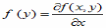
Критерий независимости двух дискретных случайных величин Х и Y имеет вид
*A
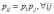
*
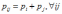
*
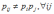
*
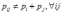
Критерий независимости двух непрерывных случайных величин Х и Y имеет вид:
*A
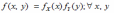
*
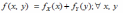
*
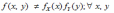
*
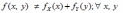
Переход от двумерной плотности распределения f(x,y) к условной плотности распределения f(x/y) имеет вид:
*A
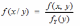
*
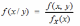
*

*
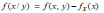
Переход от двумерной плотности распределения f(x,y) к условной плотности распределения f(y/x) имеет вид:
*
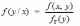
*A
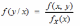
*
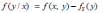
*
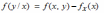
Математическое ожидание компоненты Х двумерной случайной величины (X, Y) равно
*A
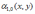
*
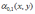
*
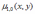
*
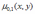
Математическое ожидание компоненты Y двумерной случайной величины (X, Y) равно
*
*A
*
*
Дисперсия компоненты Х двумерной случайной величины (X, Y) равна:
*
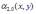
*
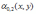
*A
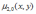
*
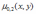
Дисперсия компоненты Y двумерной случайной величины (X, Y) равна
*
*
*
*A
Корреляционный момент KXY двумерной случайной величины (X, Y) равен
*
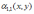
*
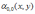
*
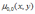
*A
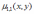
Корреляционный момент KXY случайных величин X, Y принимает значения
* [-1; 1]
*A
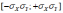
* (- ∞; + ∞)
*
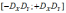
Корреляционный момент KXY независимых случайных величин X, Y равен
* -1
*A 0
* 1
* 0.5
Корреляционный момент KXX равен
* 1
* 0
*A DX
* уX
Коэффициент корреляции RXY случайных величин X, Y принимает значения
*A [-1; 1]
* [0; +∞)
* (- ∞; + ∞)
* [0; 1]
Коэффициент корреляции RXY случайных величин X и Y=5-3Х равен:
*A -1
* 0
* 1
* -3
Коэффициент корреляции RXY случайных величин X и Y=3Х - 5 равен:
* -1
* 0
*A 1
* 3
Регрессия X на y (условное математическое ожидание) mX/y представляет собой
* функцию от x
*A функцию от y
* функцию от x и от y
* константу
Регрессия Y на х (условное математическое ожидание) mY/x представляет собой
*A функцию от x
* функцию от y
* функцию от x и от y
* константу
Какой закон распределения должны иметь случайные величины, чтобы понятия независимости и некоррелированности были равносильны :
*A нормальный
* равномерный
* экспоненциальный
* биномиальный
Композиция двух законов распределения это:
*A закон распределения суммы двух независимых случайных величин
* закон распределения произведения двух независимых случайные величин
* закон распределения суммы двух зависимых случайных величин
* закон распределения произведения двух зависимых случайных величин
n-мерная функция распределения F(x1, x2,... xn) принимает значения
*
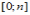
* [0; +∞)
* (- ∞; + ∞)
*A [0; 1]
Функцию распределения F(xi) любой из компонент Хi, входящих в n-мерную случайную величину (Х1, Х2, …Хn) можно получить, если положить все остальные аргументы F(x1, x2,... xn) равными:
*A
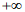
*
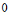
*
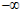
*
n-мерная плотность распределения f(x1, x2,... xn) принимает значения
* [0; n]
*A [0; +∞)
* (- ∞; + ∞)
* [0; 1]
Переход от n-мерной плотности распределения f(x1, x2,... xn) к одномерной плотности распределения fk(xk) имеет вид
*A
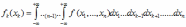
*
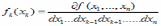
*
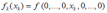
*
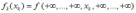
Критерий независимости случайных величин Х1, Х2, …Хn имеет вид
*A
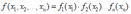
*
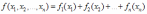
*
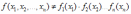
*
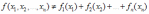
Коэффициент
корреляции Rii
величины
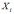 и величины
равен:
и величины
равен:
* Di
* mi
* 0
*A 1
Корреляционный момент Кii величины и величины равен:
*A Di
* mi
* 0
* 1
Для независимых случайных величин Х1, Х2, …Хn корреляционная матрица имеет вид
* все элементы, кроме диагональных, равны 1
*A все элементы, кроме диагональных, равны 0
* все элементы равны 0
* все элементы равны 1
Математическое
ожидание суммы случайных величин
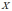 и
и
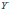 равно:
равно:
*A
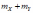
*
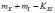
*
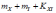
*
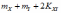
Дисперсия суммы случайных величин и равна:
*
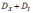
*
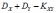
*
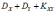
*A

Математическое ожидание произведения случайных величин и равно:
*
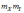
*
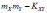
*A
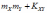
*
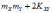
Дисперсия произведения независимых случайных величин и равна:
*
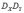
*A
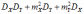
*
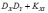
*
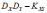
Дисперсия суммы независимых случайных величин и равна:
*A DX+DY
* DX+DY -KXY
* DX+DY +KXY
* DX+DY +2KXY
Математическое ожидание произведения независимых случайных величин и равно
*A mX mY
* mX mY -KXY
* mX mY +KXY
* mX mY +2KXY
Дисперсия произведения независимых центрированных случайных величин и равна
*A DX DY
*
* DX DY +KXY
* DX DY -KXY
Случайные величины X1, X2 имеют следующие числовые характеристики: m1 = 2, m2 = -3, D1 = 1, D2 = 3, K12 = -1. Математическое ожидание величины Y= 6 - 3X1 + 2X2 равно
*A -6
* -7
* 5
* -2
Случайные величины X1, X2 имеют следующие числовые характеристики: m1 = -2, m2 = 3, D1 = 1, D2 = 2, K12 = -1. Математическое ожидание величины Y= 4 - 3X1 + 2X2 равно
*A 16
* 10
* 18
* 13
Случайные величины X1, X2 имеют следующие числовые характеристики: m1 = -1, m2 = 2, D1 = 2, D2 = 3, K12 = -1. Дисперсия величины Y= 2 +3X1 - 2X2 равна
* 24
* 18
* 30
*A 42
Случайные величины X1, X2 имеют следующие числовые характеристики: m1 = -2, m2 = 2, D1 = 3, D2 = 2, K12 = 2. Дисперсия величины Y= 3 - X1 + 2X2 равна
*A 3
* 19
* 18
* 6
Случайные величины X1, X2 имеют следующие числовые характеристики: m1 = -1, m2 = 0, D1 = 3, D2 = 4, K12 = -2. Математическое ожидание величины Y= 4 + X1 X2 равно
* 5
* 0
*A 2
* 3
Случайные величины X1, X2 имеют следующие числовые характеристики: m1 = -1, m2 = 1, D1 = 2, D2 = 3, K12 = -2. Математическое ожидание величины Y= 5 + X1 X2 равно
* 3
*A 2
* 6
* 4
Независимые случайные величины X1, X2 имеют следующие числовые характеристики: m1 = -2, m2 = 2, D1 = 2, D2 = 4. Дисперсия величины Y= 3 + X1 X2 равна
* 16
* 10
* 8
*A 32
Независимые случайные величины X1, X2 имеют следующие числовые характеристики: m1 = 0, m2 = -2, D1 = 3, D2 = 2. Дисперсия величины Y= 1 + X1 X2 равна
* 14
* 12
*A 18
* 6
