Решение уравнения реактора. Цилиндрическая активная зона с бесконечной высотой

Запишем уравнение реактора раскрыв оператор Лапласа:

Если высота бесконечная, то утечки нейтронов нет, то Ф = const, не зависит от z.

Для цилиндра с бесконечной высотой уравнение реактора:

Разделим уравнение на , внеся под знак дифференциала:

Преобразуем уравнение:

Мы можем внести под знак дифференциала, т.к. активная зона однородная, т.е.

не зависит от r.

Умножим уравнение на , внесём под знак дифференциала и введём обозначение

, в результате получим:

Представим решение уравнения в виде бесконечного степенного ряда:

Найдём первую и вторую производные:

Полученные выражения подставим в уравнения:

Это уравнение будет равно 0, если будет равна 0 сумма коэффициентов при одинаковых степенях l:

l^-1 a₁ = 0, не имеет физического смысла, мы его не рассматриваем

Выразим все коэффициенты уравнения через a₀ и a₁:

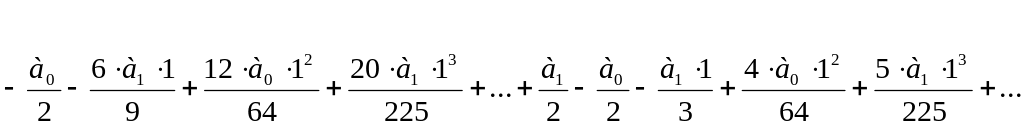
Запишем решение уравнения Ф(l), выразив все коэффициенты через a₀ и a₁:

Сгруппируем слагаемые, содержащие a₀ и a₁:

В результате мы получили, что Ф(l) представляет собой суперпозицию двух асцилирующих функций с убывающей амплитудой:

где J₀ – функция Бесселя 1 рода нулевого порядка, Y₀ – функция Бесселя 2 рода нулевого порядка.

Решение уравнения реактора можно представить в виде:

где .

Полученное решение соответствует бесчисленному множеству задач. Чтобы получить решение для конкретной задачи необходимо применить условие однозначности. Аналогично решается уравнение реактора для цилиндра с ∞ радиусом:

и к этому решению следует применить условие однозначности для конкретной задачи.

Применение условий однозначности при решении уравнения реактора. Условие однозначности

Рассмотрим следующие условия, которые выделяют данную задачу из бесчисленного множества задач:

1. Условие неотрицательности нейтронного потока.

Ф(r, z) ≥ 0

2. Условие граничное (на границе активной зоны (рис.10)):

Ф (R_э) = 0 R_э = R_аз + δ _л

Ф (Н_э) = 0 Н_э = Н_аз + 2 ·δ _л

где δ _л - длина линейной экстраполяции функции Ф .

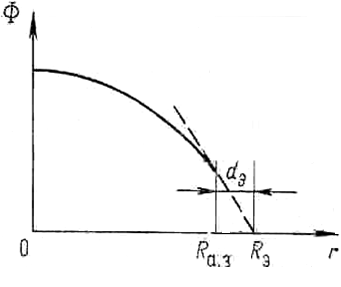
Рис.10. Условие на границе активной зоны

3. Условие симметрии нейтронного потока (рис.11):

d Ф(r) = 0

d r _r=0

d Ф(z) = 0

d z _{z= Наз/2 = Наз/2}

Рис.11. Условие симметрии

Из условия симметрии следует, что нейтронный поток убывает от центра к периферии активной зоны одинаково по всем направлениям.

4. Условие сшивки нейтронных потоков:

Это условие выполняется вследствие большой проникающей способности нейтронов (рис.12).

Ф₁(r_гр) = Ф₂(r_гр)

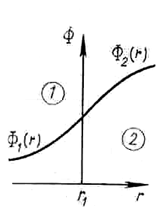
Рис.12. Условие сшивки

5. Условие ограничения нейтронного потока:

Ф(r, z) < ∞