11. Законы трения скольжения. Равновесие при наличии трения скольжения.

1) сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Величина силы трения зависит от активных сил и заключена между нулем и своим максимальным значением, которое достигается в момент выхода тела из положения равновесия (0 ≤ F_тр ≤ F_тр^max );

2) максимальное значение силы трения скольжения не зависит от площади контакта, а определяется величиной нормальной реакции, материалом и состоянием контактирующих поверхностей;

F_тр^max = fN,

где  f – коэффициент трения скольжения, который является безразмерной величиной и зависит от материала и физического состояния трущихся поверхностей, а также от скорости движения тела и удельного давления.

Экспериментально установлено, что  f < f_сц.

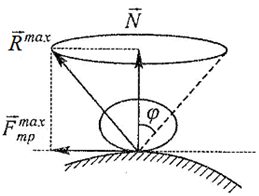
Конус трения – поверхность, образованная линией действия максимальной реакции опорной поверхности при движении тела в различных направлениях.

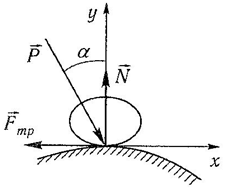
При равновесии тела на шероховатой поверхности под действием силы P  (рисунок 2.3) можно составить два уравнения равновесия:

 ΣF_{kx = 0};  Psinα - F_{тр = 0};

 ΣF_{ky = 0};  - Pcosα + N = 0.

Следовательно,

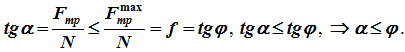
Для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину.

Никакая сила, лежащая внутри конуса трения, не может вывести тело из состояния равновесия.

12. Трение качения. Равновесие при наличии трения качения.

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого. Вследствие деформации тел их касание происходит вдоль площадки AB (рисунок а), появляется распределенная система сил реакции (рисунок б), которая может быть заменена силой и парой (рисунок в).

Сила раскладывается на две составляющие – нормальную и силу трения скольжения. Пара сил называется моментом сопротивления качению  M_c.

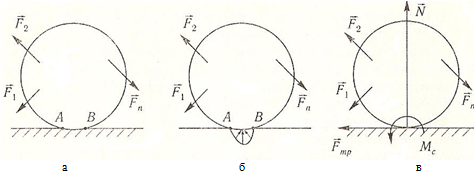
При равновесии тела момент сопротивления качению  определяется из условий равновесия системы сил. При этом установлено, что момент сопротивления принимает значения от нуля до максимального значения. Максимальное значение момента сопротивления, соответствующее началу качения, определяется равенством

 M_c^max = Nδ,

где δ  – коэффициент трения качения, имеет размерность длины [м], зависит от материала контактирующих тел и геометрии зоны контакта.

13. Определение первого и второго статических инвариантов. Частные случаи приведения произвольной системы сил к центру.

14. Теорема Вариньона в векторной и скалярной формах

момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.

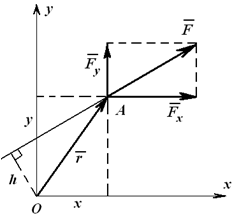
   Например, момент силы F  относительно точки  O можно определить как алгебраическую сумму моментов сил F_x  и  F_y (на которые можно разложить силу F ) относительно той же точки O. То есть

 M_o(F)= -Fh = -F_x y+ F_y x,

где  F_x , F_y ,  x и y  – проекции на оси координат силы F и радиуса-вектора r .