13. Гидравлические сопротивления

Различают два вида гидравлических потерь напора: местные потери и потери на трение по длине. Местные потери напора происходят в так называемых местных гидравлических сопротивлениях, т. е. в местах изменения формы и размеров русла, где поток так или иначе деформируется - расширяется, сужается, искривляется - или имеет место более сложная деформация. Местные потери выражают формулой Вейсбаха

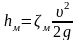(1)

где υ — средняя скорость потока в сечении перед местным сопротивлением (при расширении) или за ним (при сужении) и в тех случаях, когда рассматривают потери напора в гидроарматуре различного назначения; ζ_м - безразмерный коэф­фициент местного сопротивления. Числовое значение коэффициента ζ в основном определя­ется формой местного сопротивления, его геометрическими параметрами, но иногда влияет также число Рейнольдса. Можно считать, что при турбулентном режиме коэффици­енты местных сопротивлений ζ от числа Рейнольдса не зависят и, следовательно, как видно из формулы (1), потеря напора пропорциональна квадрату скорости (квадратичный режим сопротивления). При ламинарном режиме считают, что

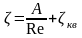(2)

где А — число, определяемое формой местного сопротивления; ζ_кв — коэффициент местного сопротивления на режиме квадратичного сопротивления, т.е. при Re→∞.

Потери напора на трение по длине l определяются общей формулой Дарси

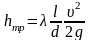(3)

где безразмерный коэффициент сопротивления трения λ опре­деляется в зависимости от режима течения:

при ламинарном режиме λ_л однозначно определяется число Рейнольдса, т. е.

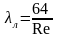
при турбулентном режиме λ_т помимо числа Рейнольдса зависит еще от относительной шероховатости Δ/d, т. е.

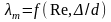
14 Сопротивление по длине.

Потери на трение по длине, - это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и возрастают пропорционально длине трубы .Рассматриваемые потери обусловлены внутренним трением в жидкости, а потому имеют место не только в шероховатых, но и в гладких трубах. Потерю напора на трение можно выразить по общей формуле для гидравлических потерь, т. е.

h_Tp = £_Tp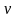 ²/(2g), или в единицах давления

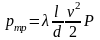
Безразмерный коэффициент наминают коэффициентом потерь на трение по длине, или коэффициентом Дарен. Его можно рас­сматривать как коэффициент пропорциональности между потерей напора на трение, и произведением относительной длины трубы на скоростной напор.

П ри турбулентном течении местные потери напора можно считать пропорциональными скорости (расходу) во второй степени, а коэффициенты потерь £ определяются в основном формой местного сопротивления и практически не зависят от Re,то при ламинарном течении потерю напора следует рассматривать как сумму ,

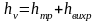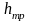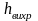где — потеря напора, обусловленная непосредственным действием сил трения (вязкости) в данном местном сопротивлении и пропорциональная вязкости жидкости и скорости в первой степени - потеря, связанная с отрывом потока и вихреобразованием в самом местном сопротивлении или за ним пропорциональная скорости во-второй степени.

Постепенно расширяющаяся труба называется диффузором. Течение жидкости в диффузоре сопровождается уменьшением скорости и увеличением давления, а следовательно, преобразованием кинетиче­ской энергии, жидкости в энергию давления. Частицы движущейся жидкости преодолевают нарастающее давление за счет своей кинетической энергии, которая уменьшается вдоль диффузора и, что особенно важно, в направлении от оси к стенке. Слои жидкости, прилежащие к стоикам, обладают столь малой кинетической' энергией, что иногда оказываются не в состоянии преодолевать повышенное давле­ние, они останавливаются или даже начинают двигаться обратно. Обратное движение (противоток) вызывает отрыв основного потока от стенки и вихреобразования Интенсивность этих явлений возрастает е увеличением угла расширения диффузора а вместе с этим растут и потери на вихреобразование. Полную потерю напора в диффузоре условно рассматриваем как сумму двух слагаемых

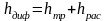
Внезапное сужение русла (трубы) всегда вызывает меньшую потерю энергии, чем внезапное расширение с таким же соотношением площадей. В этом случае потеря обусловлена, во-первых, трением потока при входе в узкую трубу и, во-вторых, потерями на вихреобразование. Последние вызываются тем, что поток не обтекает входной угол, а срывается с него и сужается; кольцевое же пространство вокруг суженной части потока заполняется завихренной жидкостью.