
Отчет по лабораторной работе №1
.docЛабораторная работа №1
Синтез и исследование системы модального управления
двигателем постоянного тока.
I. Цель работы.
Освоение методики синтеза систем управления по состоянию методами модального управления.
II. Теоретическая часть.
Система управления, синтезированная с постоянной u=kx, называется модальной СУ.
Управление идет не по выходной переменной у, как это делается в классических замкнутых системах управления, а по состоянию х.
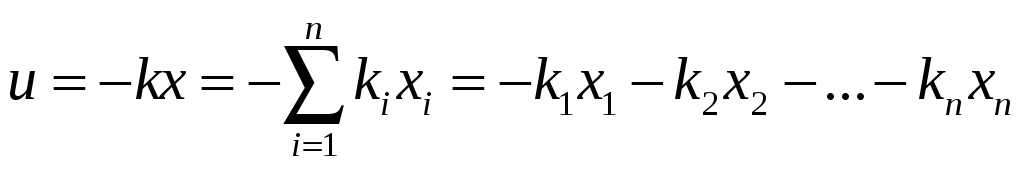
Задача модального управления заключается в определении k.
Матрица k полностью определяет поведение замкнутой системы, при этом порядок системы определяется порядком объекта управления.
Преобразование модели типа «вход – состояние – выход» в пространстве состояний осуществляется при использовании формул перехода в управляемую каноническую форму:
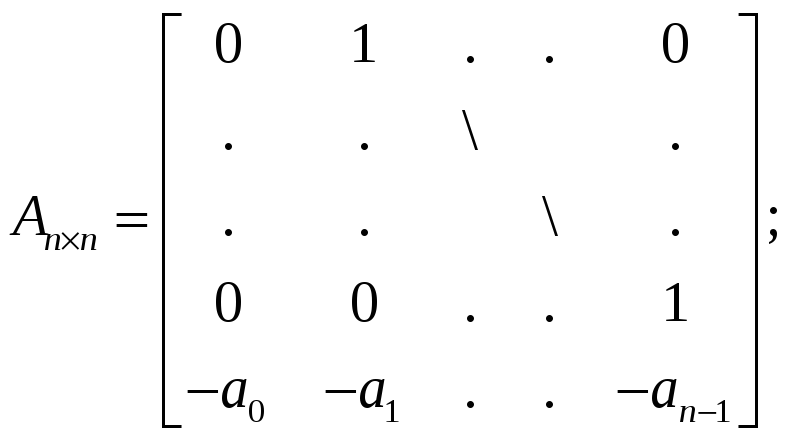
![]()
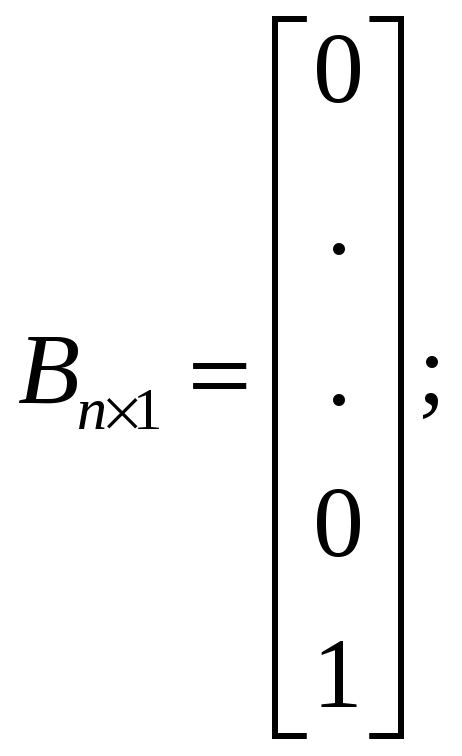
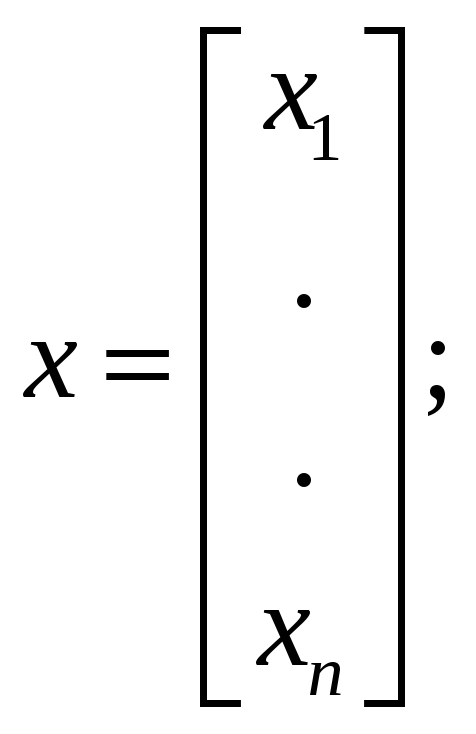
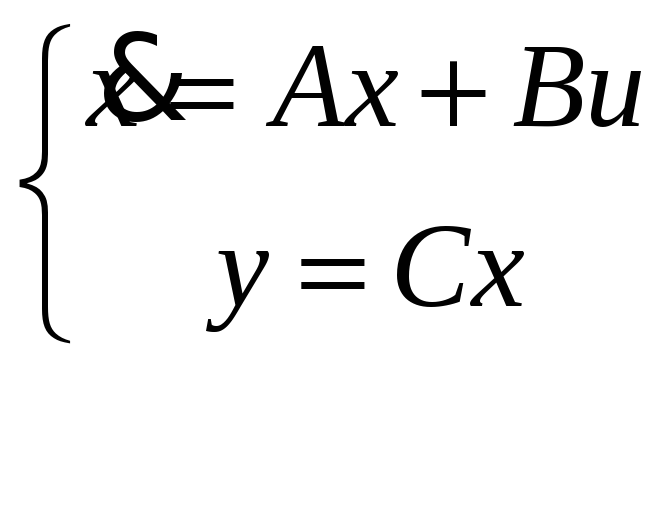 - матричная форма представления
- матричная форма представления
При n=2
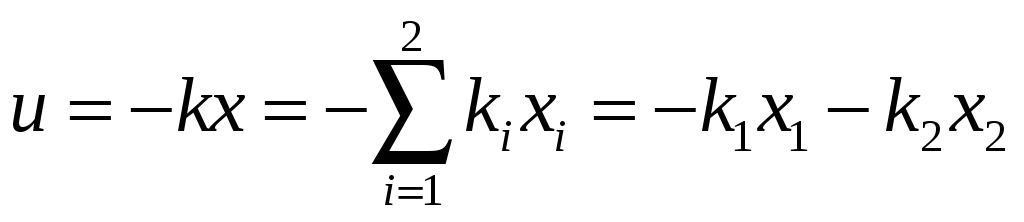
![]()
![]()
![]()
По известной матрице
![]() можно вычислить характеристическое
уравнение замкнутой системы.
можно вычислить характеристическое
уравнение замкнутой системы.
![]()
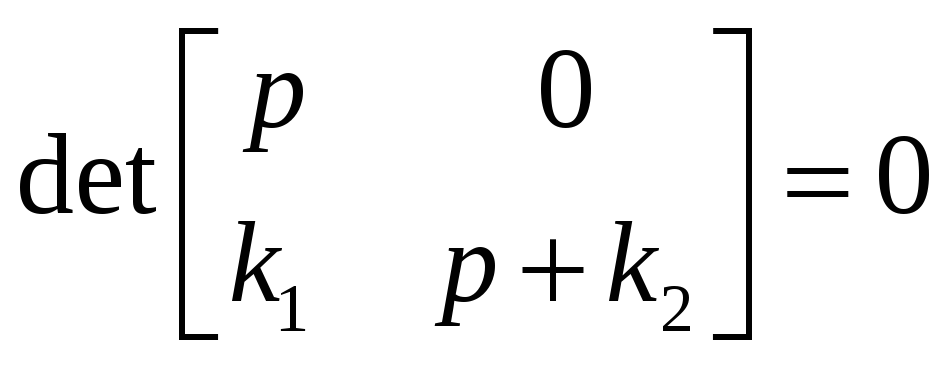
![]() - характеристическое уравнение замкнутой
системы.
- характеристическое уравнение замкнутой
системы.
По желаемому распределению корней определяют вид желаемого полинома. Подобные системы называются системами стабилизации нуль состояния.
Формула Аккермана позволяет получить матрицу К, не прибегая к прямому решению задачи модального направления.
Формула Аккермана осуществляет преобразование объекта, заданного в произвольной форме управления в каноническую форму, и рассчитывают для нее матрицу К и осуществляют преобразование матрицы К к объекту исходного вида.
![]() - формула Аккермана
- формула Аккермана
![]() - матричный полином
- матричный полином
I – единичная матрица.
Методы модального управления в исходной постановке дают приемлимое качество управления.
III. Выполнение работы.
Упрощенная структурная схема обобщенного ОУ, содержащего электродвигатель постоянного тока ЭДПТ и исполнительный элемент ИЭ:
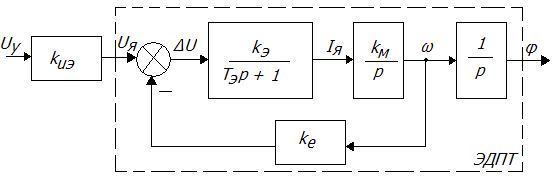

Дано:
|
№ вар |
Параметры синтезируемой СУ |
|
|
|
|
|
|
|
|
|
||||||
|
4 |
0,5 |
8 |
20 |
5 |
0,2 |
1,2 |
0,5 |
tn
– желаемое время переходного процесса
в синтезируемой СУ,
![]() -
перерегулирование.
-
перерегулирование.
1) Рассчитать полную передаточную
функцию обобщенного объекта
![]()
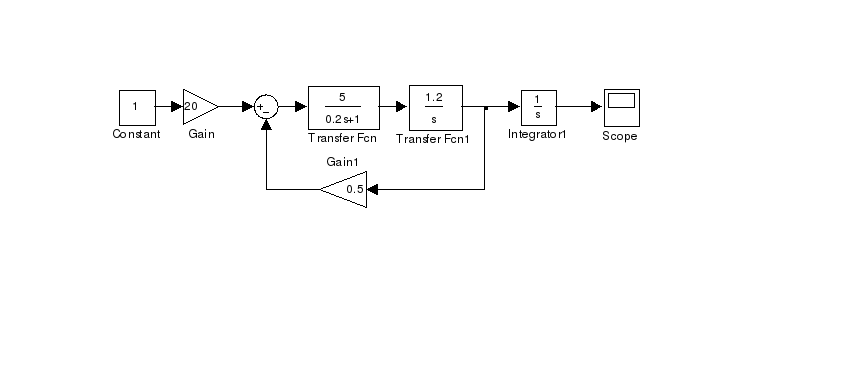
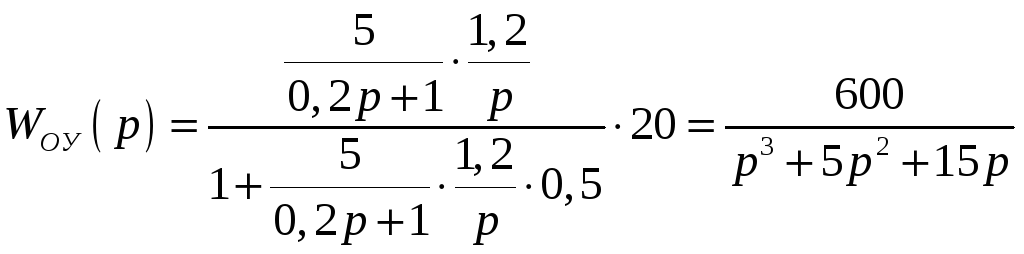
2) Получить характеристическое уравнение ОУ и определить положение полюсов объекта на комплексной плоскости.
Типовые характеристические полиномы обеспечивают типовые переходные функции и могут использоваться при синтезе систем управления методами модального управления.
Полином Беттерворта обеспечивает заданное время переходного процесса и перерегулирование в пределах 15%.
В нашем случае порядок n=3, следовательно
вид полинома:![]() ,
где
,
где
![]() - радиус распределения корней полинома.
Показатели качества соответственно
n=3:
- радиус распределения корней полинома.
Показатели качества соответственно
n=3:
![]() =
6 с – время переходного процесса при
=
6 с – время переходного процесса при
![]() ;
;
![]() - перерегулирование.
- перерегулирование.
Расчет распределения корней полинома
рассчитывается исходя из желаемого
времени регулирования
![]() по формуле
по формуле
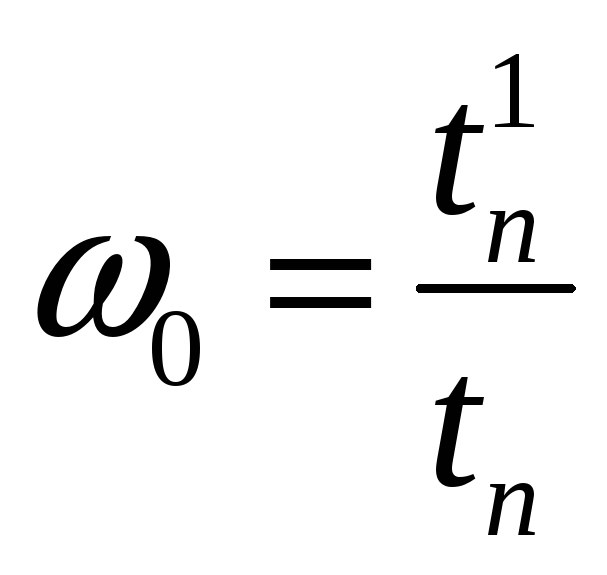 .
.
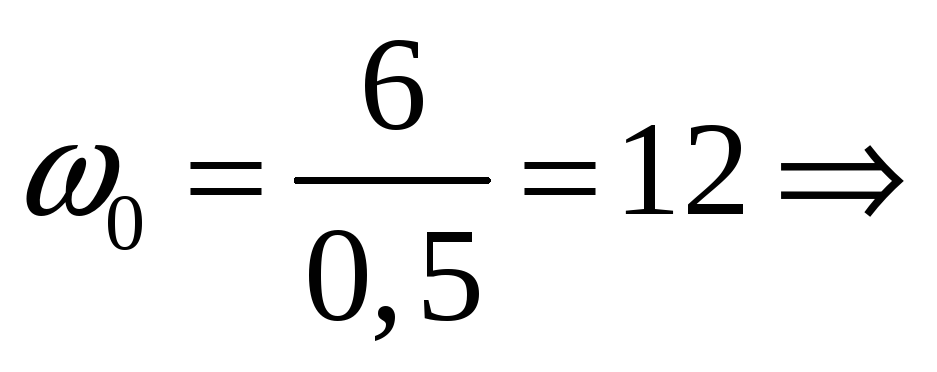 подставляем значение и полином будет
иметь вид:
подставляем значение и полином будет
иметь вид:
![]()
Для расчета корней в Matlab используем функцию roots([коэффициенты полинома]).

3) Преобразовать передаточную функцию
![]() в модель типа «вход – состояние – выход»
(в пространстве состояний), используя
формулы перехода в управляемую
каноническую форму.
в модель типа «вход – состояние – выход»
(в пространстве состояний), используя
формулы перехода в управляемую
каноническую форму.
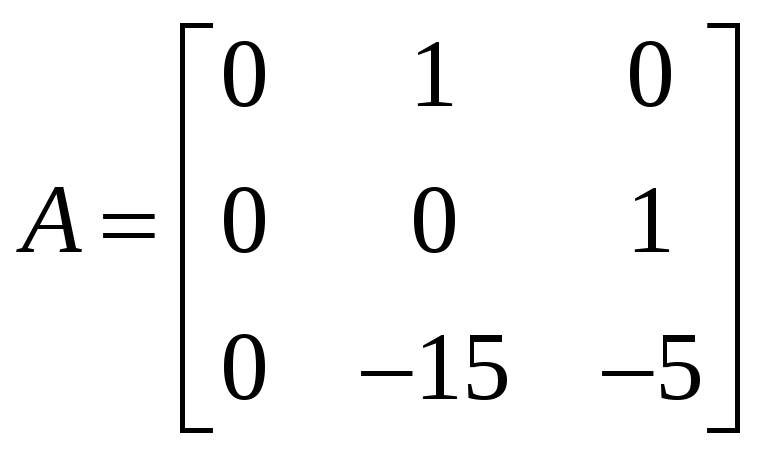
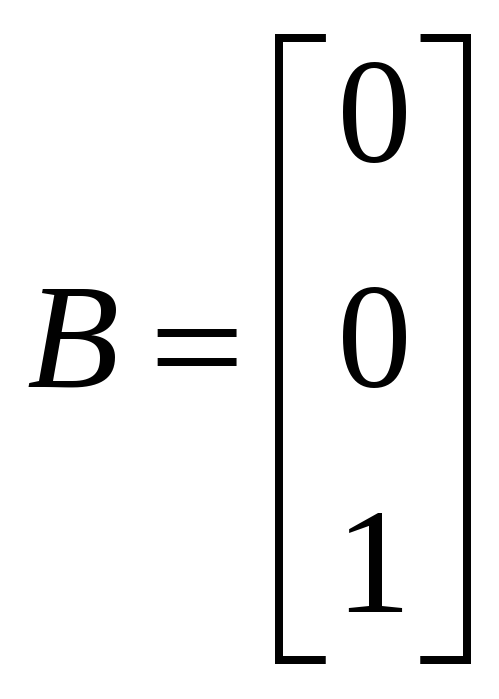
![]()
Пространство состояний:
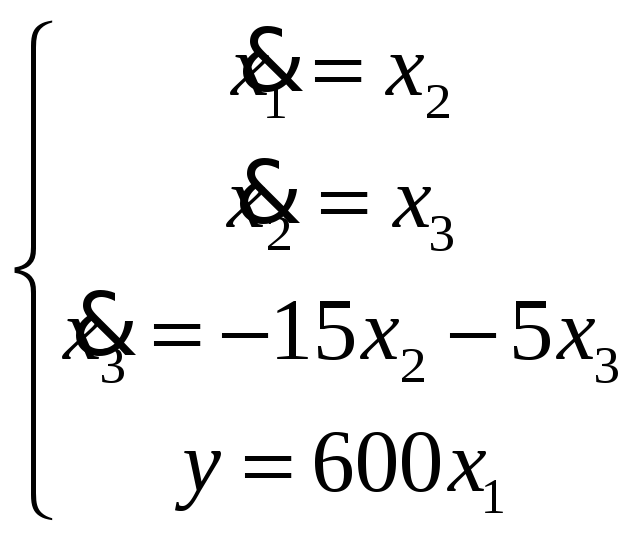
Необходимо получить значение
![]() и
найти составную матрицу
и
найти составную матрицу
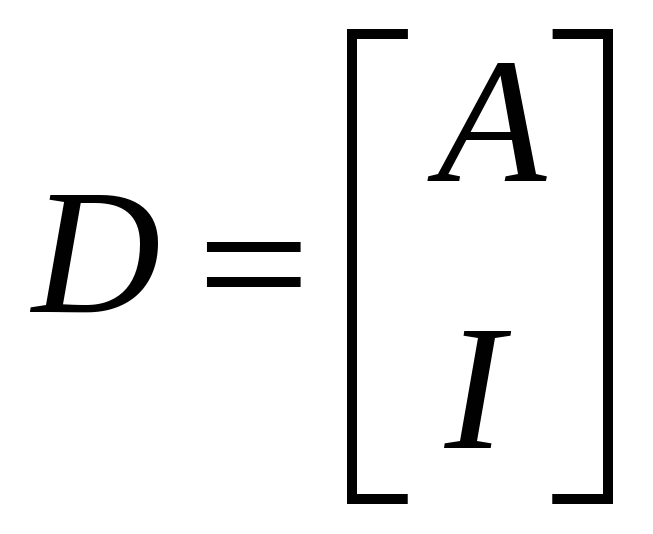 ,
где I – единичная
матрица, соответствующей размерности.
,
где I – единичная
матрица, соответствующей размерности.
Вводим в командном окне Matlab:
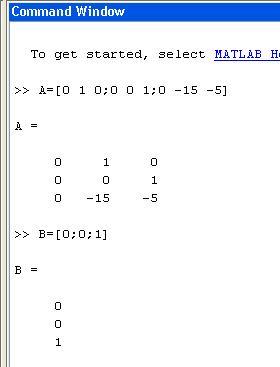
Для получения составной матрицы, в командной строке вводим D=[A;eye(3)] <Enter>.
4) В Simulink набираем исходную схему ОУ и схему, полученную в п.4. В один блок Scope через блок Mux выводим одноименные выходные сигналы схем с учетом того, что они должны совпадать.
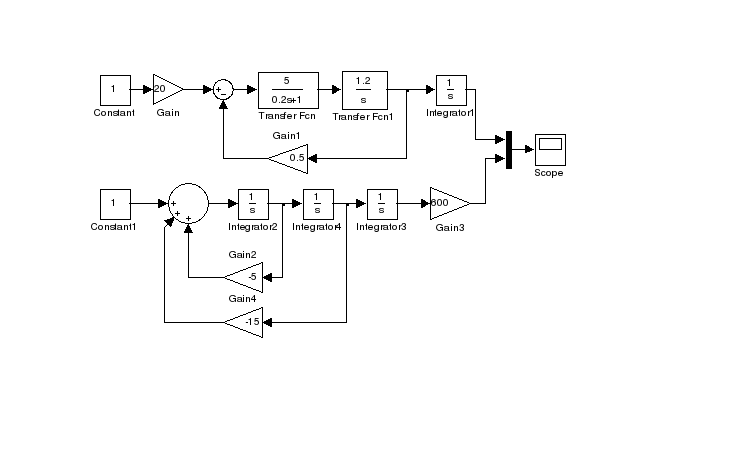
5) Полученный переходный процесс:
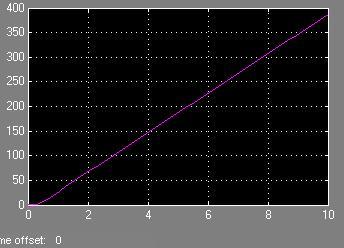
6) Расчет желаемого характеристического
уравнения
![]() синтезируемой
системы.
синтезируемой
системы.
![]() (см пункт 2)
(см пункт 2)
7) Синтез системы стабилизации нуль состояния при нулевом входном сигнале и отсутствии возмущений, определение матрицы К обратной связи по состоянию. Расчет провели по формуле Аккермана:
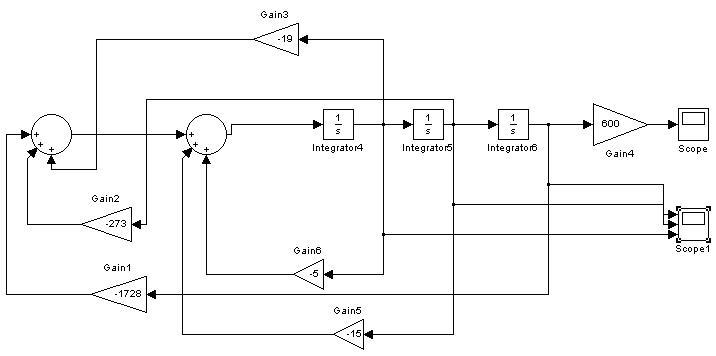
При составлении структурной схемы системы управления используем модель ОУ в пространстве состояний.
8) Зададим начальное условие Initial Condition равное единице и проведем моделирование. Получили фазовые траектории движения системы.
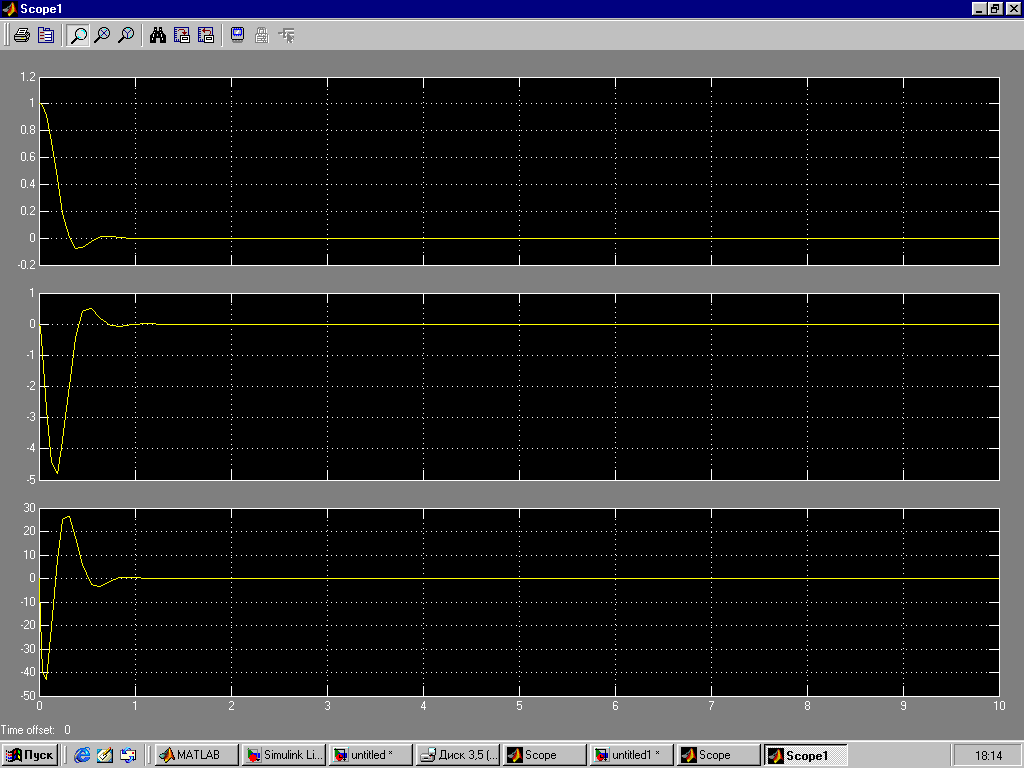
IV. Вывод.
В данной лабораторной работе мы освоили методику синтеза СУ по состоянию методами модального управления; синтезировали систему стабилизации нуль состояния в классическом виде; провели расчет по формуле Аккермана и упрощенной формуле для объектов, заданных в УКФ и убедились в идентичности полученных результатов.
