8. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины
Текущий контроль: в течение первого и второго семестра студенты решают задачи, указанные преподавателем, к каждому практическому занятию. Проводится по одной аудиторной контрольной работе в каждом семестре. Примерные варианты контрольных работ приведены ниже.
Промежуточный контроль: зачет в 1-м семестре проставляется преподавателем по результатам работы студента в течение семестра, выполнению контрольной работы и индивидуальных заданий преподавателя.
Итоговый контроль: экзамен во 2-м семестре предлагается проводить в форме комбинированного устного экзамена по билетам. Каждый билет состоит из 9 вопросов: 1 теоретический вопрос и 8 задач тестового уровня. Каждый вопрос относится к одному из 9 разделов дисциплины. Ответ на теоретический вопрос оценивается в 0,5-1 балл, каждая решенная задача оценивается в 0,5 балла. Таким образом:
оценка «отлично» выставляется студенту, набравшему 4,5-5 баллов;
оценка «хорошо» выставляется студенту, набравшему 3,5-4 балла;
оценка «удовлетворительно» выставляется студенту, набравшему 2,5-3 балла;
оценка «неудовлетворительно» выставляется студенту, набравшему менее 2,5 баллов.
Студент допускается до экзамена после получения зачета по контрольной работе.
Примерный вариант контрольной работы 1 семестра
1 |
ДАНО:
|
|
2 |
Найти
сумму
|
|
3 |
Два однотипных, но различных по качеству продукта продаются в трех магазинах. Матрица А – объемы продаж этих продуктов в 1-м квартале, матрица В – во 2-м квартале (в тыс. руб.). Определить: 1) объемы продаж каждого продукта за два квартала по каждому магазину; 2) объемы продаж каждого продукта за два квартала во всех магазинах; 3) общий объем продаж за два квартала. |
|
4 |
Найти
миноры и алгебраические дополнения
элементов
|
|
5 |
Вычислить
определитель
|
|
,
.
НАЙТИ:
,
.
элементов матрицы
,
и
матрицы
.
6 |
Найти
матрицу, обратную к матрице
|
7 |
Точка В симметрична точке А относительно координатной плоскости yOz. Точка С – проекция точки А на координатную ось Oх.
Найти
координаты точек В
и
С,
если
|
8 |
Найти
координаты вектора
|
9 |
Найти
длину вектора
|
10 |
Найти
скалярное произведение векторов
|
11 |
Найти
угол между векторами
|
12 |
Найти
значение параметра |
13 |
Составить каноническое уравнение прямой, проходящей через точки А(1; 5) и В(-2; 0). Записать параметрическое уравнение этой прямой, общее уравнение прямой. Указать направляющий и нормальный векторы этой прямой. |
14 |
Составить
уравнение прямой, перпендикулярной
плоскости
|
15 |
Решить
методом Крамера и методом Гаусса СЛУ
|
16 |
Найти решение СЛУ, заданной расширенной матрицей системы
|
.
.
Построить чертеж.
,
если
и
,
если
и
.
и
,
если
,
угол между векторами равен 120 градусам.
и
,
при котором векторы
и
ортогональны.
.
.
Примерный вариант контрольной работы 2 семестра
1 |
Заданы
три множества
НАЙТИ:
|
|
2 |
Найти
область определения функции
|
|
3 |
Найти
а)
|
|
4 |
Найти
а) |
|
5 |
Какие
из перечисленных функций являются
бесконечно малыми при
1)
|
|
6 |
Найти пределы функции справа и слева в точке |
а)
|
7 |
Найти точки разрыва функций, если они есть:
а)
|
|
8 |
Найти
наибольшее значение функции
|
|
9 |
Исследовать
кубический полином и построить график:
|
|
10 |
Провести
полное исследование функции
|
|
11 |
Найти
а)
|
|
12 |
Найти
а)
|
|
13 |
Является
ли функция
|
|
14 |
Решить
дифференциальное уравнение
|
|
15 |
Найти
первые частные производные
|
|
16 |
Найти
градиент функции
|
|
,
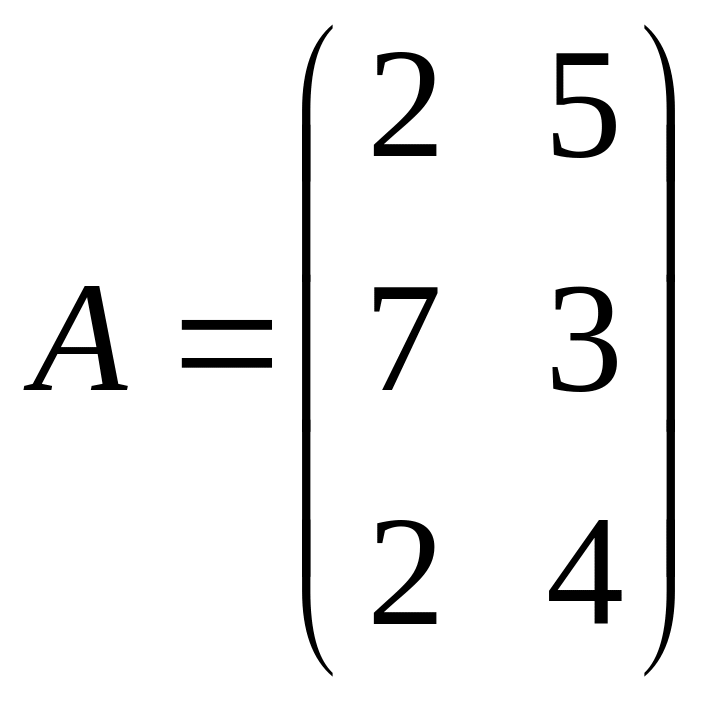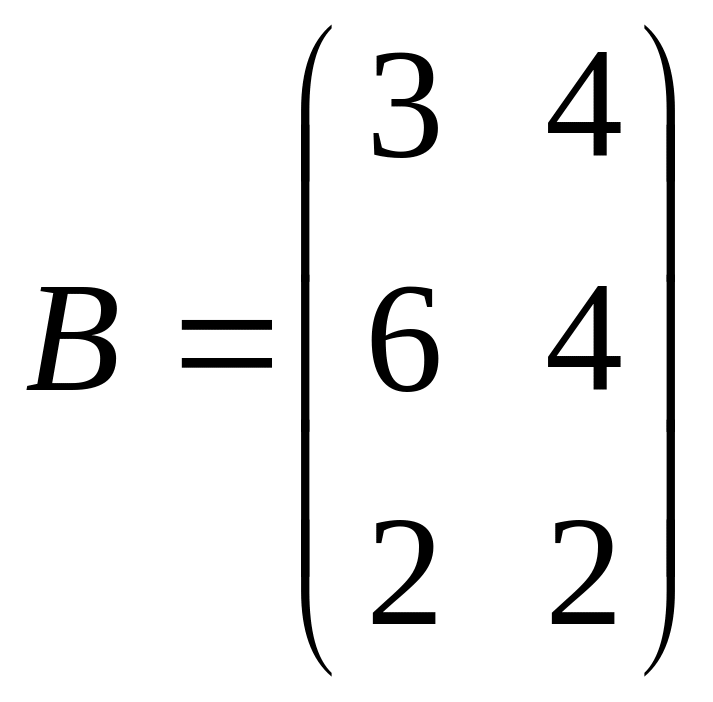
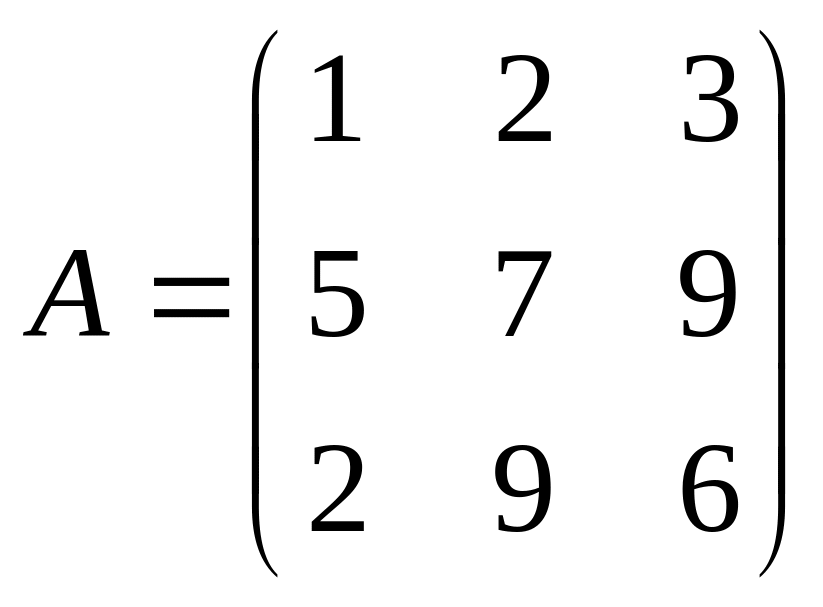
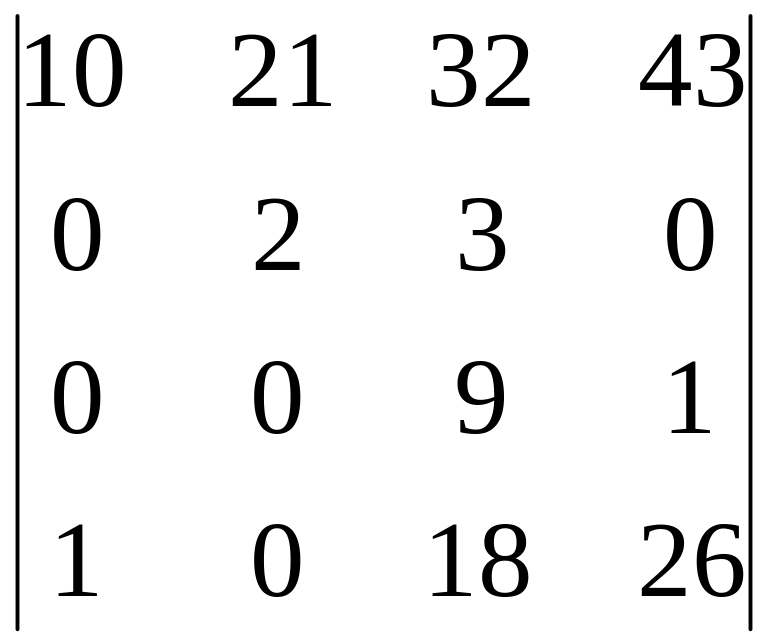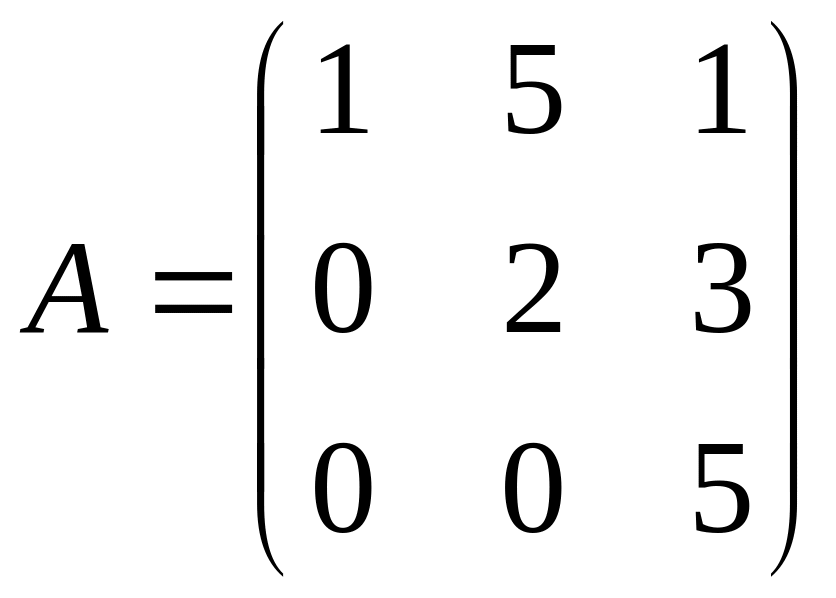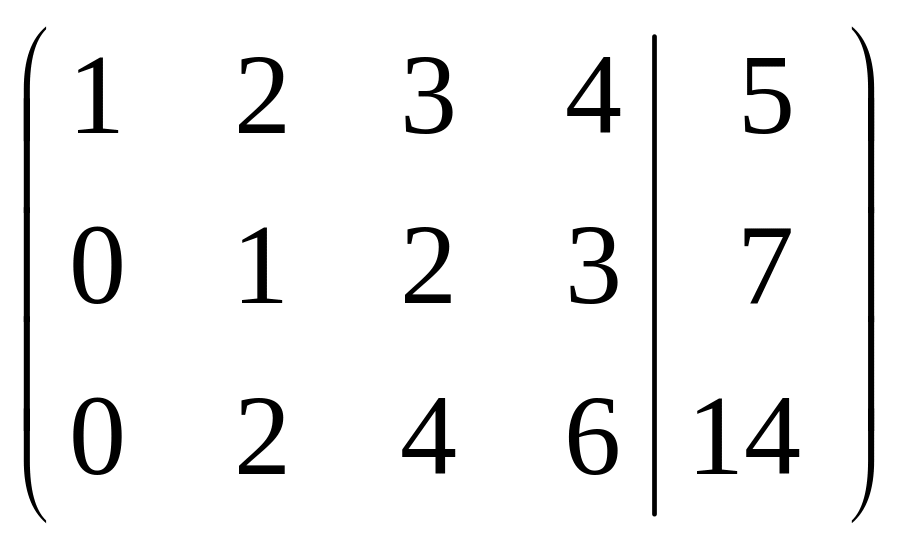и
.
;
;
.
; б)
;
в)
.
;
б)
:
2)
3)
4)
; б)
.
;
б)
;
в)
;
г)
на отрезке
.
.
.
;
б)
.
;
б)
.
решением уравнения
.
.
.
в
точке
.