Многокритериальные задачи линейного программирования, решение методом последовательных уступок.
Задачи многокритериальной, или векторной, оптимизации возникают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (например, стоимость, надежность и т. п.). Требуется найти точку области допустимых решений, которая минимизирует или максимизирует все эти критерии.
Исходные данные:
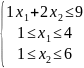
Допустимые уступки:
Формулировка задачи:
Определить переговорное множество, а
затем решить данную задачу методом
последовательных уступок (допустимые
уступки по первым двум критериям принять
равными
Максимизировать
функции (5.1.), (5.2.), (5.3.):
(5.1.)
(5.2.)
(5.3.)
При выполнении условий системы (5.4.)
(5.4.)
И неотрицательности переменных:
(5.5.)
Требуется определить переговорное
множество, а затем решить данную задачу
методом последовательных уступок
(допустимые уступки по первым двум
критериям принять равными
.
Решение задачи
)
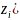– частный критерий;
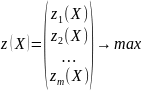
Если критерии на min, их следует привести к max умножением на -1;
Критерии следует ранжировать по степени важности для предприятия;
Назначаются уступки (величина допустимого отклонения
.
Для данной задачи переговорное множество
совпадает с областью допустимых значений,
построенной по системе (5.4). Максимизируем
функцию
при условиях (5.4.). Для этого удобно
воспользоваться графическим методом
(рисунок 5)
Получено решение:
Переходим к максимизации функции
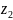при условиях (8.4) и дополнительном
ограничении, учитывающем, что по критерию
нельзя уступать более чем на
.
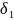Так как
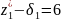, то дополнительное ограничение будет
иметь вид:
6 (5.6.)
Графическое решение задач (5.2.), (5.4.), (5.5.) представлено на рисунке 6.
Получено решение:
Переходим к максимизации функции
при условиях (5.4) и дополнительном
ограничении, учитывающем, что по критерию
нельзя уступать более чем на
.
Так как
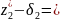7,25
, то дополнительное ограничение будет
иметь вид:
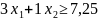(5.7.)
Графическое решение задач (5.2.), (5.4.), (5.5.) и (5.7.) представлено на рисунке (7).
.
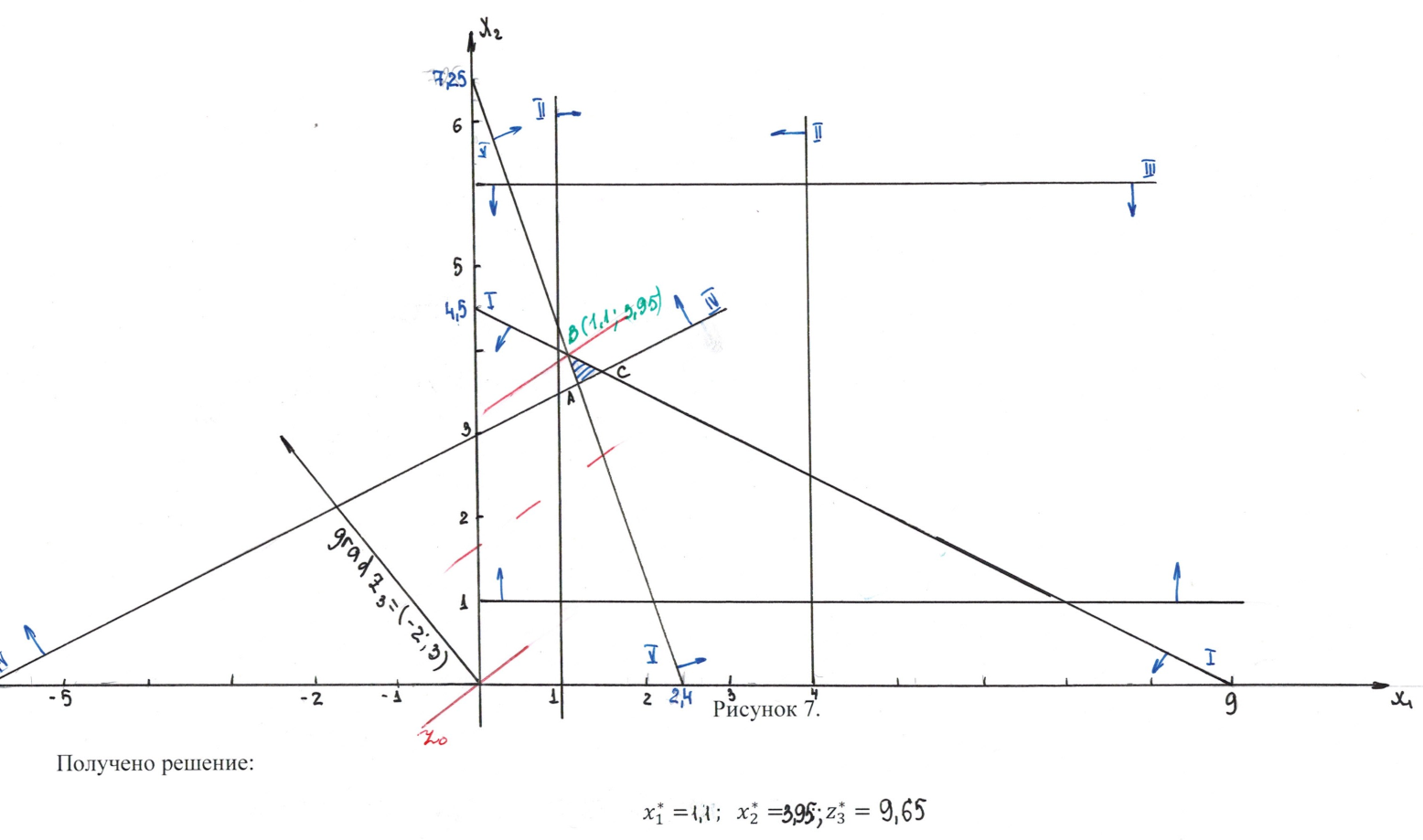
Получено решение:
Получено оптимальное решение многокритериальной задачи:
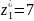
Векторы, действия над ними, линейная зависимость и независимость векторов, их линейная комбинация, базис.
Совокупность n чисел
,
заданных в определенном порядке,
называется n-мерным
вектором. Числа
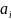– компоненты (координаты) вектора. Число
n – размерность вектора.
Обозначение вектора:
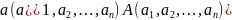
Два n-мерных вектора a и b называются равными, если все их соответствующие компоненты равны:
Сумма двух n-мерных векторов
и
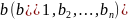есть
вектор
Компоненты которого получаются сложением соответствующих компонентов данных векторов.
Операция сложения векторов обладает свойствами коммутативности и ассоциативности:
a+b = b+a
(a+b)+c = a+(b+c)
Вектор 0(0, 0, …, 0), все компоненты которого равны нулю, называется нуль-вектором. Каков бы ни был вектор а, справедливо равенство а+0=а, т.е. нуль-вектор ведет себя при сложении аналогично числу ноль при арифметике.
Вектор
-
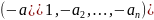противоположный вектору а. обозначается
–а. очевидно, что а+(-а) = 0.
Операция вычитания определяется как сложение с противоположным вектором: a – b = a + (-b)
Произведение вектора
на число λ – вектор
,
компоненты которого получаются умножением
всех компонентов данного вектора на
данное число. Такой вектор обозначается
λа.
Операция умножения вектора на число обладает сочетательным свойством:
λ(ηа) = (λη)а)
и распределительным свойством относительно векторного и числового сомножителей:
(λ+η)а = λа + ηа
λ(а+b) = λa + ηb
при умножении любого вектора на единицу этот вектор не изменится: 1а = а, а при умножении любого вектора на число нуль и любого числа на нуль вектор получается нуль-вектор:
0а = λ0 = 0
Скалярное произведение двух n-мерных векторов а и b – число, равное сумме произведений одноименных координат данных векторов:
Операция скалярного умножения обладает следующими свойствами:
ab = ba
λ(ab) = (λa)b = a(λb)
(a+b)c = ac + bc
aa ≥ 0
система векторов – упорядоченный набор
векторов n-мерного
пространства: S:
Линейная комбинация векторов системы
S с коэффициентами
,
:
.
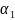Если коэффициенты равны нулю, то такая линейная комбинация называется тривиальной.
,
Если существует ненулевое решение, то система называется линейно-зависимой. Если существует только тривиальное решение системы (1), то система линейно-независима.
Если какой-либо вектор системы линейно выражается через остальные вектора данной системы, то система является линейно-зависимой.
Если система содержит хотя бы один нулевой вектор, то такая система линейно-зависима.
Если количество векторов в системе больше размерности пространства, то система линейно-зависима. (размерность больше числа векторов есть свободные переменные система совместна).
Подсистема данной системы называется подсистемой образующих, если каждый вектор данной системы можно представить в виде линейной комбинации векторов подсистемы.
Базис системы векторов – всякая линейно-зависимая подсистема образующих.
Ранг системы векторов – количество базисных векторов в системе.