
- •Задача линейного программирования, формулировка, математическая модель, алгоритм решения симплексным методом и в Excel. Постоптимизационный анализ решения задачи.
- •Двойственность в линейном программировании. Симметричная пара двойственных задач, правила составления, их экономическое содержание.
- •Двойственные оценки ресурсов и технологий. Математическая модель задачи определения двойственных оценок, их экономическое содержание.
- •Несимметричная пара двойственных задач, правила составления, её особенности.
- •Первая основная теорема двойственности и её экономическая интерпретация.
- •Вторая основная теорема двойственности и её экономическая интерпретация.
- •Третья основная теорема двойственности и её экономическая интерпретация.
- •Задача оптимального пополнения недостающих ресурсов на предприятии.
- •Применение метода динамического программирования при принятии решений об оптимальном распределений инвестиций.
- •Оптимизация плана распределения ресурсов между производственными подразделениями с помощью двойственных оценок при двухуровневой системе управления.
- •Задача целочисленного программирования. Решение методом Гомори, методом ветвей и границ, а также в Excel.
- •Многокритериальные задачи линейного программирования, решение методом последовательных уступок.
- •Векторы, действия над ними, линейная зависимость и независимость векторов, их линейная комбинация, базис.
- •Матрицы, их классификация, алгебра матриц.
- •Определители матриц их свойства и методы вычисления.
- •Метод динамического программирования, принцип оптимальности, параметр состояния, функция состояния, рекуррентные динамические соотношения.
- •Принятие решений в условиях полной неопределённости, матрицы последствий и рисков.
- •Принятие решений в условиях полной неопределённости, правило Вальда.
- •Принятие решений в условиях полной неопределённости, правило Сэвиджа.
- •Принятие решений в условиях полной неопределённости, правило Гурвица.
- •Принятие решений в условиях частичной неопределённости, матрицы последствий и рисков.
- •Принятие решений с помощью дерева решений.
- •Риск как среднее квадратическое отклонение. Бейесовский подход к принятию решений, методы снижения рисков.
- •Матричные игры, основные понятия и определения, решение игры в чистых стратегиях.
- •Теорема об активных стратегиях, решение матричных игр в смешанных стратегиях.
- •Упрощение и геометрическая интерпретация решения матричных игр.
- •Сведение решения игры к решению пары взаимно двойственных задач линейного программирования.
- •Некооперативные биматричные игры, основные понятия и определения. Анализ биматричной игры в некооперативном варианте.
- •Кооперативные биматричные игры, оптимальность по Парето, переговорное множество, арбитражные схемы Нэша, функция Нэша.
- •Экспертные методы принятия решений.
Задача целочисленного программирования. Решение методом Гомори, методом ветвей и границ, а также в Excel.
Модель задачи:
Найти производственную программу
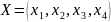 ,
максимизирующую целевую функцию прибыли:
,
максимизирующую целевую функцию прибыли:
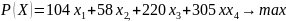 (1)
(1)
при ограничениях по ресурсам:
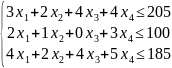 (2)
(2)
И при условиях неотрицательности переменных:
. (3.)
Решение
Последняя таблица:
|
Б |
Н |
|
|
|
|
|
|
|
|
|
0 |
|
53,33 |
-0,33 |
0,33 |
0,00 |
0,00 |
1,00 |
0,33 |
-1,00 |
|
|
0 |
|
33,33 |
0,67 |
0,33 |
0,00 |
1,00 |
0,00 |
0,33 |
0,00 |
|
|
0 |
|
4,58 |
1,67 |
0,08 |
1,00 |
0,00 |
0,00 |
-0,42 |
0,25 |
|
|
|
|
11175,00 |
136,00 |
62,00 |
0,00 |
0,00 |
0,00 |
55,00 |
0,00 |
|
|
Отрицательных двойственных оценок нет, следовательно, получен оптимальный план:
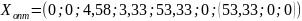
И максимальная прибыль составляет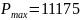 ед.
ед.
Не выполняется условие целочисленности решения: элементы базисного плана нецелочисленны.
Метод Гомори. Нахождение решения задачи целочисленного программирования методом Гомори начинают с определения симплексным методом оптимального плана задачи без учета целочисленности переменных. После того как этот план найден, просматривают его компоненты. Если среди компонентjd нет дробных чисел, то найденный план является оптимальным планом задачи целочисленного программирования (1)-(3) Если же в оптимальном плане задачи переменная принимает дробное значение, то к системе уравнений (2) добавляют неравенство
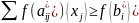 (4)
(4)
и находят решение задачи (1) – (3), (4).
В неравенстве (4)
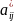 и
и
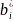 –
преобразованные исходные величины
–
преобразованные исходные величины
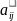 и
и
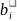 ,
значения которых взяты из последней
симплекс–таблицы, а
,
значения которых взяты из последней
симплекс–таблицы, а
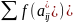 и
и
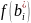 –
дробные части чисел (под дробной частью
некоторого числа а понимается наименьшее
неотрицательное число b такое, что
разность между а и b есть целое). Если в
оптимальном плане задачи (1) – (3) дробные
значения принимают несколько переменных,
то дополнительное неравенство (4)
определяется наибольшей дробной частью.
–
дробные части чисел (под дробной частью
некоторого числа а понимается наименьшее
неотрицательное число b такое, что
разность между а и b есть целое). Если в
оптимальном плане задачи (1) – (3) дробные
значения принимают несколько переменных,
то дополнительное неравенство (4)
определяется наибольшей дробной частью.
Если в найденном плане задачи (1) – (3), (4) переменные принимают дробные значения, то снова добавляют одно дополнительное ограничение и процесс вычислений повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования (1) – (3), либо устанавливают ее неразрешимость.
Метод «ветвей и границ».
Рассмотрим задачу с двумя переменными, вошедшими в базис, и решим ее методом «ветвей и границ» для поиска целочисленного решения.
 (1)
(1)
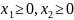 (2)
(2)
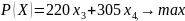 (3)
(3)
Системы уравнений (1) и (2) определяют область допустимых значений ОАВС, где координаты вершины В определяют оптимальный план производства.
В = (4,58; 33,3)
Переменная
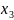 в оптимальном плане не является целой,
следовательно, относительно нее будет
производится ветвление.
в оптимальном плане не является целой,
следовательно, относительно нее будет
производится ветвление.
Процесс ветвления делит исходную задачу
на две подзадачи а) и б). Одна из них
отличается добавлением условия
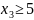 ,
во второй подзадаче добавляется условие
,
во второй подзадаче добавляется условие
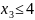 .
При этом из области ОАВС исключается
подобласть
.
При этом из области ОАВС исключается
подобласть
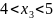 .
.
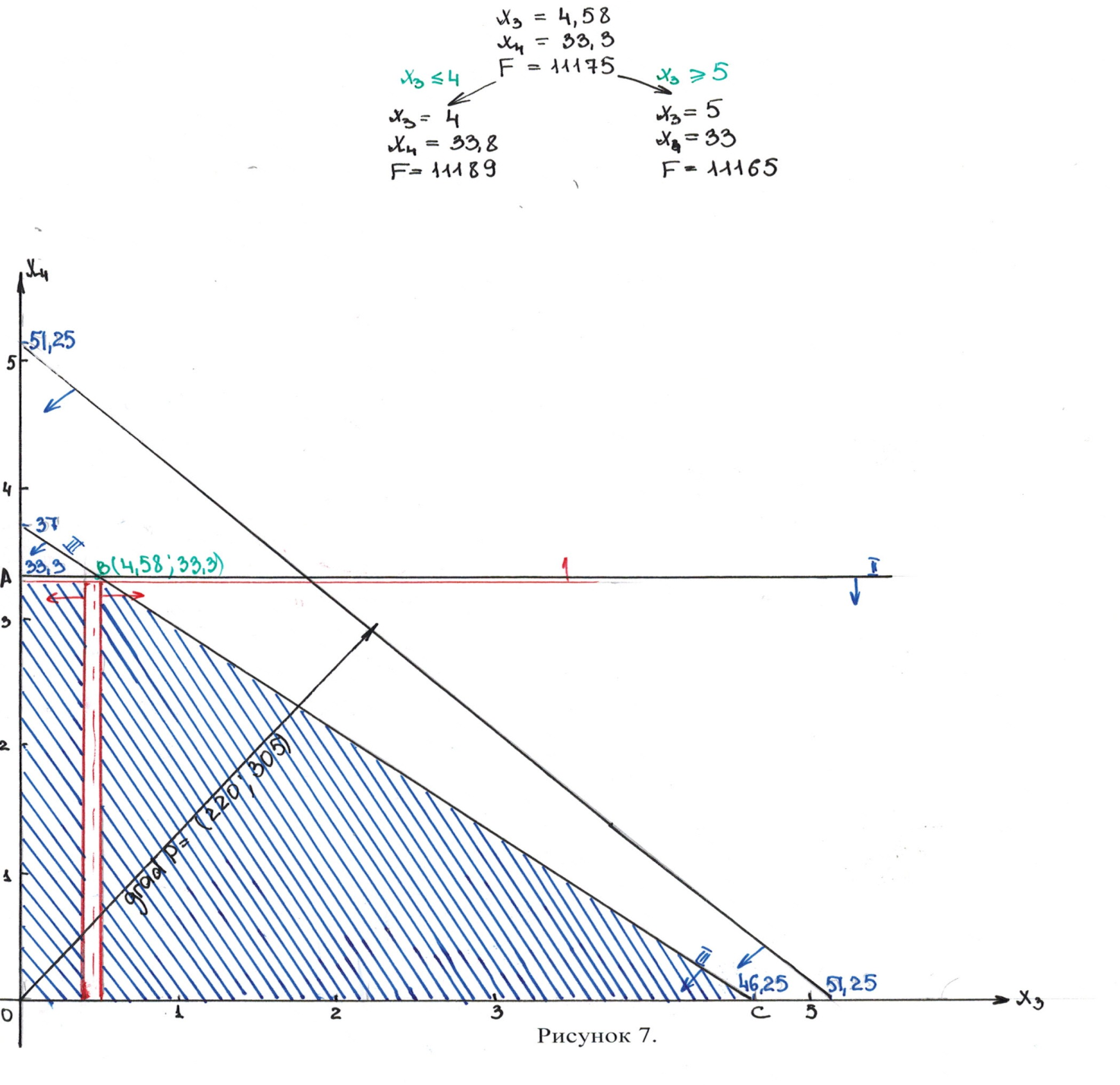
В результате преобразований получен оптимальный целочисленный план производства:
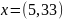
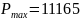
Решение в Excel
(см. №1)
Для проверки решения в программе Excel с помощью средств «Поиск решений» при описании ограничений необходимо учесть условия целочисленности для изменяемых ячеек – т.е. указать, что изменяемые ячейки (план выпуска) могут быть только целыми числами.
