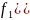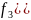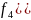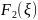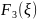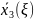7. Третья основная теорема двойственности и её экономическая интерпретация.

Значения переменных в оптимальном решении двойственной задачи представляют собой оценки влияния правых частей , системы ограничений исходной задачи на величину максимума ее ценовой функции:

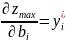
Т.о., увеличение правой части i-го ограничения приводит к увеличению или уменьшению в зависимости от того, будет ли положительным или отрицательным. При этом скорость изменения определяется величиной .

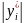Экономическое содержание:

Двойственные оценки ресурса – это приращение прибыли, приходящееся на единицу приращения этого ресурса. Речь идет о достаточно малых приращениях, т.к. изменение величины в некоторый момент вызовет изменение оценок .

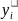8. Задача оптимального пополнения недостающих ресурсов на предприятии.

Если при выполнении оптимального плана какие-либо ресурсы используются полностью, они образуют «узкие места производства», т.е. их нужно заказать дополнительно.

Математическая модель

Найти вектор , максимизирующий суммарный прирост прибыли

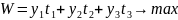(3.1.)

при условии сохранения двойственных оценок ресурсов и структуры производственной программы (по примеру):

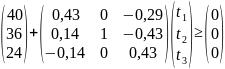(3.2.)

- оптимальный план исходной задачи

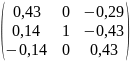- коэффициенты при дополнительных переменных

Решение

Пусть – вектор дополнительных объемов ресурсов. Для решения будут использоваться найденные ранее двойственные оценки, следовательно, должно выполняться равенство:

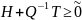(3.4.)

Т.к. «узкими местами производства» являются только первый и третий ресурсы, а второй ресурс находится в избытке, то задача состоит в том, чтобы найти вектор 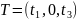, максимизирующий суммарный прирост прибыли:

Для дальнейшего решения неравенства (3.3.) и (3.3.) следует переписать в виде систем:

(3.5.) 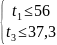(3.6.)

Получена задача линейного программирования: максимизировать функцию (3.1.) при условиях (3.5.), (3.6.) и (3.4.).

Т.к. задача имеет только две переменные, ее можно решить графически.

9. Применение метода динамического программирования при принятии решений об оптимальном распределений инвестиций.

Задача динамического программирования – многошаговый процесс принятия решений. На каждом шаге определяется экстремум функции только одной переменной.

Задача о распределении капитальных вложений. Указано n пунктов, где требуется построить или реконструировать предприятия одной отрасли, для чего выделено b рублей. – прирост мощности на i-том предприятии, если оно получит 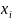капитальных вложений. Требуется найти распределение

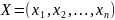
Максимизирующее суммарный прирост мощности/прибыли.

Исходные данные:

Таблица 1.Исходные данные

	0	100	200	300	400	500	600	700
	0	20	20	30	38	43	49	52
	0	13	25	37	47	55	61	66
	0	6	13	20	27	33	38	41
	0	24	36	42	46	48	48	49

Формулировка задачи:

Производственное объединение состоит их четырех предприятий (n=4). Общая сумма капитальных вложений составляет 700 тыс. руб. (b=700), выделяемые предприятиям суммы кратны 100 тыс. руб. Значения функций 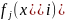приведены в таблице 1. Например, число 49 в первой строке означает, что если третье предприятие получит 600 тыс. руб., капитальных вложений, то прирост прибыли на этом предприятии составит 49 тыс. руб. и т.д.

Найти такой вариант распределения средств капитальных вложений, чтобы прирост прибыли был максимален.

Математическая модель задачи

Примем следующие обозначения:

• n – количество пунктов, где требуется построить или реконструировать предприятия одной отрасли;

• b – общая сумма выделенных средств;

• – количество капитальных вложений, полученных i-тым предприятием;

• – прирост мощности прибыли на i-том предприятии, если оно получит i-e предприятие;

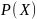• – прирост мощности (прибыли)

Требуется найти такое распределение 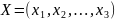капитальных вложений между предприятиями, которое максимизирует прирост мощности или прибыли:

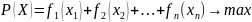(1.1.)

при ограничении по общей сумме капитальных вложений

,

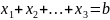при этом будем считать, что все переменные принимают только целые неотрицательные значения.

Решение

Введем параметр 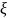состояния – количество средств, выделяемых нескольким предприятиям, и определим функцию состояния 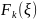– максимальную прибыль на первых k предприятиях, если они вместе получают руб.

Если из рублей k-е предприятие получит рублей, то каково бы ни было это значение, оставшиеся (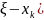 рублей следует распределить между предприятиями от первого до k-го так, чтобы была получена максимальная прибыль 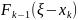. Тогда прибыль k предприятий будет равна 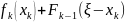. Нужно выбрать такое значение между 0 и 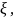чтобы эта сумма была максимальной, и мы переходим к рекуррентному соотношению:

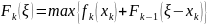
для k = 2, 3, 4, …, n. Если же k = 1, то .

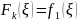Первым этапом решения задачи является составление таблицы 2. Значения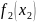 складываются со значениями 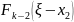и на каждой северо-западной диагонали отмечается максимальное значение:

Таблица 2.Второе предприятие

		0	100	200	300	400	500	600	700
		0	20	20	30	38	43	49	52
0	0	0	20*	20	30	38	43	49	52
100	13	13	33*	33	43	51	56	62
200	25	25	45*	45	55	63	68
300	37	37	57*	57	67	75
400	47	47	67*	67	77
500	55	55	75*	75
600	61	61	81*
700	67	67

Отмеченными значениями заполняется таблица 3 и указываются соответствующие значения :

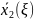Таблица 3.Второе предприятие

	0	100	200	300	400	500	600	700
	0	20	33	45	57	67	75	81
	0	0	100	200	300	400	500	600

Следующий этап – табулирование функции 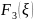, 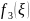(таблица 4) и составление таблицы 5:

Таблица 4.Третье предприятие

		0	100	200	300	400	500	600	700
		0	20	33	45	57	67	75	81
0	0	0	20*	33*	45*	57*	67*	75*	81
100	6	6	26	39	51	63	73	81*
200	13	13	33	46	58	70	80
300	20	20	40	53	65	77
400	27	27	47	60	72
500	33	33	53	66
600	38	38	58
700	41	41

Таблица 5.Третье предприятие

	0	100	200	300	400	500	600	700
	0	20	33	45	57	67	75	81
	0	0	0	0	0	0	0	100

В таблице 6 заполняется только диагональ для значения . Максимальное значение на этой диагонали 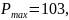следовательно четвертому предприятию должно быть выделено

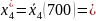200 тыс. руб.

Таблица 6. Четвертое предприятие

		0	100	200	300	400	500	600	700
		0	20	33	45	57	67	75	81
0	0								81
100	24							99
200	36						103*
300	42					99
400	46				91
500	48			81
600	48		68
700	49	49

На долю остальных предприятий остается 700 – 200 = 500 тыс. руб. Согласно таблице 5 третьему предприятию должно быть выделено:

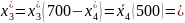0 тыс. руб.

Аналогично находим значение для второго предприятия:

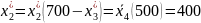тыс.руб.

На долю первого предприятия остается:

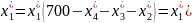тыс. руб.

Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:

.

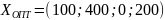Максимальный прирост прибыли составит (согласно таблице 1):

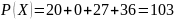тыс. руб.