
- •Задача линейного программирования, формулировка, математическая модель, алгоритм решения симплексным методом и в Excel. Постоптимизационный анализ решения задачи.
- •Двойственность в линейном программировании. Симметричная пара двойственных задач, правила составления, их экономическое содержание.
- •Двойственные оценки ресурсов и технологий. Математическая модель задачи определения двойственных оценок, их экономическое содержание.
- •Несимметричная пара двойственных задач, правила составления, её особенности.
- •Первая основная теорема двойственности и её экономическая интерпретация.
- •Вторая основная теорема двойственности и её экономическая интерпретация.
- •Третья основная теорема двойственности и её экономическая интерпретация.
- •Задача оптимального пополнения недостающих ресурсов на предприятии.
- •Применение метода динамического программирования при принятии решений об оптимальном распределений инвестиций.
- •Оптимизация плана распределения ресурсов между производственными подразделениями с помощью двойственных оценок при двухуровневой системе управления.
- •Задача целочисленного программирования. Решение методом Гомори, методом ветвей и границ, а также в Excel.
- •Многокритериальные задачи линейного программирования, решение методом последовательных уступок.
- •Векторы, действия над ними, линейная зависимость и независимость векторов, их линейная комбинация, базис.
- •Матрицы, их классификация, алгебра матриц.
- •Определители матриц их свойства и методы вычисления.
- •Метод динамического программирования, принцип оптимальности, параметр состояния, функция состояния, рекуррентные динамические соотношения.
- •Принятие решений в условиях полной неопределённости, матрицы последствий и рисков.
- •Принятие решений в условиях полной неопределённости, правило Вальда.
- •Принятие решений в условиях полной неопределённости, правило Сэвиджа.
- •Принятие решений в условиях полной неопределённости, правило Гурвица.
- •Принятие решений в условиях частичной неопределённости, матрицы последствий и рисков.
- •Принятие решений с помощью дерева решений.
- •Риск как среднее квадратическое отклонение. Бейесовский подход к принятию решений, методы снижения рисков.
- •Матричные игры, основные понятия и определения, решение игры в чистых стратегиях.
- •Теорема об активных стратегиях, решение матричных игр в смешанных стратегиях.
- •Упрощение и геометрическая интерпретация решения матричных игр.
- •Сведение решения игры к решению пары взаимно двойственных задач линейного программирования.
- •Некооперативные биматричные игры, основные понятия и определения. Анализ биматричной игры в некооперативном варианте.
- •Кооперативные биматричные игры, оптимальность по Парето, переговорное множество, арбитражные схемы Нэша, функция Нэша.
- •Экспертные методы принятия решений.
Двойственные оценки ресурсов и технологий. Математическая модель задачи определения двойственных оценок, их экономическое содержание.
№2
Несимметричная пара двойственных задач, правила составления, её особенности.
(1.1.)
при ограничениях по ресурсам:
 (1.2.)
(1.2.)
и при условии неотрицательности переменных:
(1.3.)
Правила составления аналогичны симметричной (см. №2), но с учетом следующих особенностей:
Ограничения двойственной задачи – неравенства. Если в условии функции двойственной задачи требуется найти min, то знак неравенства ≥0 если max , то ≤0.
Переменные произвольные по знаку, т.е. могут принимать как положительные, так и отрицательные значения.
Составление двойственной задачи:
Каждому равенству соответствуют неравенства:
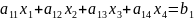
а)
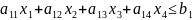
б)

Запишем каждое равенство на два неравенства:

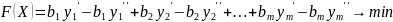 (1.1.)
(1.1.)



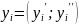

Первая основная теорема двойственности и её экономическая интерпретация.
Если одна из задач пары двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения линейных форм равны; если же форма одной из задач не ограничена, то и система условий другой задачи противоречива.
Симплекс-метод решения одной задачи приводит к решении другой, между переменными исходной и двойственной задач существует строгое и однозначное соответствие.
Экономические содержание:
В терминах оценок она м.б сформулирована следующим образом: если задача определения оптимального плана, оптимизирующего выпуск продукции, разрешима, то разрешима и задача определения min оценок ресурсов, причем цена продукта, полученного при реализации оптимального плана, совпадает с суммарной оценкой имеющихся ресурсов.
Вторая основная теорема двойственности и её экономическая интерпретация.
Для того чтобы допустимые решения
 ,
,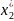 , … ,
, … ,
 )
и
)
и
 ,
, , … ,
, … ,
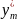 )
пары двойственных задач являлись
оптимальным решением этих задач,
необходимо и достаточно выполнение
условий:
)
пары двойственных задач являлись
оптимальным решением этих задач,
необходимо и достаточно выполнение
условий:

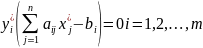
Т.о., если какое-либо неравенство системы ограничений одной из задач не обращается в точное равенство оптимальным решением этой задачи, то соответствующая компонента оптимального решения двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального решения одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимального решения должно обращаться в точное равенство. Другими словами:
Если
 для некоторого j,
то
для некоторого j,
то

Если
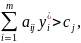 то
то

Если
 для некоторого i,
то
для некоторого i,
то
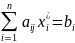
Если
 то
то

Экономическое содержание:
Следует обратиться к последним утверждениям (1-4).
3,4: если по оптимальному плану x*
производства расход i-го
ресурса
 строго меньше его запаса
т.е. если
,
то оценка
строго меньше его запаса
т.е. если
,
то оценка
 единицы этого ресурса равна нулю. Если
же оценка i-го ресурса
строго больше нуля, т.е.
,
то расход этого ресурса равен его запасу
единицы этого ресурса равна нулю. Если
же оценка i-го ресурса
строго больше нуля, т.е.
,
то расход этого ресурса равен его запасу

Т.о., оценки оптимального плана выступают как мера дефицитности ресурсов. Дефицитный ресурс – использованный полностью по оптимальному плану – имеет положительную оценку, а недефицитный ресурс – использованный не полностью – нулевую.
1,2: если оценки
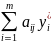 ресурсов, расходуемых по j-той
технологии в единицу времени строго
больше цены продукта, производимого по
той же технологии, т.е. если
ресурсов, расходуемых по j-той
технологии в единицу времени строго
больше цены продукта, производимого по
той же технологии, т.е. если
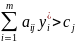 ,
то j-я технология не
применяется:
.
Если же по некоторому оптимальному
плану производства j-я
технология применяется, т.е. если
,
то оценка ресурсов, расходуемых по этой
технологии в единицу времени, равна
цене продукта, производимого по той же
технологии:
,
то j-я технология не
применяется:
.
Если же по некоторому оптимальному
плану производства j-я
технология применяется, т.е. если
,
то оценка ресурсов, расходуемых по этой
технологии в единицу времени, равна
цене продукта, производимого по той же
технологии:
Т.о., оценки оптимального плана выступают как инструмент определения эффективности отдельной технологии. Данный способ используется только в том случае, когда его реализационная оценка затраченных ресурсов и цена полученной продукции совпадают.
