Матричные игры, основные понятия и определения, решение игры в чистых стратегиях.
Математический аппарат, позволяющий описывать и систематизировать конфликт ситуаций целью разработки рекомендаций по выбору рационального образа действий каждой из сторон в ходе конфликтных ситуаций называется теорией игр.
В теории игр рассматриваются не сами ситуации, а их упрощенные схематизированные модели. Такие модели называются игрой. В отличие от реальных ситуаций, игра ведется по определенным правилам, стороны, участвующие в игре – игроки, результат столкновения сторон – выигрыш одной из сторон.
Для описания игры (построения модели) необходимо:
Определить число участников игры (обычно 2)
Указать возможные действия для каждой из сторон – стратегии. Выбор стратегии игроком вполне определяет течение игры, называется ходом.
Указать количественные оценки, всех возможных игровых ситуаций с т.зр. интересов игроков. Оценка может получить если каждый игровой ситуации приписывать некоторый выигрыш, получаемый данным игроком в рассматриваемой ситуации.
Игры с двумя противоположными интересами – самые простые и распространенные.
Если первый игрок выбрал i-ю
стратегию, а второй – j-ю,
то результатом такого выбора будет
платежная матрица П =
)
Строки этой матрицы соответствуют
стратегиям первого игрока, столбцы –
второго.
Игра происходит партиями. Партия игры состоит в том, что игроки одновременно называют свой выбор.
Цель каждого игрока – выиграть как можно большую сумму в результате большого числа партий
Стратегия называется чистой, если выбор игрока неизменен от партии к партии. У первого игрока есть m чистых стратегий, у второго – n.
При анализе игр противник считается сильным (разумным). Если первый игрок выбирает i-ю стратегию (строку матрицы П), то второй игрок выберет такую стратегию, чтобы обеспечить себе наибольший выигрыш, т.е. выберет такой столбец матрицы П, в котором платеж – минимален, т.е. перебирая все наши стратегии i = 1,2, … , m мы выберем такую, при которой второй игрок, действуя максимально разумно, заплатит нам наибольшую сумма.
Величина
– нижняя цена игры, а соответствующая
стратегия первого игрока – максиминной.
Аналогично (с т.зр. второго игрока)
определяется верхняя цена игры:
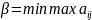и соответствующая стратегия – минимаксная
стратегия второго игрока.
Нижняя цена игры – минимальный гарантированный выигрыш первого игрока, а верхняя – величина, противоположная гарантированному выигрышу первого игрока.
Если
=
, то игра имеет седловую точку. Общее
значение
и
называется ценой игры и обозначается
буквой
.
При этом стратегии игроков, соответствующие
седловой точке, называются оптимальными
чистыми стратегиями, т.к. эти стратегии
наиболее выгодна сразу для обоих игроков,
обеспечивая первому игроку гарантированный
выигрыш не менее
,
а второму – гарантированный выигрыш
не менее –
Пример.
Найти цену игры и оптимальные стратегии.
Данная игра имеет седловую точку. Нижняя цена игры равна 0,3 (соответствует второй стратегии первого игрока). Верхняя цена игры – 0,3 (вторая стратегия второго игрока). Поэтому игроки, действия согласно своей стратегии, могут гарантировать себе:
Первый – выигрыш не менее 0,3. А второй
игрок – что первый выиграет не более
0,3. Т.о., оптимальная стратегия первого
и второго игроков – вторая, а цена игры
равна
