28. Принятие решений с помощью дерева решений.

Процесс принятия решений с помощью этого метода предполагает выполнение следующих этапов:

1. Формулировка задачи. Для того необходимо отбросить не относящиеся к проблеме факторы, а среди оставшихся выделить существенные и несущественные. Это позволит привести описание задачи применять к решении других, поддающихся анализу

2. Построение дерева решений – графическое изображение последовательности решений и состояния среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций, альтернатив и состояний среды.

3. Оценка вероятностей состоящей среды (указанные вероятности определяются на основании статистических данных или экспертным путем)

4. Установление выигрышей (проигрышей, как выигрышей со знаком «-») для каждой возможной комбинации альтернативы (действий) и состояний среды

5. Решение задачи.

Пример:

Руководство некоторой компании решает, создавать ли для выпуска новой продукции крупное производство, малое предприятие или продать патент другой фирме. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка (табл. 3.1).

На основе данной таблицы выигрышей (потерь) можно построить дерево решений (рис. 3.1).

Номер стратегии	Действие компании	Выигрыш, при состоянии эк. Среды
		благоприятном	Неблагоприятонм
1	Строительство крупного предприятия а1	200 000	-180 000
2	Строительство малого предприятия а2	100 000	-20 000
3	Продажа патента а3	10 000	-10 000

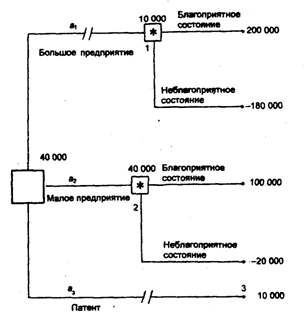
• Вероятность благоприятного и неблагоприятного состояний экономической среды равна 0,5.

Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ОДО.

Определим средний ожидаемый выигрыш (ОДО):

• для вершины 1 ОДО1 = 0,5*200 000 + 0,5(-180 000) = 10 000 дол.;

• для вершины 2 ОДО2 = 0,5*100 000 + 0,5(-20 000) = 40 000 дол.;

• для вершины 3 ОДО3 = 10 000 дол.

Вывод. Наиболее целесообразно выбрать стратегию а2, т.е. строить малое предприятие, а ветви (стратегии) а1 и а3 дерева решений можно отбросить. ОДО наилучшего решения равна 40 000 дол. Следует отметить, что наличие состояния с вероятностями 50 % неудачи и 50 % удачи на практике часто означает, что истинные вероятности игроку скорее всего неизвестны и он всего лишь принимает такую гипотезу (так называемое предположение «fifty - fifty» - пятьдесят на пятьдесят).

29. Риск как среднее квадратическое отклонение. Бейесовский подход к принятию решений, методы снижения рисков.

Пример 1.

Экспериментатор показал Вам два совершенно одинаковых на вид мешочка и сказал, что в одном из них 80% белых фасолин и 20% коричневых, а в другом – 20% белых и 80% коричневых. Затем он унес оба мешочка, вернулся с одним и предложил указать, каких фасолин в нем больше. Если угадаете правильно, получите 10 очков, не угадаете – ничего не получите. Стоит ли участвовать в этой игре?

Выигрыш V является случайной величиной с рядом распределения

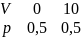
И средним выигрышем в расчете на одну игру MV = 0*0,5 + 10*0,5 = 5.

Пример 2.

Через некоторое время эксперементатор усложнил условия: он предложила вытащить одну фасолину, увидеть ее цвет и сказать, каких фасолин в мешочке больше. За это он попросил отдать 1 очко. Имеет ли смысл платить?

Вероятность угадывания равна вероятности вытащить из мешочка фасолину того цвета, который совпадает с большинством фасолин в этом мешочке. Но последняя вероятность равна 0,8. Вероятность выигрыша возросла, теперь ряд распределения выглядит так:

А средний выигрыш в расчете на одну игру MV = 0*0,2 + 10*0,8 = 8. Поэтому есть смысл платить за игру 1 очко.

В примерах – байесовский подход к принятию решений.