10. Основные параметры синусоидального тока

Переменным называют ток (напряжение, Э.Д.С.), изменяющийся во времени по величине и направлению. Синусоидальный ток может быть представлен посредством действительной функции времени – синусной или косинусной, например, 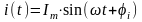,(3.1) где I_m – максимальная амплитуда тока (амплитудное значение);  – угловая частота, причем 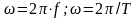; f – частота колебаний [Гц]; Т – период [C]; _i – начальная фаза, определяет значение тока в момент времени t=0, т.е. i(t=0) = I_m sin _i.

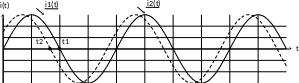
На рис. 3.1 приведен график двух колебаний с разными начальными фазами _{1 и} ₂, причем ₁ < ₂. Амплитуда гармоник проходит через нуль, когда t +  = n, (n = 0,1,2...), т.е. в моменты 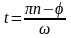. Так как ₁< ₂, то t₂ имеет место раньше t₁.

Рис. 3.1. Графики мгновенных значений синусоидального тока i₁(t) = I_m∙sin ωt и I₂(t) = I_m∙sin(ωt+30º) Начальная фаза часто задается в градусах. Поэтому при определении мгновенного значения тока аргумент синуса (слагаемые t и ) нужно привести к одной единице измерения (радиан или градус). Иногда гармоническое колебание представляется в косинусной форме. Легко видеть, что для перехода к такой форме в (3.1) достаточно изменить лишь начальную фазу, т.е.

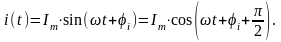
Промышленная частота переменного тока в России и всех странах Европы равна 50 Гц, в США и Японии - 60 Гц, в авиации - 400 Гц. Снижение промышленной частоты ниже 50 Гц ухудшает качество освещения. Увеличение частоты ухудшает условия передачи электроэнергии на большие расстояния.

Выражение для синусоидального напряжения аналогично (3.1), т.е. u(t) = U_m  sin (t + _u).(3.2)

Кроме уже названных параметров в практике электротехники часто пользуются понятиями среднего и действующего значений тока и напряжения. Рассмотрим их.

Под средним значением синусоидального тока понимают его среднее значение за половину периода: 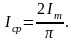(3.3) Видим, что среднее значение синусоидального тока составляет 2/  0,64 от амплитудного значения. Аналогично определяется среднее значение синусоидального напряжения: . Действующим называют среднее квадратичное значение синусоидального тока (напряжения) за период 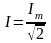.(3.4)

Видим, что действующее значение синусоидального тока составляет 0,707 от амплитудного значения. Аналогично определяется действующее значение синусоидального напряжения: .

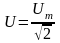Если говорят о значениях переменного тока или напряжения, то, как правило, подразумевают их действующие значения. Например, напряжение в однофазной сети переменного тока 220 В - действующее. При этом амплитудное значение U_m  310 В.

11. Символический метод анализа цепей синусоидального тока.

Все параметры цепи представляются в комплексной форме.

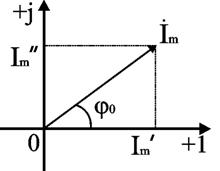– комплексное мгновенное значение;– комплексное действующее значение силы тока; – комплексное действующее значение напряжения.Законы Ома и Кирхгофа в комплексной форме.Достоинство комплексного метода: при его применении в анализе цепей переменного тока можно применять все известные методы анализа постоянного тока.

Закон Ома.Под законом Ома в комплексной форме понимают: Í = Ú / Z

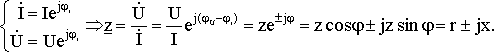
Комплексное сопротивление участка цепи представляет собой комплексное число, вещественная часть которого соответствует величине активного сопротивления, а коэффициент при мнимой части – реактивному сопротивлению.По виду записи комплексного сопротивления можно судить о характере участка цепи:R + j X — активно-индуктивное сопротивление; R – j X — активно-емкостное.

Первый закон Кирхгофа в комплексной форме

Алгебраическая сумма комплексных действующих значений токов в узле равна нулю.

Второй закон Кирхгофа в комплексной форме

В замкнутом контуре электрической цепи алгебраическая сумма комплексных действующих значений ЭДС равна алгебраической сумме комплексных падений напряжений в нём.

. При использовании символического метода можно пользоваться понятиями мощностей. Но в комплексной форме можно записать только полную мощность: где Ï — комплексно-сопряженный ток.

S cos φ ± j S sin φ = P ± j Q.Полная мощность в комплексной форме представляет собой комплексное число, вещественная часть которого соответствует активной мощности рассматриваемого участка, а коэффициент при мнимой части – реактивной мощности участка. Значение знака перед мнимой частью: “+” означает, что напряжение опережает ток, нагрузка – активно-индуктивная; “–” означает, что нагрузка - активно-емкостная.