- •1. Неопределённый интеграл и его свойства.
- •Свойства неопределенного интеграла
- •2. Таблица основных неопределённых интегралов
- •3. Замена переменной в интеграле. Примеры.
- •4. Интегрирование по частям. Примеры
- •5. Определённый интеграл и его геометрический смысл.
- •6. Основные свойства определенного интеграла
- •7. Интеграл с переменным верхним пределом и его свойства. Формула Ньютона-Лейбница.
- •8. Вычисление площадей плоских фигур
- •9. Вычисление длины дуги
- •10. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл первого рода)
- •11. Признаки сходимости несобственных интегралов первого рода.
- •12. Несобственный интеграл второго рода. Примеры
- •14. Множества в Rn. Основные понятия и определнения.
- •16. Понятие функции нескольких переменных. Примеры.
- •17. Предел функции нескольких переменных в точке и его свойства.
- •19. Частные производные фнп
- •24. Полный дифференциал функции нескольких переменных. Инвариантность формы первого дифференциала.
- •Инвариантность формы первого дифференциала
- •Свойства инвариантности
- •25. Применение дифференциала в приближенных вычислениях
- •26. Производные и дифференциалы высших порядков.
- •27. Формула Тейлора для функции нескольких переменных.
- •28. Экстремум функции двух переменных
19. Частные производные фнп
Рассмотрим линию
![]() пересечения поверхности
с плоскостью
пересечения поверхности
с плоскостью
![]() ,
параллельной плоскости
,
параллельной плоскости
![]() .
Так как в этой плоскости
сохраняет постоянное значение, то
вдоль кривой
будет меняться только в зависимости от
изменения
.
Дадим независимой переменной
приращение
.
Так как в этой плоскости
сохраняет постоянное значение, то
вдоль кривой
будет меняться только в зависимости от
изменения
.
Дадим независимой переменной
приращение
![]() ,
тогда
получит приращение, которое называется
частным
приращением
по
и обозначают через
,
тогда
получит приращение, которое называется
частным
приращением
по
и обозначают через
![]() ,
так что
,
так что
![]() .
.
Наконец, придав
аргументу
приращение
,
а аргументу
приращение
![]() ,
получим для
новое приращение
,
получим для
новое приращение
![]() ,
которое называется полным
приращением
функции
и определяется формулой
,
которое называется полным
приращением
функции
и определяется формулой
![]() .
.
На рисунке
изображено отрезком
![]() .
.
Надо отметить,
что, вообще говоря, полное приращение
не равно сумме частных приращений, т.е.
![]() .
.
Определение1
Частной
производной по
от функции
называется предел отношения частного
приращения
по
к
приращению
при стремлении
к нулю. Обозначается:
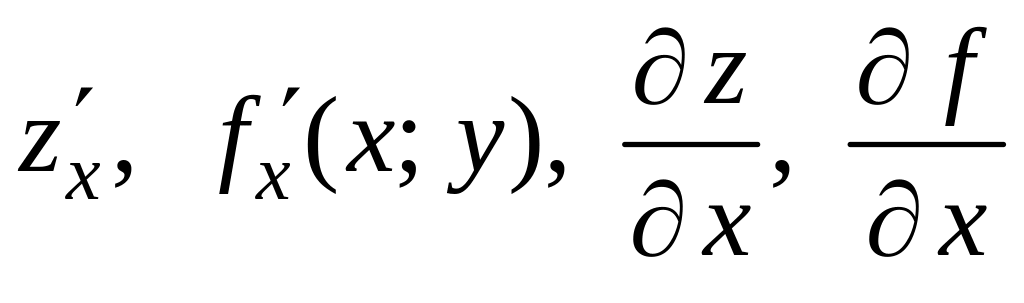 .
Тогда
.
Тогда
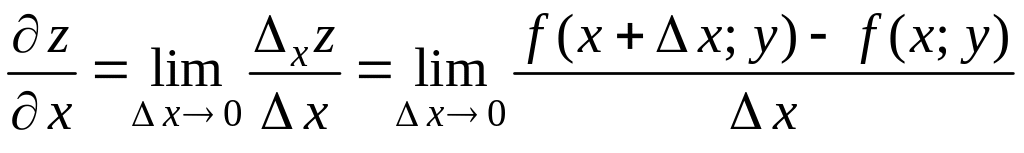 .
(1)
.
(1)
Определение 2
Частной
производной по
от функции
называется предел отношения частного
приращения
![]() по
к
приращению
при стремлении
к нулю. Обозначается:
по
к
приращению
при стремлении
к нулю. Обозначается:
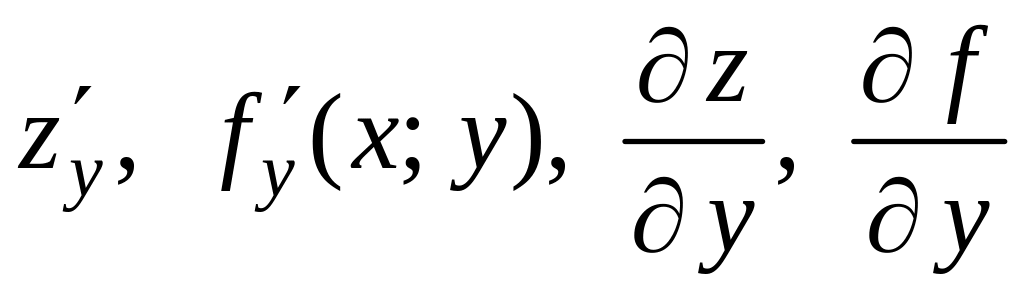 .
Тогда
.
Тогда
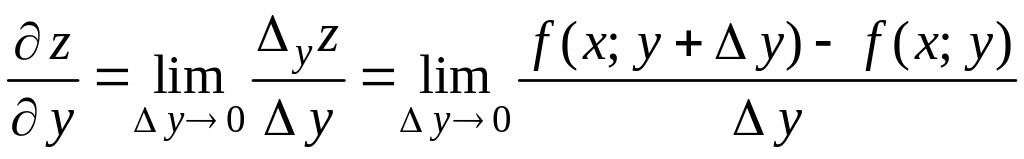 .
(2)
.
(2)
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно или считаются постоянной величиной).
Пример 2.1.
Для данной функции требуется найти
частные производные
![]() и
и
![]() .
Найти значения частных производных в
точке
.
Найти значения частных производных в
точке
![]() :
:
![]() .
.
Решение. Находим частные производные в общем виде:
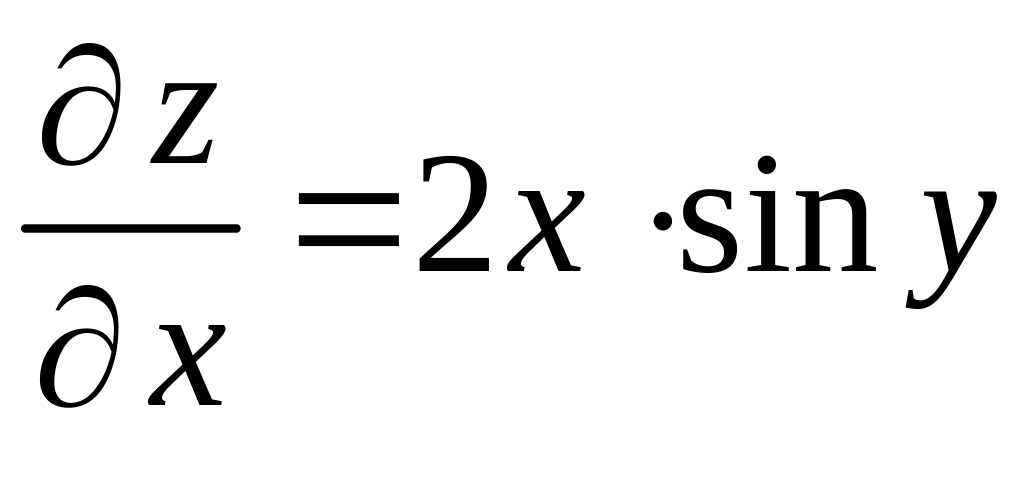 ,
,
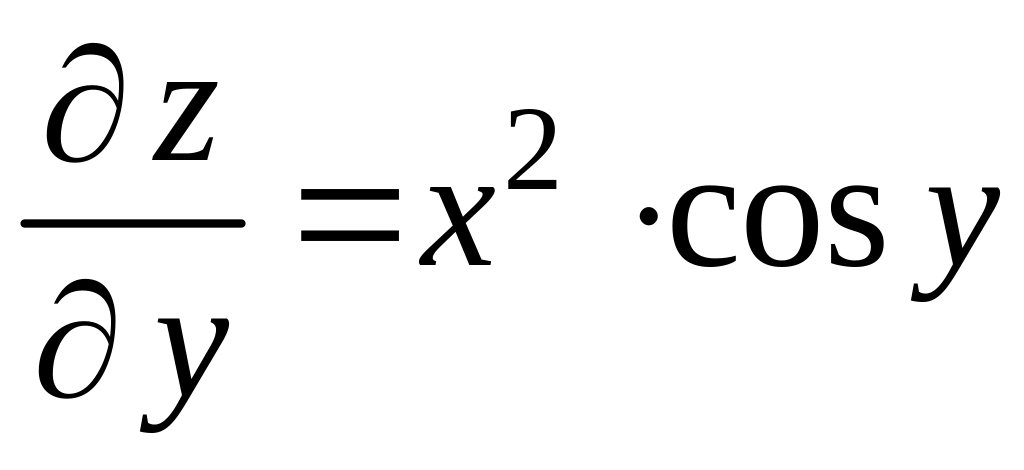 .
.
Находим значения частных производных в точке :
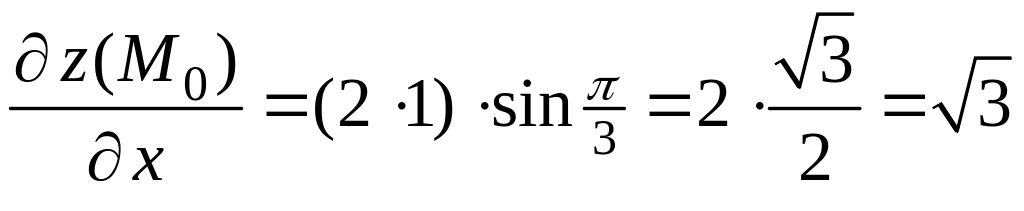 ,
,
 .
.
24. Полный дифференциал функции нескольких переменных. Инвариантность формы первого дифференциала.
Пусть функция z = f(x, y) диф-ма в т. P0(x0, y0)
Опр. 1
Полным
дифференциалом
ф-и z
= f(x, y)
в т. Р0,
соответствующ. приращениям ![]() независимых переменных, называется
главная часть приращения этой функции,
линейная относительно
.
независимых переменных, называется
главная часть приращения этой функции,
линейная относительно
.
![]()
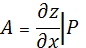 0,
0,
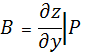 0
0
![]() ,
то
,
то
 P0∙
P0∙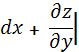 P0∙
P0∙![]()
 ∙
∙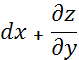 ∙
∙![]() (1)
(1)
U=f(x,y,z)
dU=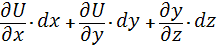 ;
;
Z=f(x1...xn)
dz=![]() ∙d
∙d![]()
В силу равенства
![]()
![]()
![]()
![]() (2)
(2)
Пр. 1
Найти дифференциал z=![]()
![]()
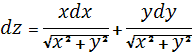
Пр. 2
Вычислить ![]() (1,02)2,99
(1,02)2,99
f(x,y)
= ![]()
x0=1, y0=3
![]()
f
`x(x,y)=y∙![]()
![]()
(1,02)2,99
13+3∙12∙0,02+13∙![]() ∙(-0,01)=1+0,06=1,06
∙(-0,01)=1+0,06=1,06
Инвариантность формы первого дифференциала
Пусть ![]()
![]() :
: 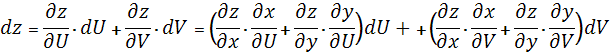 =
=
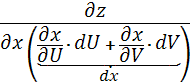 +
+
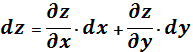
Свойства инвариантности
1. ![]()
2. ![]()
3.
25. Применение дифференциала в приближенных вычислениях
Рассмотрим вопрос об использовании дифференциала в приближенных вычислениях.
Известно, что∆y=y’∆x+α∆x и dy=y’∆x
поэтому можно записать∆y=dy+ α∆x
Это позволяет сделать вывод о том, что ∆y≈dy
т.е. приближенное значение приращения функции совпадает с ее дифференциалом.
Функция может быть довольно сложное выражение и ее приращение не всегда просто
найти, но при достаточно малых значениях |Δx|приращение функции можно заменить ее
дифференциалом, исключая точки, где у' = 0.
Отсюда находим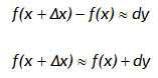 Это
одна из основных формул для приближенных
вычислений
Это
одна из основных формул для приближенных
вычислений
Пример 1.
Пользуясь понятием дифференциала функции, вычислить приближенно изменение
функции y = x3 – 7x2 + 80 при изменении аргумента х от 5 до 5,01
Решение.
Находим Δу≈ dy = y' Δx = (3x2 – 14x) Δx.
При х = 5, Δx = 5,01 – 5 = 0,01 получим
Δу|x=5, Δx = 0,01 = (3. 52 – 14. 5) . 0,01 = (3. 25 - 14 . 5) . 0.01 = 0,05
Вычисление погрешности приближенного приращения функции.
Абсолютная и относительная погрешности.
Рассмотрим функцию y = f(x). Предположим, что величина х получена непосредственным
измерением или в результате приближенного вычисления. Тогда при нахождении
величины х допускается некоторая погрешность Δх.
Пусть х – приближенное значение аргумента (измеряемой величины),
Δх – абсолютная погрешность величины х,
(х + Δх) – истинное значение измеряемой величины (Δх может быть как положительным, так и отрицательным числом).
Тогда х определяет приближенное значение функции f(х), а (х +Δх) – ее истинное значение f(х + Δх), из чего следует, что точное приращение функции Δy = f( х + Δх) - f(х).
При близких к нулю значениях Δх величину Δy можно приближенно заменить дифференциалом dy:
![]()
Тогда абсолютная погрешность вычисляется по формуле
Δ = |Δy - dy|,
а относительная
по формуле:
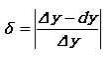
Пример 2.
Найти приближенно приращение функции у = 3х2 + 2 при х =2 и Δx = 0,001. Определить абсолютную и относительную погрешности вычисления.
Решение.
Так как приращение аргумента - величина малая, то приращение функции можно
заменить ее дифференциалом:
Δу ≈dу|x=2, Δx = 0,001 = 6xdx|x=2, Δx = 0,001 = 6. 2. 0,001 = 0,012
Найдем ошибку, полученную при замене приращения функции ее дифференциалом. Для
этого вычислим точное значение приращения функции:
Δу = f(x + Δx) – f(x) = 3(x + Δx)2 + 2 – (3x2 + 2) = 3x2 + 6xΔx+ +3(Δx)2 + 2 – 3x2 – 2 = 6xΔx +3(Δx)2;
Δу|x=2, Δx = 0,001 = 6. 2. 0,001 + 3. 0,000001 = 0,012003.
Сравнивая точное значение Δу с приближенным, видим, что абсолютная погрешность есть Δ = |Δy – dy| = 0,000003.
Относительная
погрешность составляет