12. Несобственный интеграл второго рода. Примеры

Определение 1. Пусть функция непрерывна на промежутке и имеет бесконечный разрыв при . Если существует конечный предел 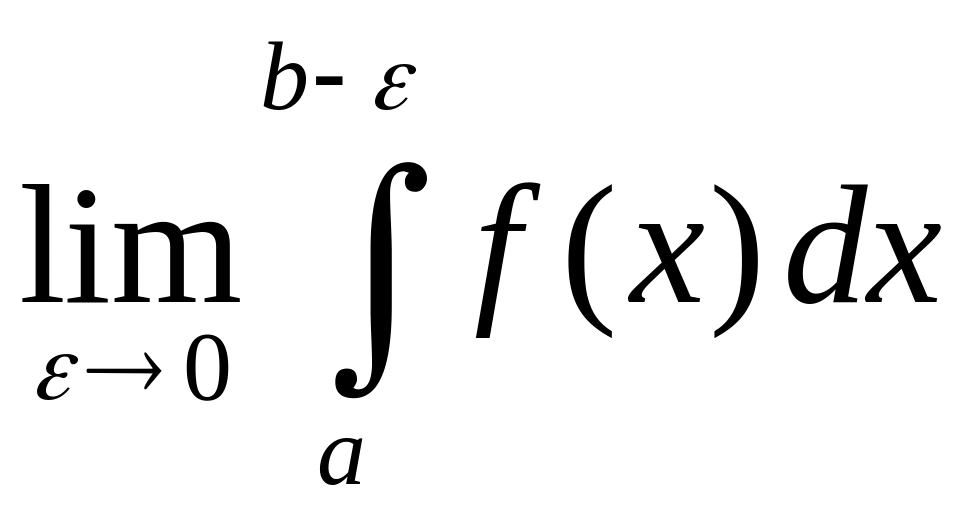, где , то его называют сходящимся несобственным интегралом второго рода и обозначают , т.е.

. (1)

Если же указанный предел не существует или он бесконечен, то говорят, что интеграл расходится.

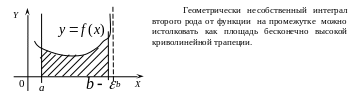
Аналогично, если функция терпит бесконечный разрыв в точке , то полагают

.

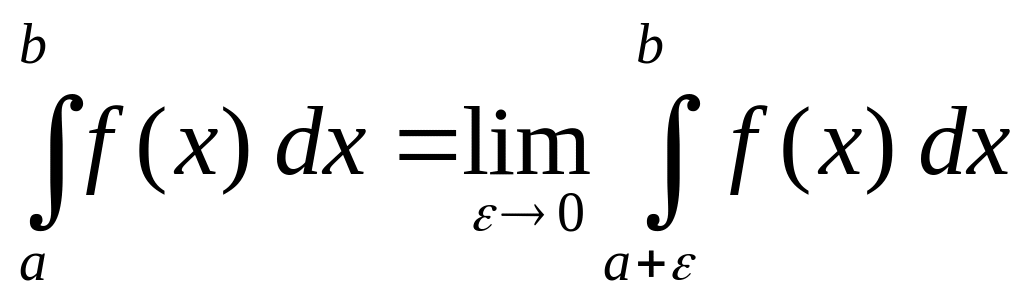Если функция терпит разрыв во внутренней точке отрезка , то несобственный интеграл второго рода определяется формулой

.

В этом случае интеграл слева называют сходящимся, если оба предела, стоящих справа существуют.

Пример1. Вычислить несобственный интеграл или установить его расходимость:

.

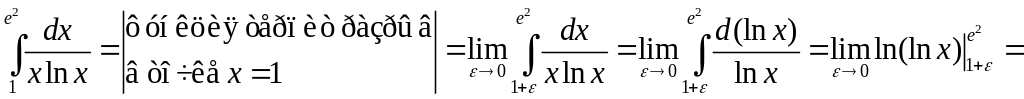
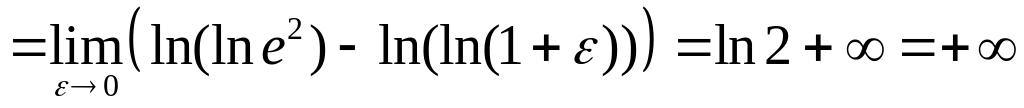Следовательно, данный интеграл расходится.

Пример 2. Вычислить несобственный интеграл или установить его расходимость:

.

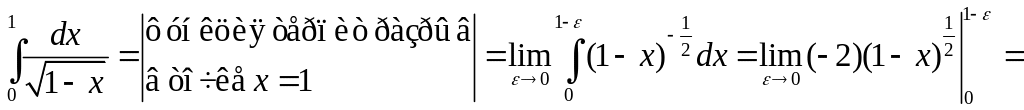
Следовательно, данный интеграл сходится.

14. Множества в Rn. Основные понятия и определнения.

Рассмотрим множество . За расстояние между точками

х и у примем величину , что соответствует обычной евклидовой норме.

δ − окрестностью т. называется множество точек х, удовлетворяющих условию: , где δ − заданное положительное число. При n = 2 или 3 это будет соответственно круг или шар (без границы), радиуса δ.

Кроме круговой (шаровой) окрестности будем использовать и прямоугольную окрестность : координатный прямоугольник со сторонами 2δ и центром в т.x^o.

Точка называется внутренней т. множества D, если

Точка называется граничной т. множества D, если

Множество всех граничных точек называется границей множества D.

Множество, не содержащее ни одной граничной точки, называется открытым.

Множество, содержащее все свои граничные точки, называется замкнутым .

Множество называется связным, если две его любые точки можно соединить непрерывной кривой, целиком принадлежащей этому множеству.

Областью называется связное открытое множество.

Множество называется односвязным, если любая непрерывная замкнутая кривая, принадлежащая множеству, может быть стянута в одну точку. В противном случае множество называется многосвязным.

Множество называется ограниченным, если оно целиком лежит внутри некоторой δ−окрестности и неограниченным в противном случае.

Любая ограниченная область, содержащая т. х^о называется окрестностью этой точки.

16. Понятие функции нескольких переменных. Примеры.

Определение 1. Если каждой паре из некоторой области их изменения , поставлено в соответствие определенное значение величины , то говорят, что есть функция двух независимых переменных и . Записывается

.

При этом и называются независимыми переменными (аргументами), а  зависимой переменной (функцией).

Определение 2. Множество пар значений и , при которых определена функция , называется областью определения функции, обозначается .

Если каждую пару значений и можно изобразить точкой на плоскости , то область определения функции изобразиться в виде некоторой совокупности точек этой плоскости. В частности, область определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями.

Определение 3. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой.

Пример 1.1. Найти область определения функции

.

Решение. Областью определения данной функции является множество точек плоскости , которые удовлетворяют решению системе неравенств

.



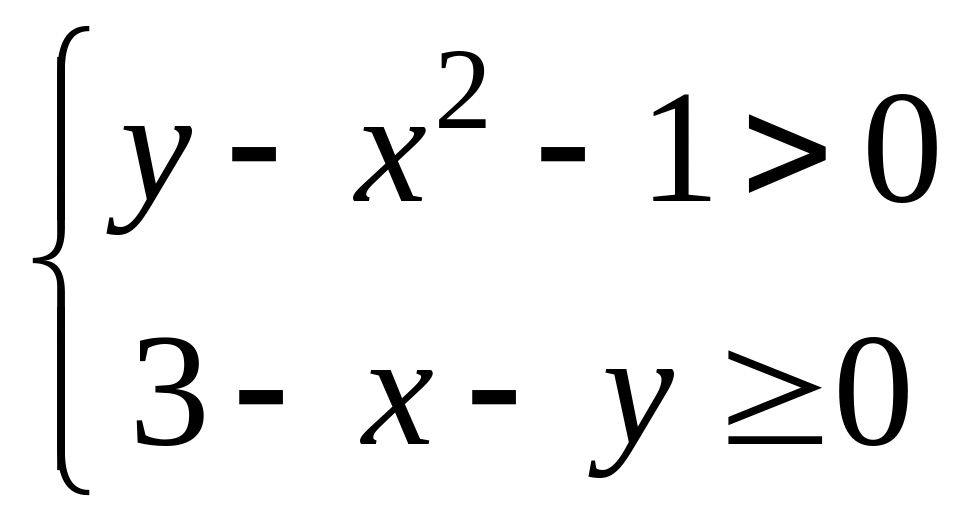Определение функции двух переменных легко обобщить на случай трех или более переменных.

Определение 4. Если каждой рассматриваемой совокупности значений переменных соответствует определенной значение переменной , то называют функцией независимых переменных и записывают

.

Так же как и для функции двух переменных, можно говорить об области определения функции трех, четырех и более переменных. Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графически.

Рассмотрим функцию , определенную в области на плоскости , и систему прямоугольных декартовых координат . В каждой точке

Определение 5. Геометрическое место точек , координаты которых удовлетворяют уравнению , называется графиком функции двух переменных.

Из курса аналитической геометрии известно, что уравнение в пространстве определяет некоторую поверхность. Таким образом, графиком функции двух