
- •1. Неопределённый интеграл и его свойства.
- •Свойства неопределенного интеграла
- •2. Таблица основных неопределённых интегралов
- •3. Замена переменной в интеграле. Примеры.
- •4. Интегрирование по частям. Примеры
- •5. Определённый интеграл и его геометрический смысл.
- •6. Основные свойства определенного интеграла
- •7. Интеграл с переменным верхним пределом и его свойства. Формула Ньютона-Лейбница.
- •8. Вычисление площадей плоских фигур
- •9. Вычисление длины дуги
- •10. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл первого рода)
- •11. Признаки сходимости несобственных интегралов первого рода.
- •12. Несобственный интеграл второго рода. Примеры
- •14. Множества в Rn. Основные понятия и определнения.
- •16. Понятие функции нескольких переменных. Примеры.
- •17. Предел функции нескольких переменных в точке и его свойства.
- •19. Частные производные фнп
- •24. Полный дифференциал функции нескольких переменных. Инвариантность формы первого дифференциала.
- •Инвариантность формы первого дифференциала
- •Свойства инвариантности
- •25. Применение дифференциала в приближенных вычислениях
- •26. Производные и дифференциалы высших порядков.
- •27. Формула Тейлора для функции нескольких переменных.
- •28. Экстремум функции двух переменных
8. Вычисление площадей плоских фигур
1)
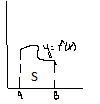 f(x)
>=0., S
=
f(x)
>=0., S
= 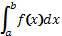 ,
,
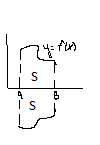
f(x)<=0
-f(x)>=0,
S
= 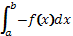 =
=
2)
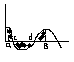 S
=
S
= 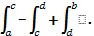
3)
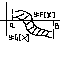 S=
S=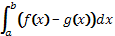
Предположим, что линия, ограничивающая криволинейную трапецию, является графиком функции, заданной параметрически:
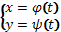 ,
X€[a,b]
соотв. t€[α,β]
,
X€[a,b]
соотв. t€[α,β]
S=
=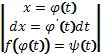 =
= 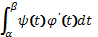
S(эллипса) = πab
Пусть дана функция
r=f(![]() ,
где r
и
,
где r
и ![]() - полярные координаты. r=f(
- криволинейный сектор.
- полярные координаты. r=f(
- криволинейный сектор.

![]()
![]() ,
,
S(кр.сект.)=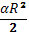
![]()
![]() f(
f(![]() )
=
)
= ![]()
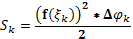
S
S=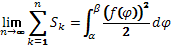
S(сект) =
9. Вычисление длины дуги
Длина гладкой кривой между двумя точками с абсциссами и находится по формуле (в декартовой системе координат:
 .
(1.1)
.
(1.1)
Когда кривая
![]() задана параметрическими уравнениями
и
задана параметрическими уравнениями
и
![]() ,
где
,
,
где
,
![]()
непрерывно дифференцируемые функции,
длина дуги вычисляется по формуле:
непрерывно дифференцируемые функции,
длина дуги вычисляется по формуле:
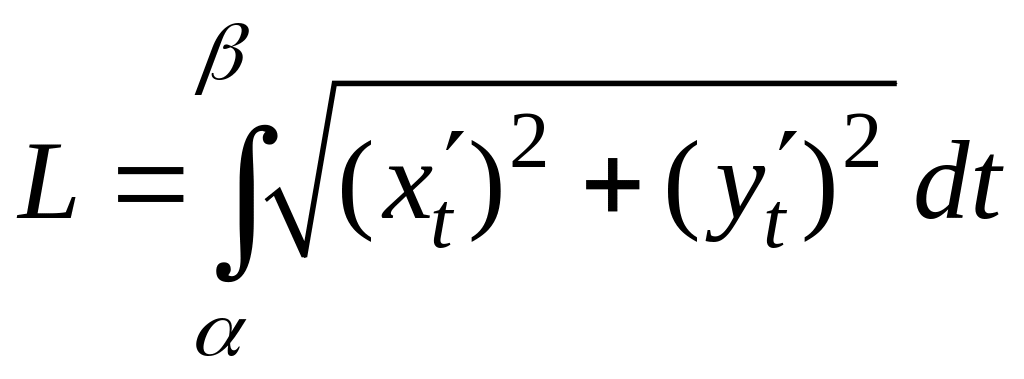 .
(1.2)
.
(1.2)
Здесь
![]() и
и
![]()
значения параметра
значения параметра
![]() ,
соответствующие концам дуги
,
соответствующие концам дуги
![]() и
и
![]() .
.
Если гладкая кривая
задана в полярных координатах уравнением
![]() ,
то длина дуги
,
то длина дуги
![]() вычисляется по формуле
вычисляется по формуле
 ,
(1.3)
,
(1.3)
где
![]() и
и
![]() соответствуют концам
соответствуют концам
![]() и
и
![]() .
.
10. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл первого рода)
Определение 5.1.
Пусть функция
непрерывна на промежутке
![]() .
Если существует конечный предел
.
Если существует конечный предел
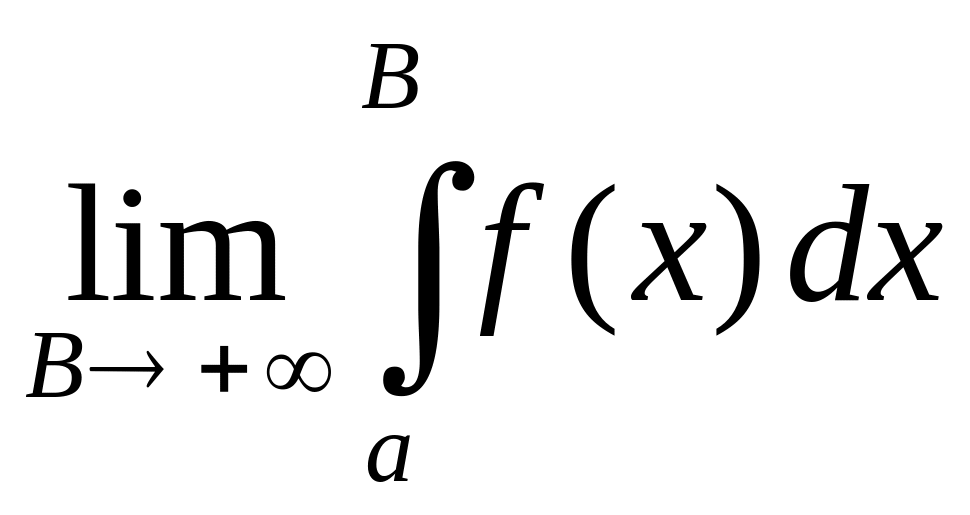 ,
то его называют сходящимся
несобственным интегралом первого рода
и обозначают
,
то его называют сходящимся
несобственным интегралом первого рода
и обозначают
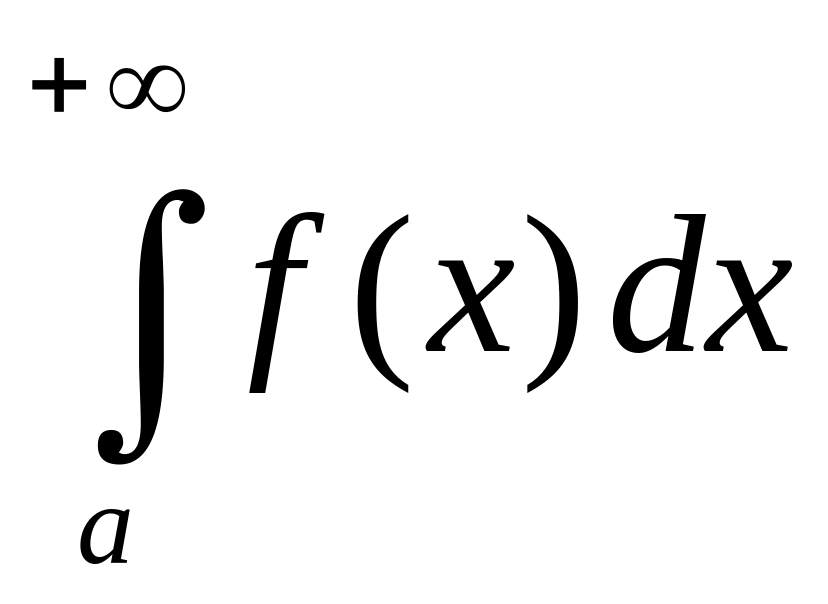 ,
т.е.
,
т.е.
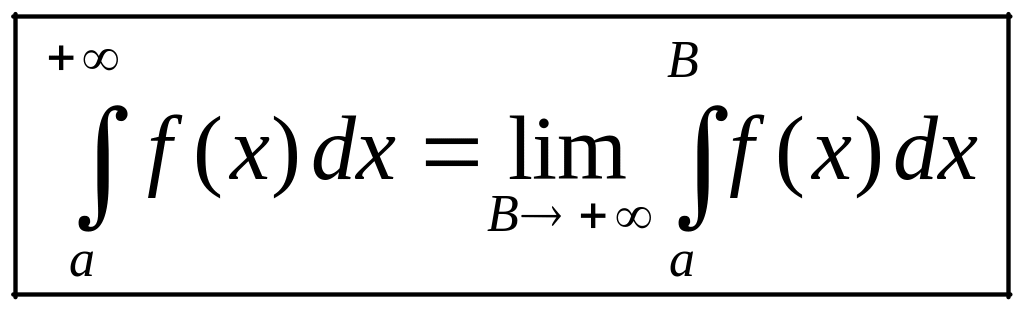 .
(1)
.
(1)
Если же указанный предел не существует или он бесконечен, то говорят, что интеграл расходится.
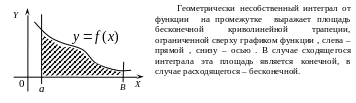
Аналогично
определяется несобственный интеграл
на промежутке
![]() :
:
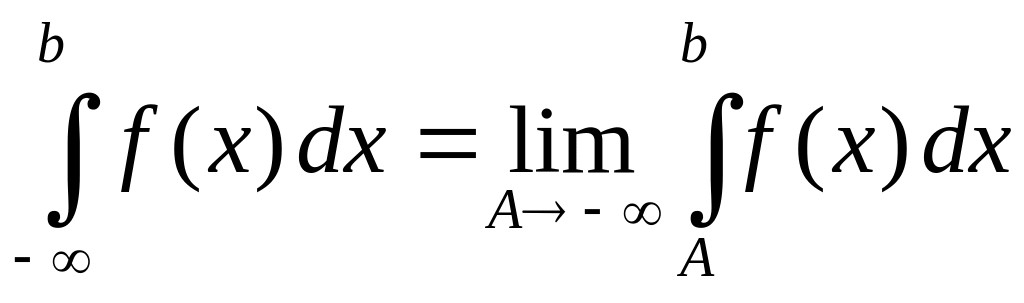 .
.
Несобственные интегралы с двумя бесконечными пределами определяются формулой
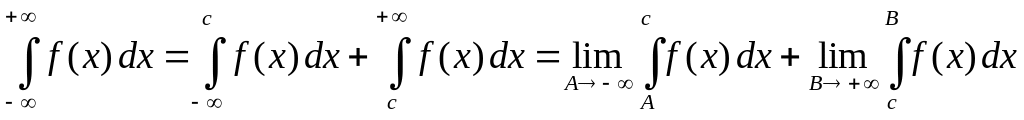 ,
,
где произвольное число.
Пример 1.
Дан интеграл
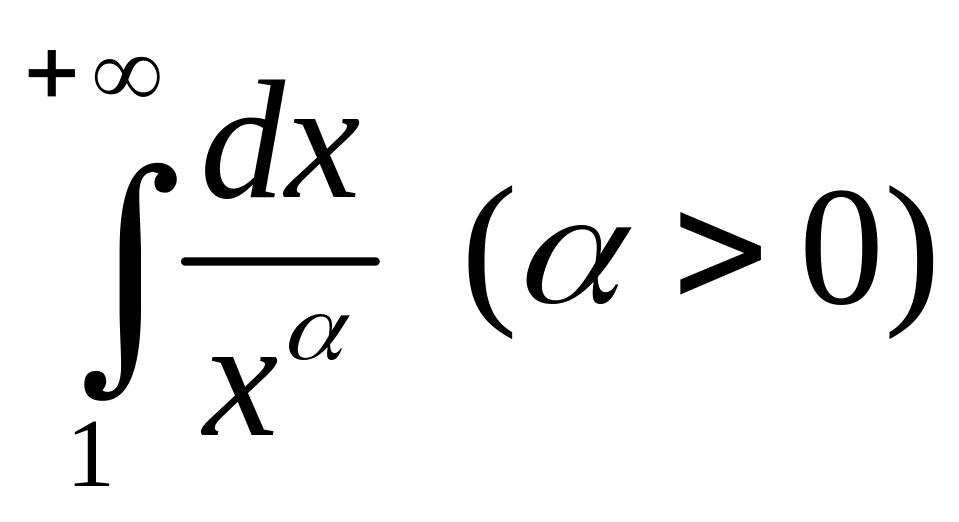 .
Установить, при каких значениях
этот интеграл сходится, а при каких –
расходится.
.
Установить, при каких значениях
этот интеграл сходится, а при каких –
расходится.
Решение.
Предположим, что
![]() .
Тогда
.
Тогда
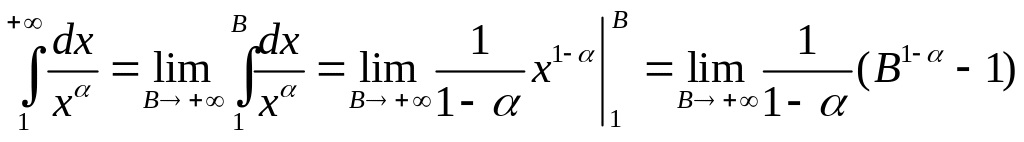 .
.
Следовательно,
если
![]() ,
то
,
то
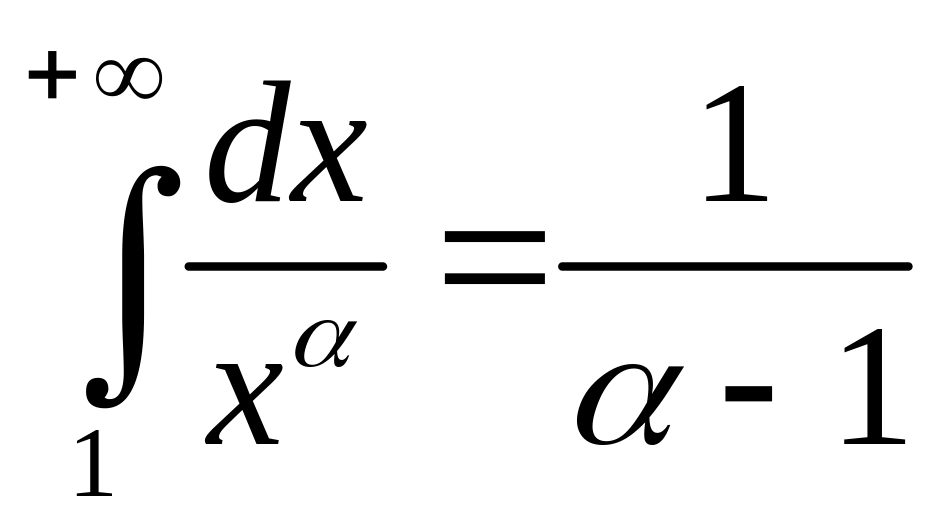 ,
т.е. данный интеграл сходится.
,
т.е. данный интеграл сходится.
Если
![]() ,
то
,
то
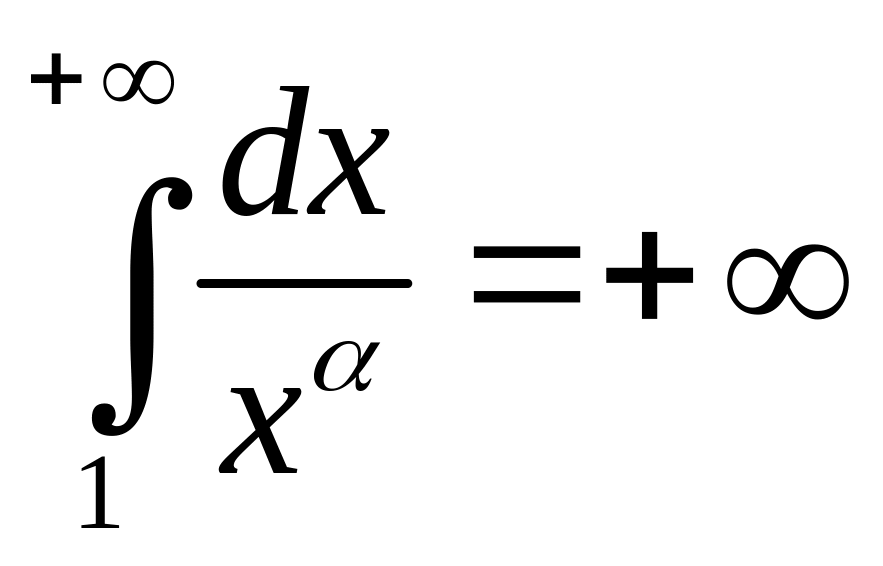 ,
т.е. интеграл расходится.
,
т.е. интеграл расходится.
При
![]() имеем
имеем
 ,
т.е. данный интеграл расходится.
,
т.е. данный интеграл расходится.
11. Признаки сходимости несобственных интегралов первого рода.
Установить условную сходимость несобственного интеграла по бесконечному промежутку при отсутствии абсолютной сходимости позволяют два следующих признака:
признак сходимости Абеля:
1. пусть функции
f(x) и g(x) определены в промежутке
![]() ,
причём f(x) интегрируема в этом промежутке,
т.е. интеграл
,
причём f(x) интегрируема в этом промежутке,
т.е. интеграл
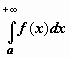 сходится (условно или абсолютно);
сходится (условно или абсолютно);
2. g(x) монотонна и
ограничена:
![]() .
.
Тогда интеграл
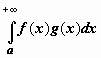 сходится.
сходится.
признак сходимости Дирихле:
пусть функция f(x) интегрируема в любом конечном промежутке [a, b], и интеграл по этому промежутку ограничен (как функция верхнего предела b):
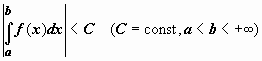 ;
;
2. g(x) монотонно
стремится к нулю при
![]() :
:
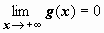 .
.
Тогда интеграл сходится.
Применим, например,
признак Дирихле к
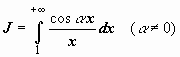 .
Здесь f(x) = cos x, g(x) = 1/x, условия признака
выполнены, поэтому интеграл сходится
условно.
.
Здесь f(x) = cos x, g(x) = 1/x, условия признака
выполнены, поэтому интеграл сходится
условно.
Теорема (признак
сравнения).
Если на промежутке
непрерывные функции
и
![]() удовлетворяют условию
удовлетворяют условию
![]() ,
то
,
то
1) если сходится
интеграл
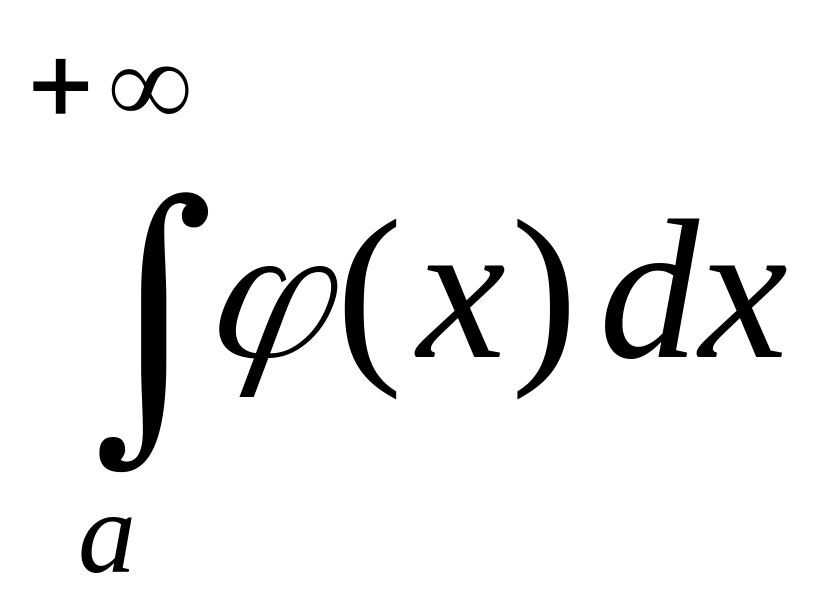 ,
то сходится и интеграл
;
,
то сходится и интеграл
;
2) если расходится интеграл , то расходится и интеграл .
Пример.
Доказать, что интеграл
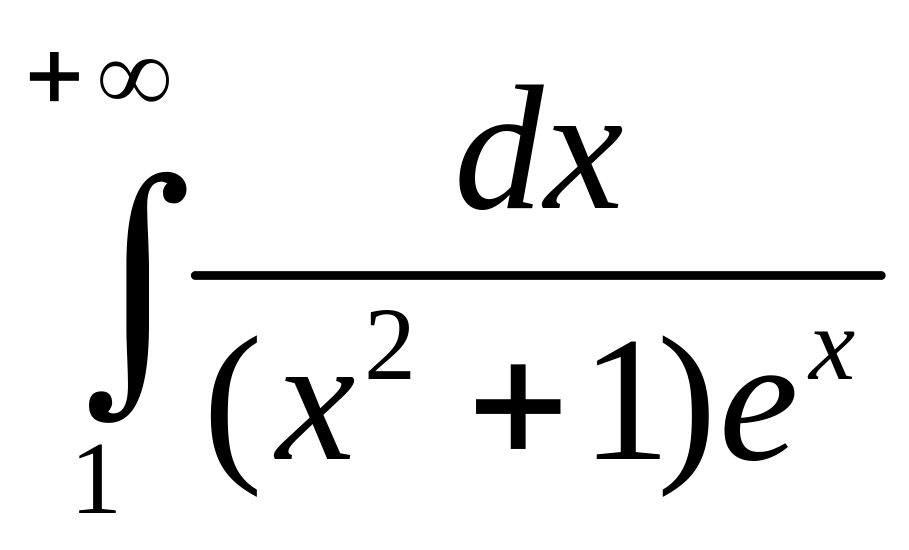 сходится.
сходится.
Доказательство.
Так как
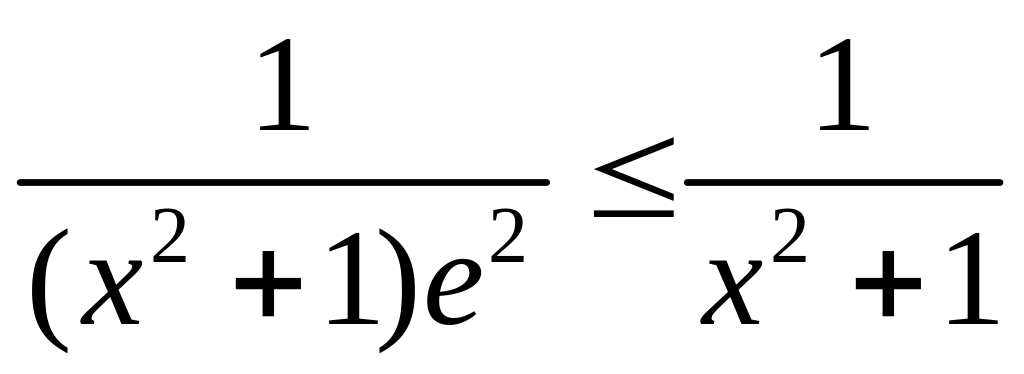 при
при
![]() и интеграл
и интеграл
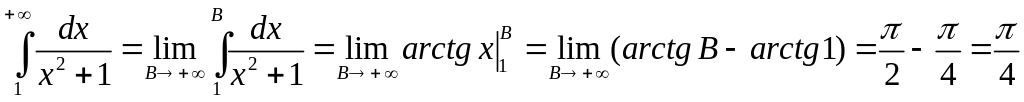
сходится, то исходный интеграл также сходится.
