6. Основные свойства определенного интеграла

Свойство 1. Если и функция интегрируема на отрезке , то

.

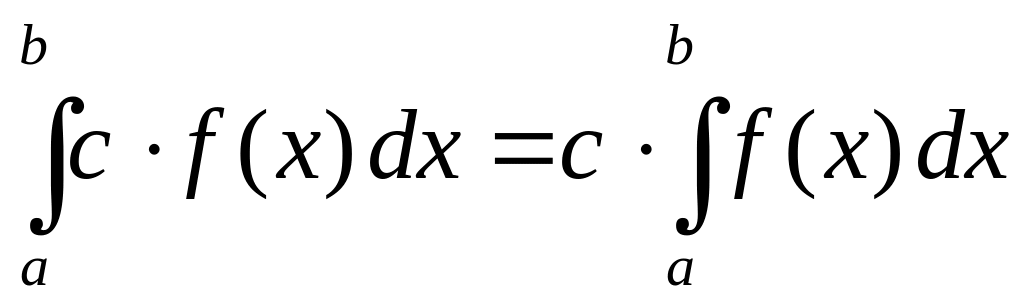Свойство 2. Если функции и интегрируемы на отрезке , тогда интегрируема на их сумма. Интеграл суммы равен сумме интегралов.

.

Доказательство.

.

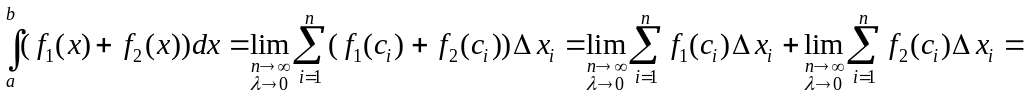
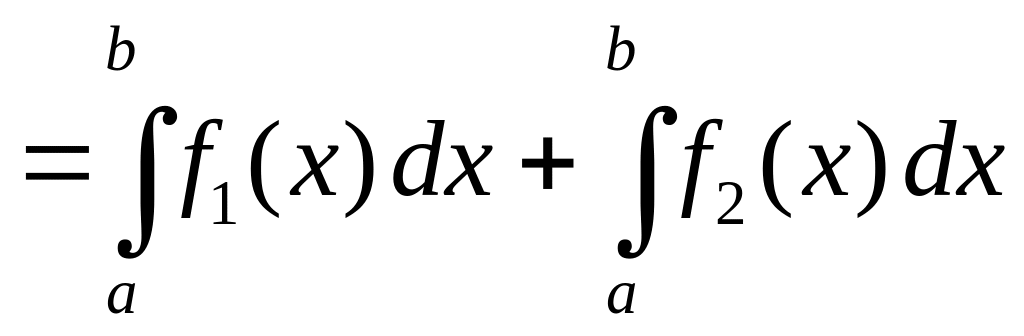Свойство 3. .

Свойство 4 (свойство аддитивности). Если функция интегрируема на отрезке и , то интеграл по всему отрезку равен сумме интегралов по частям этого отрезка:

,

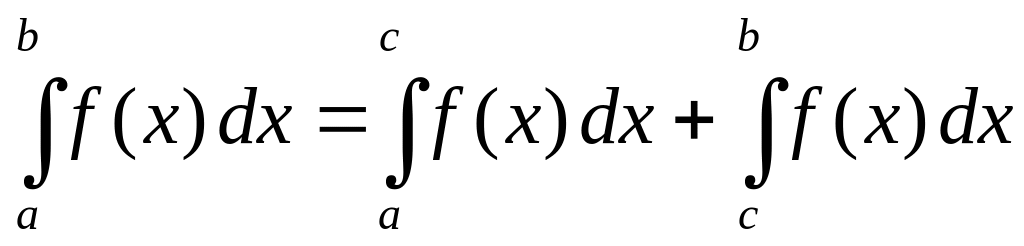Свойство 5 (теорема о среднем). Если функция непрерывна на отрезке , то существует точка , такая, что справедливо равенство

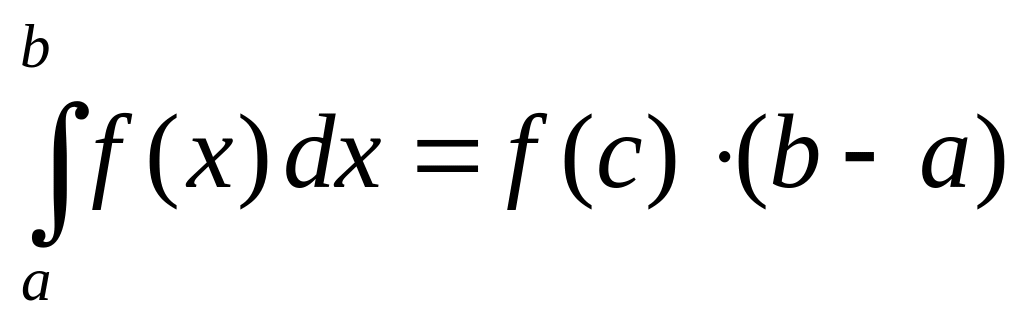. (1)

Доказательство. Пусть . Согласно теореме об ограниченности непрерывной на отрезке функции имеем , где  наименьшее значение функции, а  наибольшее значение функции на отрезке .

Очевидно, что если взять произвольное разбиение отрезка , то справедливы неравенства

.

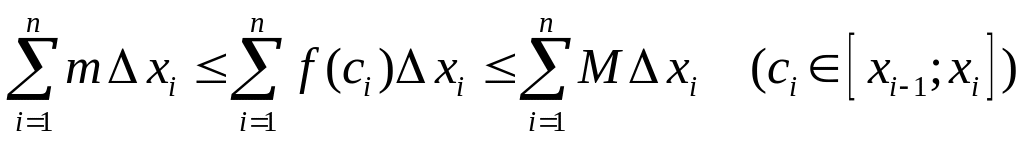Перейдем к пределу в неравенствах, если . Тогда получаем .

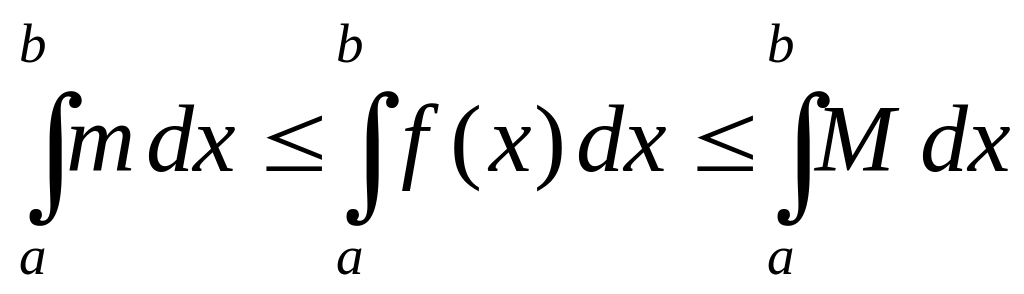Далее ,

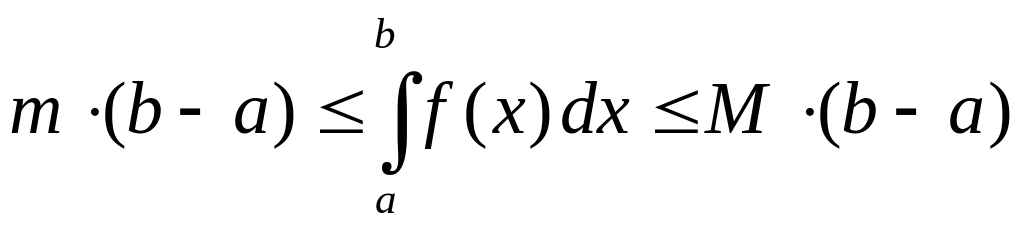Откуда .

Непрерывная на отрезке функция принимает на нем все свои промежуточные значения между и . Поэтому найдется точка , такая, что 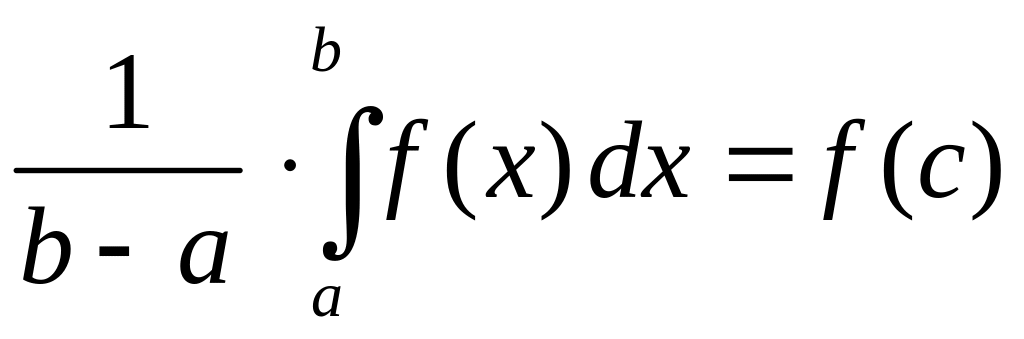,откуда следует формула (1).

Если , то .



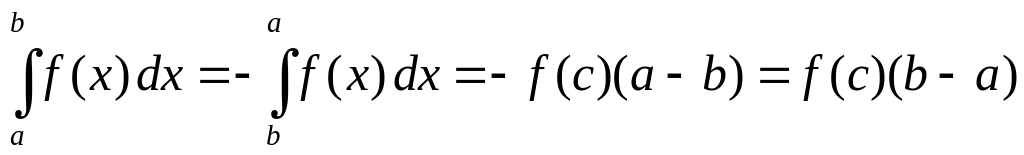Свойство 5 (теорема о среднем) при имеет простой геометрический смысл: значение определенного интеграла, при некотором , равно площади прямоугольника с высотой и основанием . Число

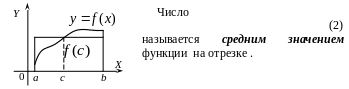
7. Интеграл с переменным верхним пределом и его свойства. Формула Ньютона-Лейбница.

Пусть функция непрерывна на отрезке . Тогда она интегрируема и на любом отрезке , где , т.е. для любого имеет смысл интеграл 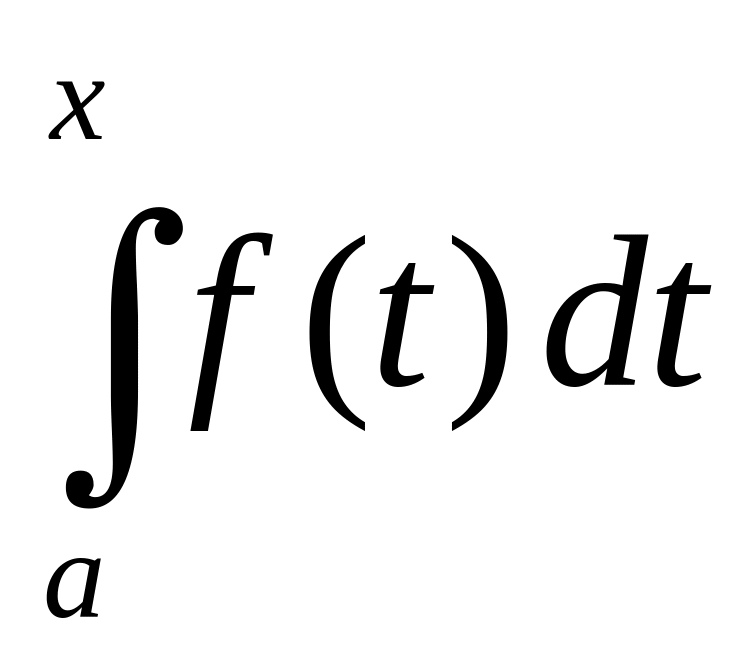. Рассмотрим функцию

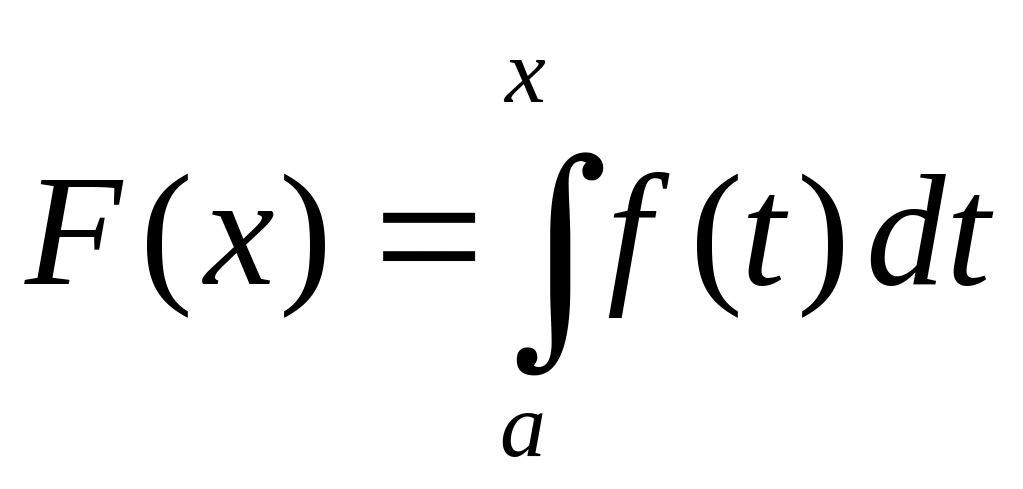, (1)

которая определена на отрезке и называется интегралом с переменным верхним пределом.

Выделим 2 основных св-ва этой функции:

1) непрерывна на [a,b]

2) Если функция непрерывна и диф-ма на отрезке , то производная функции существует в каждой точке , причем

.

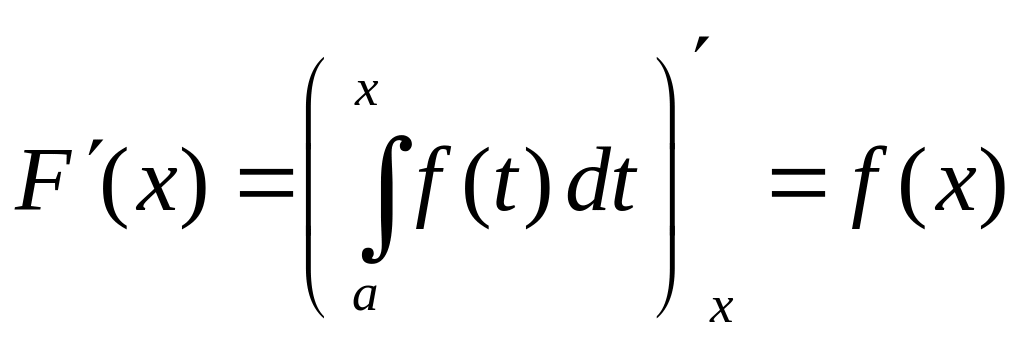Надо отметить, что любая функция , непрерывная на отрезке , имеет первообразную, определяемую формулой (1)

Теорема 1. Если функция непрерывна и диф-ма на отрезке , то производная функции существует в каждой точке , причем

.

Надо отметить, что любая функция , непрерывная на отрезке , имеет первообразную, определяемую формулой (1).

Теорема (формула Ньютона-Лейбница): если функция непрерывна на отрезке и  какая-нибудь первообразная для на этом отрезке, то справедлива формула НьютонаЛейбница

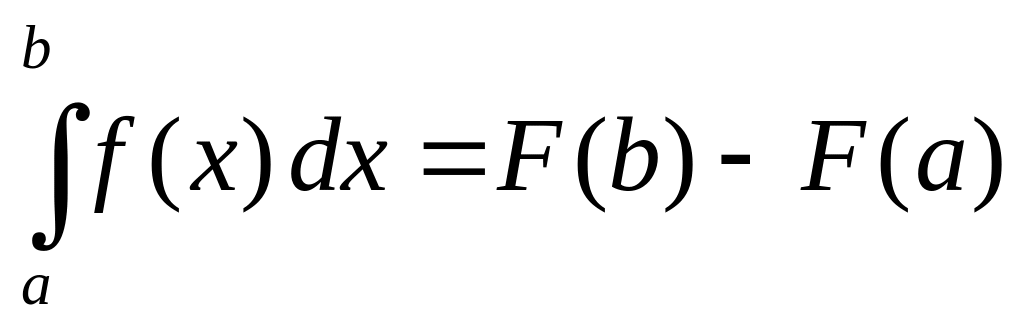. (2)

Доказательство. Рассмотрим интеграл с переменным верхним пределом

,

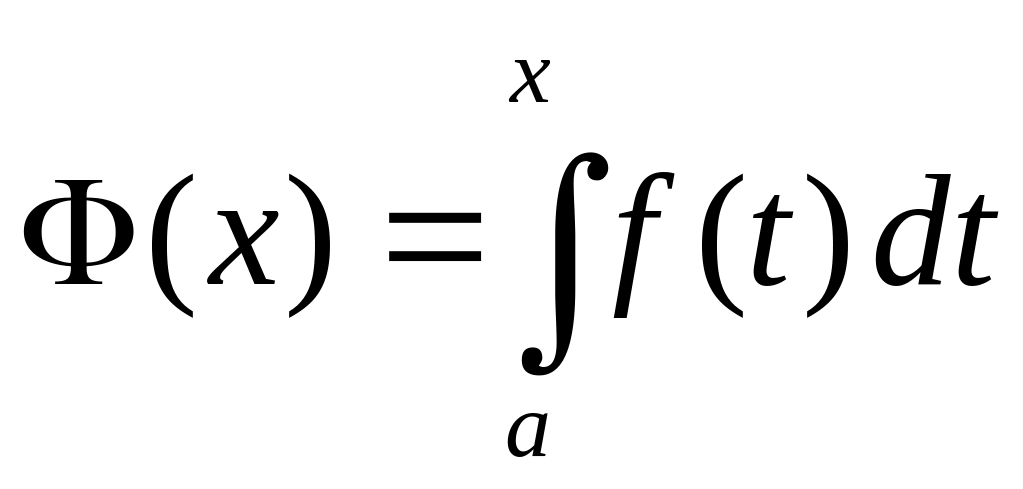где , на котором непрерывна. Согласно теореме 1, .

Пусть  первообразная функции , т.е. . Тогда по теореме 1.1 заключаем, что

.

При получаем

.

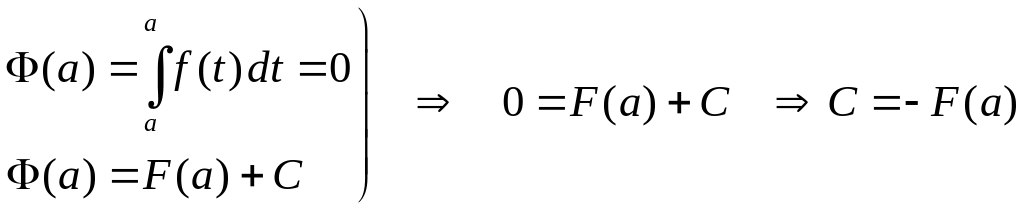Далее

,

или

.

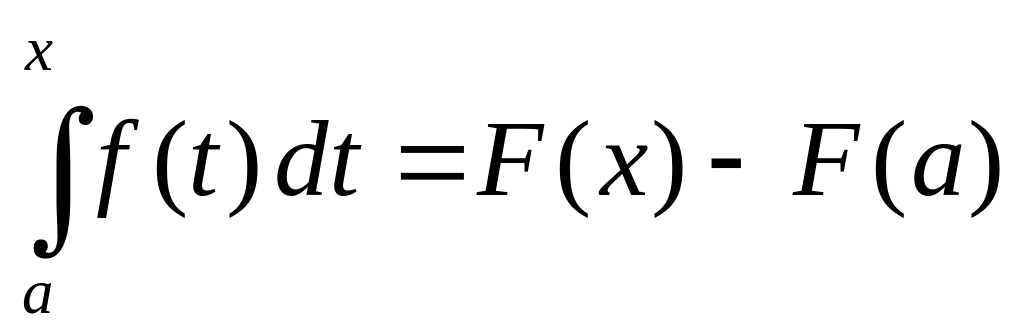При получаем

.

По свойству о независимости переменных получаем

.

Формулу НьютонаЛейбница (2) можно записать в виде

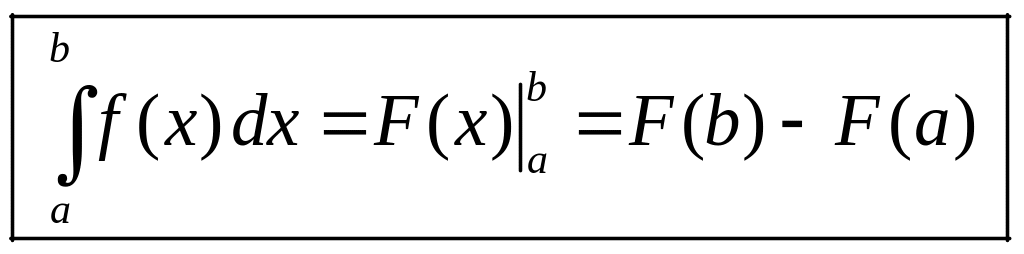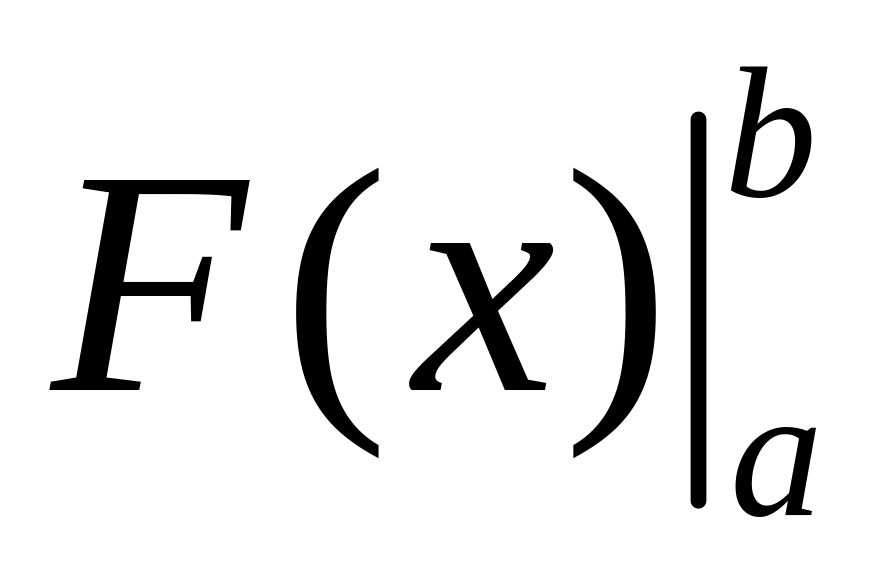
,где  называется двойной подстановкой от до для функции .