
- •1. Неопределённый интеграл и его свойства.
- •Свойства неопределенного интеграла
- •2. Таблица основных неопределённых интегралов
- •3. Замена переменной в интеграле. Примеры.
- •4. Интегрирование по частям. Примеры
- •5. Определённый интеграл и его геометрический смысл.
- •6. Основные свойства определенного интеграла
- •7. Интеграл с переменным верхним пределом и его свойства. Формула Ньютона-Лейбница.
- •8. Вычисление площадей плоских фигур
- •9. Вычисление длины дуги
- •10. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл первого рода)
- •11. Признаки сходимости несобственных интегралов первого рода.
- •12. Несобственный интеграл второго рода. Примеры
- •14. Множества в Rn. Основные понятия и определнения.
- •16. Понятие функции нескольких переменных. Примеры.
- •17. Предел функции нескольких переменных в точке и его свойства.
- •19. Частные производные фнп
- •24. Полный дифференциал функции нескольких переменных. Инвариантность формы первого дифференциала.
- •Инвариантность формы первого дифференциала
- •Свойства инвариантности
- •25. Применение дифференциала в приближенных вычислениях
- •26. Производные и дифференциалы высших порядков.
- •27. Формула Тейлора для функции нескольких переменных.
- •28. Экстремум функции двух переменных
1. Неопределённый интеграл и его свойства.
Определение 1.2.
Совокупность всех первообразных функций
![]() ,
где
,
где
![]() для функции
для функции
![]() называется неопределенным
интегралом от
функции
и обозначается
называется неопределенным
интегралом от
функции
и обозначается
![]() ,
т.е.
,
т.е.
![]() .
(1.1)
.
(1.1)
Здесь
называется подынтегральной
функцией,
![]()
подынтегральным
выражением,
подынтегральным
выражением,
![]()
переменной
интегрирования,
символ
переменной
интегрирования,
символ
![]()
знак
неопределенного интеграла.
знак
неопределенного интеграла.
Заметим следующее: если производная от элементарной функции всегда является элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций.
График первообразной
от функции
называется интегральной
кривой
функции
![]() .
Очевидно, мы получим любую другую
интегральную кривую, если пере-
.
Очевидно, мы получим любую другую
интегральную кривую, если пере-
параллельном движении одной из них по вертикали.
Свойства неопределенного интеграла
Свойство 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции.
![]() ,
,
![]()
Доказательство. Действительно,
![]() ,
,
и
![]() .
.
Благодаря свойству 1 правильность интегрирования проверяется дифференцированием.
Свойство 2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
![]() .
.
Доказательство. Действительно,
![]()
Свойство 3. Постоянный множитель можно выносить за знак интеграла:
![]() .
.
Свойство 4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций:
![]() .
.
Свойство 5
(инвариантность формулы интегрирования).
Если
![]() ,
то и
,
то и
![]() ,
где
,
где
![]()
произвольная функция, имеющая непрерывную
производную.
произвольная функция, имеющая непрерывную
производную.
2. Таблица основных неопределённых интегралов
Определение 1. Совокупность всех первообразных функций , где для функции называется неопределенным интегралом от функции и обозначается , т.е.
. (1)
Здесь называется подынтегральной функцией, подынтегральным выражением, переменной интегрирования, символ знак неопределенного интеграла.
Таблица основных интегралов
1.
![]() ;
2.
;
2.
![]() ;
;
3.
 ;
4.
;
4.
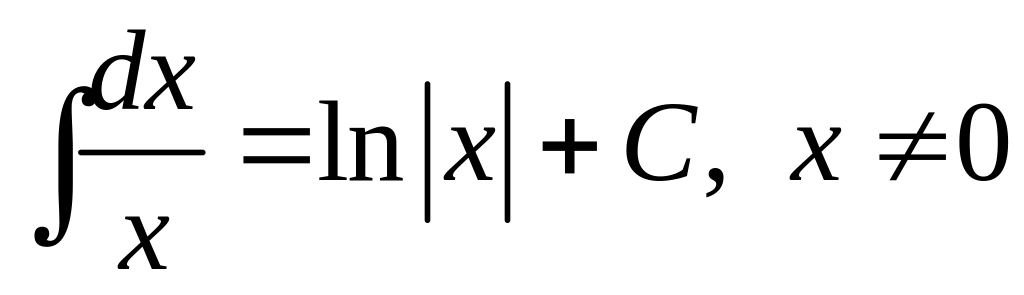 ;
;
5
![]() ;
11.
;
11.
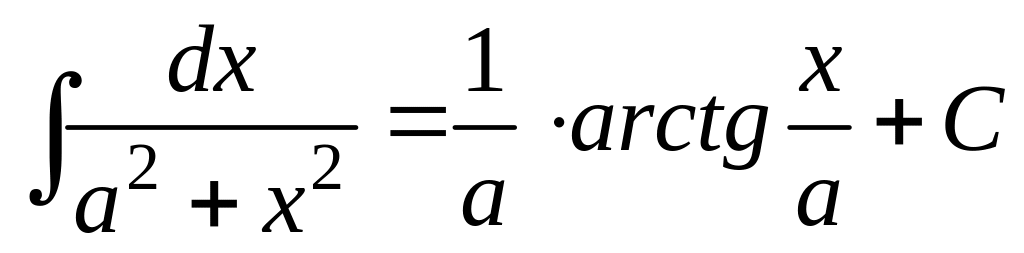 ;
;
6.
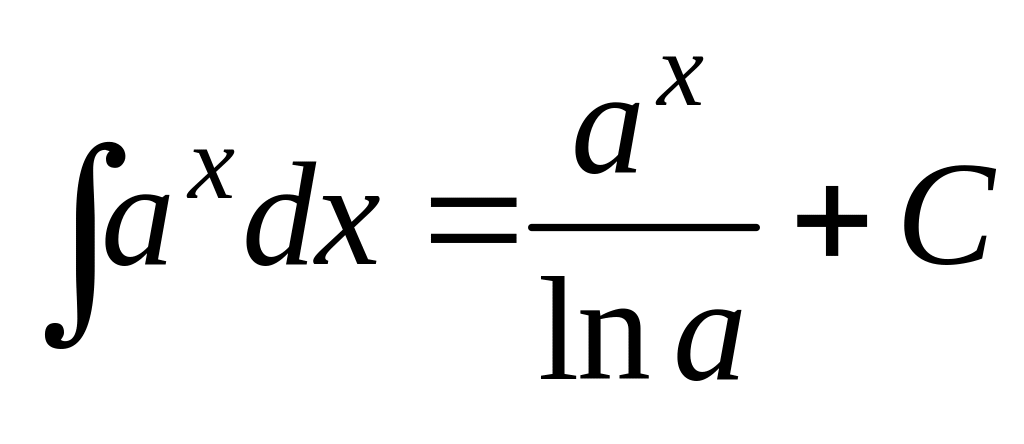 ;
12.
;
12.
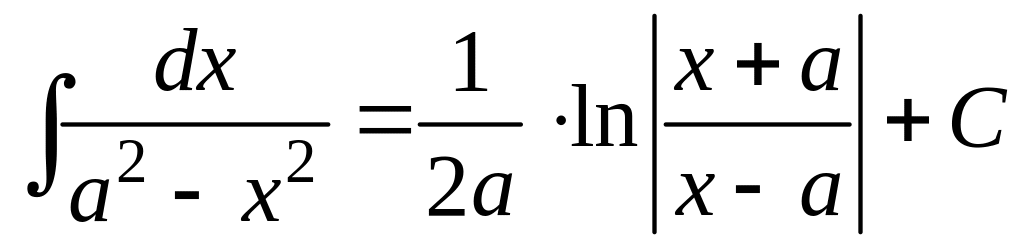 ;
;
7.
![]() ;
13.
;
13.
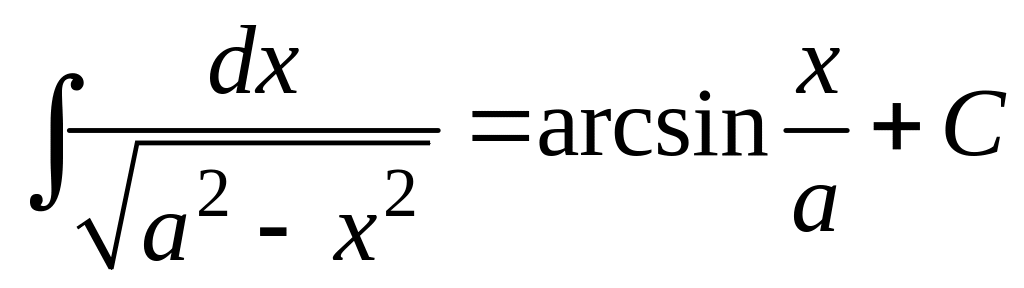 ;
;
8.
![]() ;
;
14.
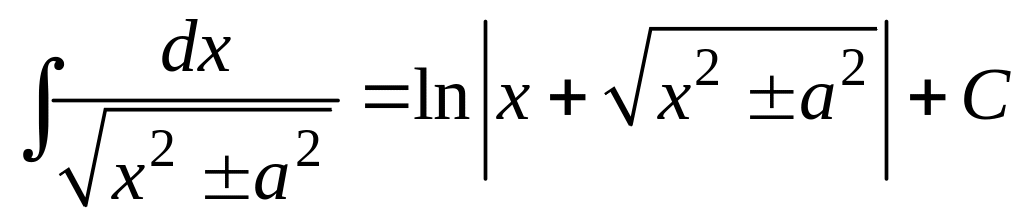 .
.
9.
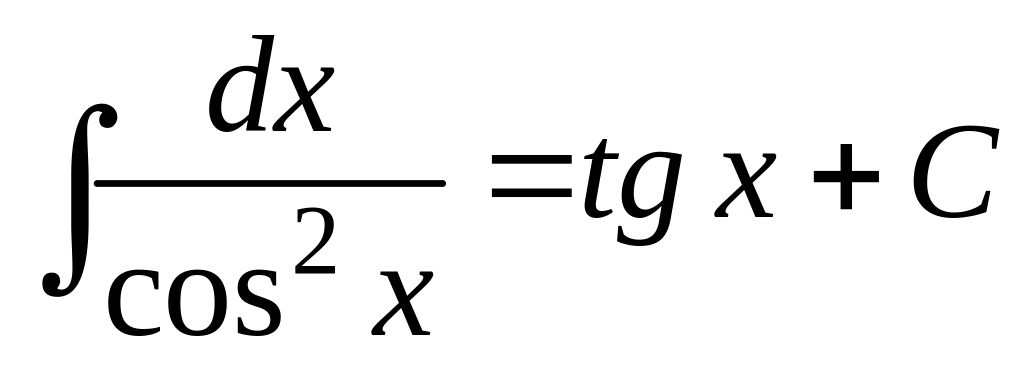 ;
;
10.
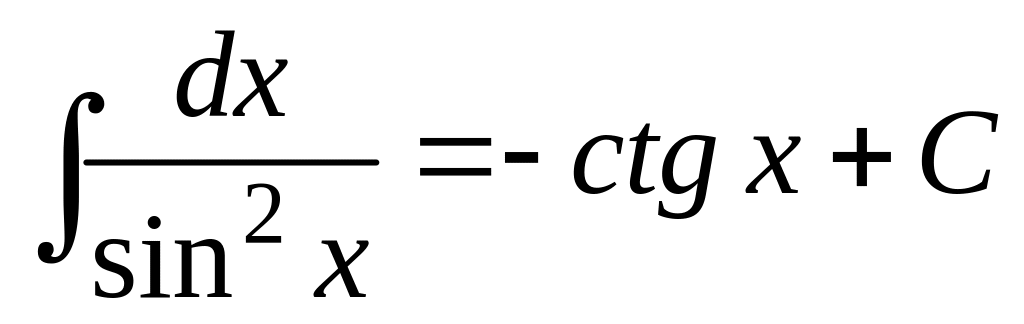 ;
;
3. Замена переменной в интеграле. Примеры.
Пусть требуется найти интеграл , причем непосредственно подобрать первообразную для мы не можем, но нам известно, что она существует.
Сделаем замену
переменной в подынтегральном выражении,
положив
![]() ,
где
,
где
![]()
непрерывная функция с непрерывной
производной, имеющая обратную функцию.
Тогда
непрерывная функция с непрерывной
производной, имеющая обратную функцию.
Тогда
![]() и на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой
и на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой
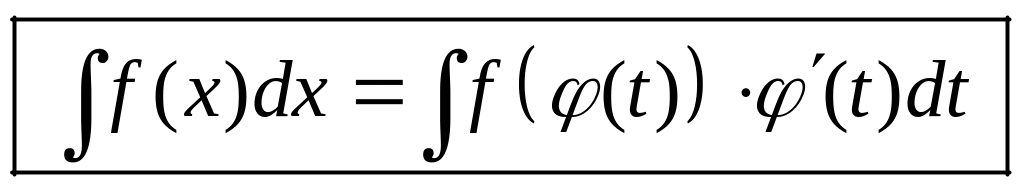 .
.
Иногда целесообразно
подбирать подстановку в виде
![]() ,
тогда
,
тогда
![]() ,
где
.
,
где
.
Другими словами, формулу (2.1) можно применять справа налево.
Пример 2.2. Найти следующие интегралы:
1)
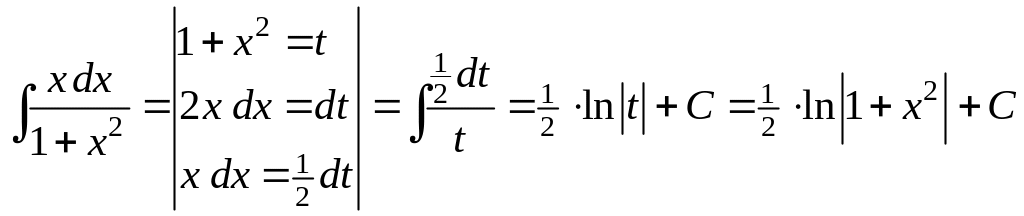 ;
;
3)
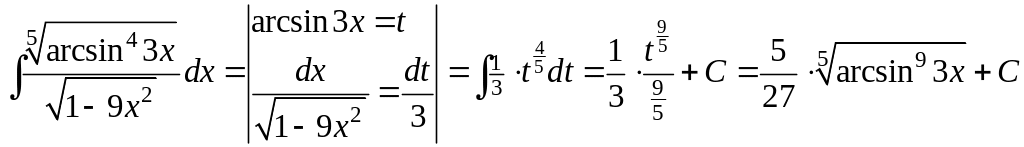 ;
;
