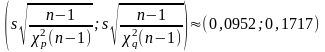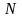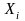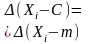Задача 3.7
Имеется выборка, отвечающая нормально распределенной случайной величине .
-
42,22
42,05
41,96
41,86
41,92
41,86
41,91
41,86
41,94
42,08
41,95
41,96
41,92
41,92
41,74
41,93
42,02
42,01
42,28
41,86
42,12
41,98
42,11
42,04
Требуется построить:
1) доверительный интервал для математического
ожидания, соответствующего доверительной
вероятности
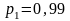 ,
считая, что среднее квадратическое
отклонение случайной величины известно
и равно
,
считая, что среднее квадратическое
отклонение случайной величины известно
и равно
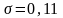 ;
;
2) доверительный интервал математического
ожидания
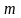 ,
соответствующий доверительной вероятности
,
соответствующий доверительной вероятности
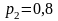 считая, что среднее квадратическое
отклонение неизвестно;
считая, что среднее квадратическое
отклонение неизвестно;
3) доверительные интервалы для дисперсии
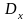 и среднего квадратического отклонения
и среднего квадратического отклонения
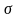 ,
соответствующие доверительной вероятности
,
соответствующие доверительной вероятности
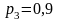 ,
считая, что математическое ожидание
случайной величины
известно и равно
,
считая, что математическое ожидание
случайной величины
известно и равно
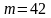 ;
;
4) доверительные интервалы для дисперсии
и среднего квадратического отклонения
,
соответствующие доверительной вероятности
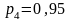 ,
если математическое ожидание неизвестно.
,
если математическое ожидание неизвестно.
Решение:
Сначала найдем
 ,
,
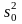 и
и
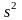 по формулам:
по формулам:
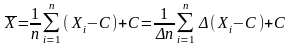
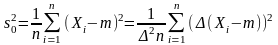

Где множитель
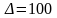 вводится для того, чтобы соответствующие
числа стали целыми.
вводится для того, чтобы соответствующие
числа стали целыми.
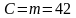 .
Вычисления будем выполнять с помощью
таблицы.
.
Вычисления будем выполнять с помощью
таблицы.
По указанным выше формулам получаем:
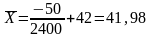
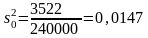 ;
;
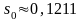
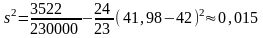 ;
;
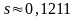
|
|
|
|
|
|
|
|
|
1 |
42,22 |
22 |
484 |
|
14 |
41,92 |
-8 |
64 |
2 |
42,05 |
5 |
25 |
|
15 |
41,74 |
-26 |
676 |
3 |
41,96 |
-4 |
16 |
|
16 |
41,93 |
-7 |
49 |
4 |
41,86 |
-14 |
196 |
|
17 |
42,02 |
2 |
4 |
5 |
41,92 |
-8 |
64 |
|
18 |
42,01 |
1 |
1 |
6 |
41,86 |
-14 |
196 |
|
19 |
42,28 |
28 |
784 |
7 |
41,91 |
-9 |
81 |
|
20 |
41,86 |
-14 |
196 |
8 |
41,86 |
-14 |
196 |
|
21 |
42,12 |
12 |
144 |
9 |
41,94 |
-6 |
36 |
|
22 |
41,98 |
-2 |
4 |
10 |
42,08 |
8 |
64 |
|
23 |
42,11 |
11 |
121 |
11 |
41,95 |
-5 |
25 |
|
24 |
42,04 |
4 |
16 |
12 |
41,96 |
-4 |
16 |
|
|
|
|
|
13 |
41,92 |
-8 |
64 |
|
|
- |
-50 |
3522 |
По таблице II приложения
находим для
квантиль
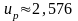 нормального распределения уровня
нормального распределения уровня
 .
Теперь можно построить доверительный
интервал, соответствующий доверительной
вероятности
,
для математического ожидания при
известном
.
Теперь можно построить доверительный
интервал, соответствующий доверительной
вероятности
,
для математического ожидания при
известном
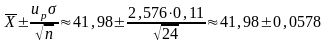
Для построения доверительного интервала
для математического ожидания при
неизвестном
найдем по таблице V
приложения квантиль уровня
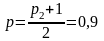 распределения Стьюдента с
распределения Стьюдента с
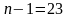 степенями свободы:
степенями свободы:
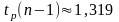 .
Соответствующий доверительный интервал
будет иметь вид:
.
Соответствующий доверительный интервал
будет иметь вид:
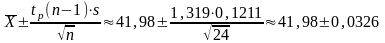
Чтобы построить доверительные интервалы
для дисперсии и среднего квадратического
отклонения при известном математическом
ожидании, найдем по таблицам III
и IV приложения квантили
распределения
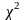 с
с
 степенями свободы уровней
степенями свободы уровней
 и
и
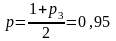 ;
имеем
;
имеем
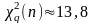 ,
,
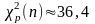
Доверительные интервалы для дисперсии и среднего квадратического отклонения имеют соответственно вид:


Для доверительной вероятности
найдем квантили распределения
с
степенями свободы уровней
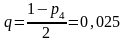 и
и
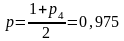 ;
имеем
;
имеем
 ,
,
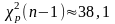 .
Отсюда получаем доверительные интервалы
для дисперсии
и среднего квадратического отклонения
при неизвестном математическом ожидании:
.
Отсюда получаем доверительные интервалы
для дисперсии
и среднего квадратического отклонения
при неизвестном математическом ожидании: