Задача 2.7
По результатам наблюдений над случайной
величиной
,
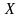распределенной равномерно на интервале
(
),
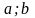получен следующий группированный
статистический ряд:
Интервал
|
61- 62 |
62- 63 |
63- 64 |
64- 65 |
65- 66 |
66- 67 |
67- 68 |
68- 69 |
69- 70 |
70- 71 |
71- 72 |
Частота
|
16 |
27 |
16 |
23 |
17 |
25 |
16 |
20 |
19 |
18 |
3 |
Требуется с помощью метода моментов
получить точечные оценк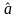и
и
параметров
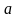и
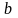и изобразить гистограмму, отвечающую
данному статистическому ряду, и
сглаживающую ее кривую распределения
случайной величины, распределенной
равномерно на интервале (
)
Решение:
Объем выборки составляет 200 элементов. Объединим интервалы, в которые попало «мало» элементов выборки: два последних. Статистический ряд примет вид:
Интервал
|
61- 62 |
62- 63 |
63- 64 |
64- 65 |
65- 66 |
66- 67 |
67- 68 |
68- 69 |
69- 70 |
70- 72 |
Частота
|
16 |
27 |
16 |
23 |
17 |
25 |
16 |
20 |
19 |
21 |
Найдем относительные частоты и оценки
математического ожидания и дисперсии
случайной величины
;
для удобства вычисления оформляем в
виде таблицы. Обозначим через
середину интервала
,
.
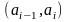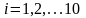В качестве ложного нуля возьмем середину
среднего интервала
.
|
|
|
|
|
|
|
61,5 |
16 |
0,08 |
-5 |
-80 |
25 |
400 |
62,5 |
27 |
0,135 |
-4 |
-108 |
16 |
432 |
63,5 |
16 |
0,08 |
-3 |
-48 |
9 |
144 |
64,5 |
23 |
0,115 |
-2 |
-46 |
4 |
92 |
65,5 |
17 |
0,085 |
-1 |
-17 |
1 |
17 |
66,5 |
25 |
0,125 |
0 |
0 |
0 |
0 |
67,5 |
16 |
0,08 |
1 |
16 |
1 |
16 |
68,5 |
20 |
0,1 |
2 |
40 |
4 |
80 |
69,5 |
19 |
0,095 |
3 |
57 |
9 |
171 |
71 |
21 |
0,105 |
4,5 |
94,5 |
20,25 |
425,25 |
|
200 |
- |
- |
-91,5 |
- |
1777,25 |
Отсюда
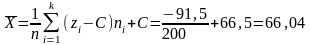
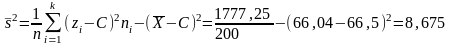
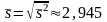
Таким образом,
,
.
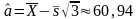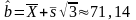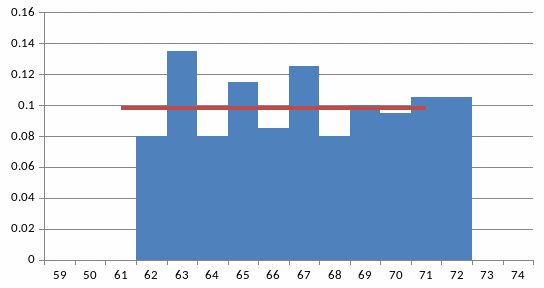
Гистограмма, отвечающая исходному
статистическому ряду, и сглаживающая
ее кривая распределения случайной
величины, распределенной равномерно
на интервале (
),
изображены соответственно на рисунке
(плотность вероятности
).
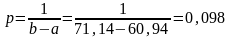