12. Интегральная теорема Коши для односвязной и многосвязной областей. Интегральная формула Коши. Интеграл Коши, его свойства. Существование производных любого порядка у аналитической функции.

Теорема 15.1 (Коши для многосвязной области). Интеграл по за­мкнутому контуру от аналитической функции в многосвязной обла­сти равен 0.

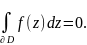
Пусть функция аналитична в замкнутой односвязной област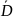и и 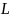– граница области D. Тогда имеет место формула

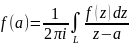
Где точка 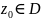– любая точка внутри области D, а интегрирование по контуру L производится в положительном направлении (т.е. против часовой стрелки). Интеграл в правой части называется интегралом Коши

Формула для интегрального представления производных высших по­рядков функции получается дифференцированием (32) под знаком интеграла:

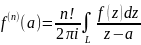
13. Разложение функции, аналитической в круге в степенной ряд. Оценка коэффициентов степенного ряда. Формула Коши для n-ой производной аналитической функции. Теорема Лиувилля.

имеет место равенство

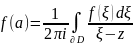
Преобразуем:

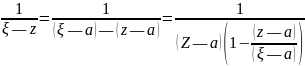
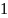
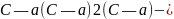
Почленное интегрирование дает ряд Тейлора функции :

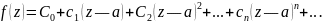
где

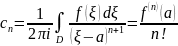
Из приведенных выше преобразований следует, что радиус сходимости

ряда Тейлора равен расстоянию от 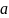до ближайшей особой точки, т. е. точки в которой нарушается аналитичность функции .

Предложение 17.1. Пусть 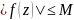на окружности 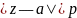радиуса р. Тогда .

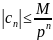Теорема 17.2 (Лиувилля). Аналитическая и ограниченная на всей комплексной плоскости функция может быть только константной.

14. Ряды Лорана. Теорема Лорана.

Всякая аналитическая функция в кольце 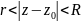функция может быть разложена в этом кольце в ряд

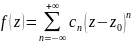
Коэффициенты которого определяются формулой

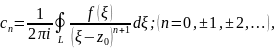
Где L- произвольная окружность с центром в точке лежащая внутри данного кольца.

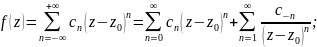
Где первое слагаемое называется правильной частью ряда Лорана(этот ряд сходится внутри круга 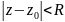), а второе главной частью(этот ряд сходится вне круга ).

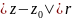15. Изолированные особые точки. Их исследование с помощью ряда Лорана. Особенности на бесконечности.

Особая точка функции комплексного переменного это точка в которой отсутствует аналитичность. Особая точка функции называется изо­лированной, если в некоторой окрестности этой точки функция не имеет других особых точек. Пусть - особая точка, и R - расстояние от a до ближайшей особой точки. Разложим в ряд Лорана в кольце 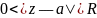. Рассмотрим три случая.

Случай 1. В ряде Лорана главная часть отсутствует.

Тогда, доопределяя функцию f (z) в точке a посредством равенства 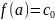, получаем аналитическую в точке a функцию, которую также будем обозначать через . Точка a в этом случае называется устра­нимой особой точкой.

Случай 2. Главная часть ряда Лорана ненулевая и содержит конечное число слагаемых.

Имеем:

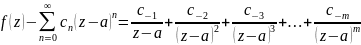
где 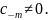В этом случае a называется полюсом порядка m. Если m = 1, то a называется простым полюсом

Случай 3. Главная часть ряда Лорана содержит бесконечное число слагаемых. В этом случае a называется существенной особой точкой.

Теорема 19.6 (Ю.В. Сохоцкого). Если a - существенная особая точ­ка функции , то для любого 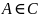или 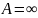найдется последо­вательность такая, что .

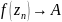16. Вычет. Вычисление вычета в полюсе.

Определение 20.1. Пусть в проколотой окрестности точки a функция f (z) аналитична. Тогда величину

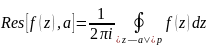
где р - достаточно малое положительное число, будем называть вычетом

функции в точке .

Вычетом функции относительно бесконечно удаленной точки считаем

величину

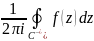
где C - окружность с центром в начале координат такая, что вне круга, определяемого этой окружностью, функция особенностей не имеет.

Первичные следствия этого определения следующие:

1) вычет не зависит от величины р;

2) вычет совпадает с коэффициентом 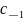ряда Лорана функции в кольце

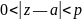
3) если аналитична в точке или - устранимая особенность, то вычет в ней равен 0.

Предложение 20.2. Пусть a - полюс порядка m функции . Тогда

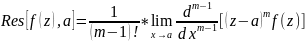
Отметим частный случай простого полюса

Предложение 20.3. Пусть a - простой полюс функции f (z). Тогда

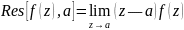
В частности, если 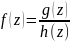, где 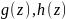аналитичны в окрестно­сти точки 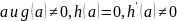, то a - простой полюс и

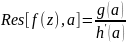
17. Основная теорема о вычетах. Применение вычетов к вычислению интегралов.

Теорема 20.4 (основная о вычетах). Пусть f (z) аналитична в за­мкнутой области D, кроме точек a₁,a₂,.., a_m, лежащих внутри обла­сти D. Тогда

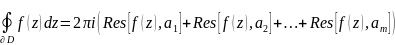
Предложение 21.1. Предположим, что бесконечно удаленная точка является нулем второго или более высокого порядка функции , т.е. разложение в ряд Лорана в окрестности ж имеет вид

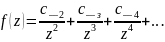
Допустим также, что является аналитической функцией на дей­ствительной оси, а в верхней полуплоскости 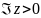имеет лишь конечное число особых точек 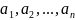. Тогда