
- •1. Комплексное число, действительная и мнимая части, равенство комплексных чисел. Сложение и умножение комплексных чисел. Поле комплексных чисел, формула обращения ненулевого комп. Числа.
- •4. Пополнение поля компл. Чисел бесконечно удалённой точкой.
- •5. Функции компл. Переменного. Предел и непрерывность. Области на компл. Плоскости (ограниченные, открытые, замкнутые, связные, односвязные, многосвязные). Граница области.
- •6. Степенные ряды (по степеням (z – a)). Теорема Абеля. Радиус сходимости и круг сходимости. Аналитичность суммы степенного ряда.
- •7. Производная функции комплексного переменного, аналитичность в точке и области. Геометрический смысл производной, сохранение углов. Свойства производных.
- •12. Интегральная теорема Коши для односвязной и многосвязной областей. Интегральная формула Коши. Интеграл Коши, его свойства. Существование производных любого порядка у аналитической функции.
- •1. Изображение Лапласа, оригинал, ограничения на оригинал, показатель роста. Аналитичность изображения. Теорема единственности.
- •2. Функция Хевисайда, её изображение. Теорема подобия. Свойство линейности оператора Лапласа. Смещение изображения. Теорема запаздывания.
- •7. Биноминальное распределение.
- •8. Распределение Пуассона.
- •9. Геометрическое распределение (вероятность первого успеха)
- •10. Математическое ожидание. Определение мат. Ожидания. Свойства мат. Ожидания. Вычисление мат. Ожидания биноминального распределения , распределения Пуассона и геометрического распределения.
- •Основные свойства математического ожидания:
- •Свойства дисперсии:
- •13.Определение и свойства математического ожидания, дисперсии и среднего квадратичного отклонения непрерывной случайной величины.
1. Комплексное число, действительная и мнимая части, равенство комплексных чисел. Сложение и умножение комплексных чисел. Поле комплексных чисел, формула обращения ненулевого комп. Числа.
Комплексное
число отличается от действительного
тем, что у него имеется помимо действительной
еще и мнимая часть.
 .
Такие числа равны если равны их
действительные и мнимые части. Сложение:
.
Такие числа равны если равны их
действительные и мнимые части. Сложение:
 то
есть складываются действительная с
действительной, а мнимая с мнимою.
Умножение происходит аналогично простому
раскрытию скобок:
то
есть складываются действительная с
действительной, а мнимая с мнимою.
Умножение происходит аналогично простому
раскрытию скобок: Полем комплексных чисел С называется
поле содержащее R
в качестве подполя в котором уравнение.
Полем комплексных чисел С называется
поле содержащее R
в качестве подполя в котором уравнение.
 имеет корень.
имеет корень.
Формула
обращения комплексного числа в
тригонометрическую форму:

2. Сопряжение, его геометрический смысл, свойства. Аргумент и модуль компл. числа. Тригонометрическая и показательная формы записи компл. чисел.
Число
 называется комплексно сопряженным с
.
Отображение
называется комплексно сопряженным с
.
Отображение
 называется сопряжением. Геометрически
это отражение относительно действительной
оси. Модулем
называется сопряжением. Геометрически
это отражение относительно действительной
оси. Модулем
 называют
квадратный корень из нормы(
называют
квадратный корень из нормы( )
комплексного числа
)
комплексного числа
 .
Аргументом комплексного числа называют
угол между вектором комплексного числа
и осью действительных чисел.
Тригонометрическая форма.
Показательная:
.
Аргументом комплексного числа называют
угол между вектором комплексного числа
и осью действительных чисел.
Тригонометрическая форма.
Показательная:


3. Извлечение корней из компл. чисел. Решение квадратных уравнений над полем С. Основная теорема алгебры.
Нам
дано уравнение:
 где z
– неизвестная. Запишем его в показательной
форме. Где
где z
– неизвестная. Запишем его в показательной
форме. Где
 т.е.
т.е.
 Подставляя вместо
Подставляя вместо
 значения 0,1,2… n-1
Если
значения 0,1,2… n-1
Если
 то
корни уравнения:
то
корни уравнения:

Решение
квадратного уравнения
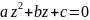 имеет такой же алгоритм, как и для
действительных чисел, за тем исключением,
что здесь корни есть всегда. Основная
теорема алгебры: Всякий
многочлен с любыми комплексными
коэффициентами , степень которого не
меньше единицы имеет хотя бы один корень,
в общем случае комплексный.
имеет такой же алгоритм, как и для
действительных чисел, за тем исключением,
что здесь корни есть всегда. Основная
теорема алгебры: Всякий
многочлен с любыми комплексными
коэффициентами , степень которого не
меньше единицы имеет хотя бы один корень,
в общем случае комплексный.
4. Пополнение поля компл. Чисел бесконечно удалённой точкой.
Если
дано подмножество М и оно лежит внутри
круглого комплексного поля с радиусом
R,
то внешность этого круга является
окрестностью бесконечно удаленной
точки. Бесконечно удаленная точка
позволяет проводить следующие операции.
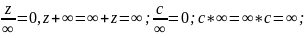 Поле
комплексных чисел пополненное бесконечно
удаленной точкой называется расширенной
комплексной плоскостью. Графически она
изображается сферой Римана, где бесконечно
удаленные точки являются северным и
южным полюсами этой сферы.
Поле
комплексных чисел пополненное бесконечно
удаленной точкой называется расширенной
комплексной плоскостью. Графически она
изображается сферой Римана, где бесконечно
удаленные точки являются северным и
южным полюсами этой сферы.
5. Функции компл. Переменного. Предел и непрерывность. Области на компл. Плоскости (ограниченные, открытые, замкнутые, связные, односвязные, многосвязные). Граница области.
Функцию
комплексного переменного можно записать
в виде
 где
где
 действительная
часть,
действительная
часть,
 мнимая
часть. Пусть
мнимая
часть. Пусть
 определена в окрестности точки
определена в окрестности точки
 ,
кроме может быть самой
,
кроме может быть самой
 Предел функции
Предел функции
 При
При
 равен А принадлежащему С, если для любого
действительного числа
равен А принадлежащему С, если для любого
действительного числа
 найдется число
найдется число
 такое, что для всех точек z
из проколотой окрестности, т.е. для точек
с условием
такое, что для всех точек z
из проколотой окрестности, т.е. для точек
с условием
 ,
выполняется неравенство
,
выполняется неравенство
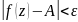 .
.
Как
и для действительной переменной, функция
комплексной переменной
непрерывна в точке
,
если она определена в окрестности этой
точки и
 .
.
При
определении предела функции или
последовательности важную роль играет
понятие окрестности точки
.
Во-первых, определим "стандартную"
окрестность - круг без границы радиуса с центром в точке
.
Он задается неравенством
с центром в точке
.
Он задается неравенством
 .
В общем,
окрестностью точки z0
называется
любое открытое множество комплексных
чисел, содержащее точку
z0.
При
этом подмножество
.
В общем,
окрестностью точки z0
называется
любое открытое множество комплексных
чисел, содержащее точку
z0.
При
этом подмножество
 называется
открытым,
если вместе с каждой точкой множество
G
содержит
и круг достаточно малого радиуса с
центром в этой точке. Подмножество
называется
открытым,
если вместе с каждой точкой множество
G
содержит
и круг достаточно малого радиуса с
центром в этой точке. Подмножество
 называется
замкнутым,
если дополнение
называется
замкнутым,
если дополнение
 открыто,
т. е. если для любой точки
открыто,
т. е. если для любой точки
 найдется
число
р >
0 такое, что круг
не пересекается с D.
найдется
число
р >
0 такое, что круг
не пересекается с D.
Область D называется связной, если для любых ее точек z1 и z2 найдется непрерывный путь L, целиком лежащий в этой области и соединяющий точки z1 и z2. Более жесткое требование - односвязность области, тот случай когда граница области одна непрерывная кусочно гладкая кривая. Примером связной, но не односвязной области является кольцо.
Многосвязная область это область, в которой существуют замкнутые кривые, не стягиваемые в пределах этой области в точку.
Граница области - совокупность всех граничных точек. Граничная точка множества, точка, в любой окрестности которой находятся как точки, принадлежащие данному множеству, так и не принадлежащие ему. В случае открытых множеств, т. е. множеств, каждая точка которых обладает окрестностью, содержащейся в этом множестве, Граничная точка не принадлежит самому множеству.
