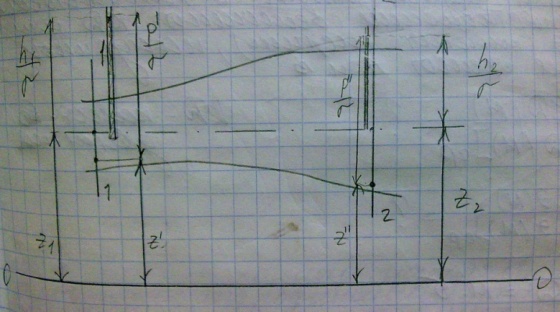
- •29. Параллельноструйные, плавно изменяющиеся и резко изменяющиеся движения жидкости. Живое сечение, расход и средняя скорость. Эпюра скоростей.
- •31.Уравнение несжимаемости движущейся жидкости в дифференциальной форме.
- •3 2.Неравномерное и равномерное движение. Напорное и безнапорное движения, свободные струи. Гидравлические элементы живого сечения.
- •33. Ур. Бернулли для элементарной струйки идеальн. Жид-ти при установившемся движ-ии.
- •34.Значения трёх слагаемых входящих в ур. Бернулли. Геометрич. Интерпретация ур-ия для элементарной струйки идеальной жид-ти.
34.Значения трёх слагаемых входящих в ур. Бернулли. Геометрич. Интерпретация ур-ия для элементарной струйки идеальной жид-ти.
1) Координата z наз. отметкой: z представляет собой возвышение рассматриваемого живого сечения струйки над горизонтальной плоскостью ОО, котор. наз плоскостью сравнения. 2) Член представляет собой пьезометрическую высоту, отвечающую гидродинамическому давлению р в точке. Можно сказать, что явл. высотой столба жид-ти в пьезометре, приключенном к живому сечению струйки. 3) Член u2/2 наз. скоростным напором. Размерность этого слагаемого, так же как и размерность двух других слагаемых, линейная. [u2/2 ]=[L2]/[t2]: [L]/[t2]=[L], где L-символ длины; t-символ времени. Известно, что величина u2/2 предст. собой высоту, с которой в пустоте должно свободно упасть тело, чтобы приобрести скорость u. Величина u2/2 м.б. измерена при помощи трубки Пито, у котор. нижний конец загнут так, чтобы скорость u была направлена во входное отверстие трубки.
Г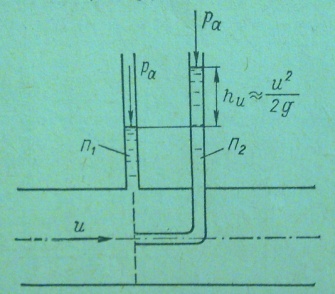 оризонт
воды в трубке П2
устанавливается выше горизонта воды
в трубке П1
на величину hu=
u2/2
.
Измерив величину hu,
находим скорость u
в рассматриваемой точке: u=
оризонт
воды в трубке П2
устанавливается выше горизонта воды
в трубке П1
на величину hu=
u2/2
.
Измерив величину hu,
находим скорость u
в рассматриваемой точке: u=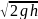 или u=φ
,
где φ-поправочный коэф-т, который
находится для данной трубки Пито путём
ее тарирования.
или u=φ
,
где φ-поправочный коэф-т, который
находится для данной трубки Пито путём
ее тарирования.
Г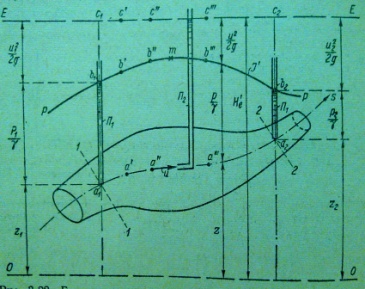 еометрич.
интерпретация:
еометрич.
интерпретация:
1)линия
Р-Р, проходящая по точкам b
и, следовательно, возвышающаяся на
величину
над осью струйки, наз. пьезометрической
линией. Можно сказать,что эта линия
проходит по горизонтам жид-ти в
пьезометрах Пi.
2) Линия Е-Е, проходящая по точкам с
и, следовательно, возвышающаяся над
линией Р-Р на величину скоростного
напора, наз. напорной линией. Эта линия
проходит по горизонтам жид-ти в трубках
Пито П2,
установленных вдоль оси струйки.
3)Пьезометрическим уклоном J’
струйки в данном её сечении наз.
элементарное падение пьезометрич.
линии Р-Р, отнесённое к соответствующей
элементарной длине (ds)
струйки: J’=
-
 .
4)Полный напор Н’e
представляет собой сумму трёх членов:
Н’e=z+
.
4)Полный напор Н’e
представляет собой сумму трёх членов:
Н’e=z+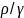 +
u2/2
+
u2/2
35.Гидравлическое уравнение кинетической энергии, уравнение Бернулли для элементарной струйки реальной жидкости. Реальная вязкая жидкость характеризуется наличием сил трения кот. возникают при её движении. Силы трения в потоке жидкости играют двоякую роль:
1.Благодаря силе трения часть мех энергии переходит в тепло, что способствует уменьшению мех энергии вдоль струйки.
2.наличие силы между отдельными струйками создающие такие условия при кот. мех. энергия 1-й струйки переходит 2-й струйке, т.е. диффузия мех. энергии.
Учитывая
всё сказанное понимаем что мех. энергия
элементарной струйки реальной жидкости
вдоль течения изменяется He1=He2+∆hf+∆hдиф,
где ∆hfпотеря
энергии на трение – потеря полного
напора, ∆hдиф
-
диффузионные потери. Для некоторых
струек ∆hдиф=0
следовательно, уравнение Бернулли для
элементарной струйки реальной жидкости
будет записываться так z1+ +υ21/2g=
z2+
+υ21/2g=
z2+ +υ22/2g+∆hf.
+υ22/2g+∆hf.
36.Энергетическая интерпретация ур. Бернулли. Распределение давления в живых сечениях потока. Рассмотрим три слагаемых, составляющих полный напор, с энергетической точки зрения. Первые два слагаемых представляют собой потенциальный напор: H=z + . Третье слагаемое u2/2 – скоростной напор- представл. собой удельную кинетич. энергию. (КЭ)=Mu2/2. Удельная кинетич. энергия: (УКЭ)=(КЭ)/вес=(КЭ)/Mg= Mu2/2 Mg= u2/2g. Энергетическое выражение полного напора м ожно представить в виде: Н’e=z+ + u2/2 =УЭ полная.
Рассмотрим случай установившегося движ. и здесь действуют только силы тяжести: