
- •29. Параллельноструйные, плавно изменяющиеся и резко изменяющиеся движения жидкости. Живое сечение, расход и средняя скорость. Эпюра скоростей.
- •31.Уравнение несжимаемости движущейся жидкости в дифференциальной форме.
- •3 2.Неравномерное и равномерное движение. Напорное и безнапорное движения, свободные струи. Гидравлические элементы живого сечения.
- •33. Ур. Бернулли для элементарной струйки идеальн. Жид-ти при установившемся движ-ии.
- •34.Значения трёх слагаемых входящих в ур. Бернулли. Геометрич. Интерпретация ур-ия для элементарной струйки идеальной жид-ти.
29. Параллельноструйные, плавно изменяющиеся и резко изменяющиеся движения жидкости. Живое сечение, расход и средняя скорость. Эпюра скоростей.
Можно различать частные случаи потока, когда линии тока его являются строго параллельными прямыми. Такое движение жидкости называем параллельноструйным. Однако, часто приходится сталкиваться с потоками, отличными от параллельноструйного. Рассматривая такого рода потоки, различаем так называемые плавно изменяющиеся и резко изменяющееся движение. Плавно изменяющимся движением называется движение, близкое к параллельноструйному. При плавно изменяющемся движении поток должен удовлетворять след. 2м условиям:
1.Радиус кривизны линии тока должен быть весьма велик
2.Угол образованный линиями тока должен быть близок к нулю.
При несоблюдении двух этих условий или одного из них получаем движение называемое резко изменяющимся.
Живое сечение. Представим поток жидкости и покажем внутри потока линии тока.
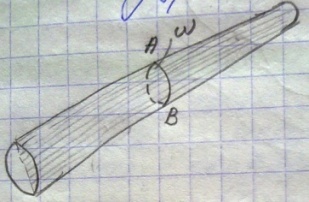
Проведём к этим линиям тока поверхность АВ. Поверхность АВ нормальна к линиям тока и лежащая внутри потока наз. живым сечением(ω).

 Расход
жидкости – объём
её приходящий в единицу времени через
живое сечение обозначается Q. Размерность
[м3/с].
Q=Udω,
Q=
Расход
жидкости – объём
её приходящий в единицу времени через
живое сечение обозначается Q. Размерность
[м3/с].
Q=Udω,
Q= .
Средняя
скорость. Из
вышеизложенного в точках живого сечения
скорость U и скорость U1≠U2≠U3≠…
При параллельноструйным
течении вводится понятие средней
скорости для данного сечения(и она
фиктивна). υ=Q/ω,
υ=
.
Средняя
скорость. Из
вышеизложенного в точках живого сечения
скорость U и скорость U1≠U2≠U3≠…
При параллельноструйным
течении вводится понятие средней
скорости для данного сечения(и она
фиктивна). υ=Q/ω,
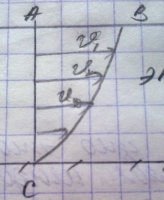
υ= . Эпюра
скоростей.
. Эпюра
скоростей.
30. Уравнение неразрывности (или сплошности) движущейся жидкости в случае установившегося движения. *Случай резко изменяющегося движения жидкости. Представим поток жидкости и наметим два его живых сечения(1-1, 2-2), рассмотрим отсек abcd заключений между этими сечениями и ограниченными с боков поверхностью АВ образованной линиями тока.
Б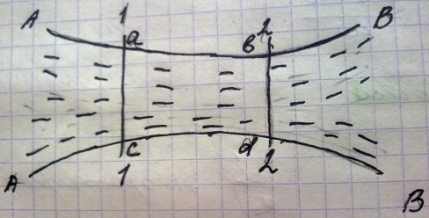 удем
считать что этот отсек принадлежит
пространству и является неподвижным,
жидкость протекает через него. Обозначим
через Q1
и Q2
;соответственно расход в сечении 1-1 и
2-2, за время dt
в
этот отсек через живое сечение 1-1
поступит объём жидкости равный Q1dt
а выйдет через сечение 2-2 Q2dt
Учтем следующие
3-и
обстоятельства:
удем
считать что этот отсек принадлежит
пространству и является неподвижным,
жидкость протекает через него. Обозначим
через Q1
и Q2
;соответственно расход в сечении 1-1 и
2-2, за время dt
в
этот отсек через живое сечение 1-1
поступит объём жидкости равный Q1dt
а выйдет через сечение 2-2 Q2dt
Учтем следующие
3-и
обстоятельства:
1.Проникновение жидкости через боковую поверхность АВ отсека abcd невозможна.
2.Жидкость является несжимаемой
3.Жидкость движется сплошным потоком без образования разрывов. Q1dt= Q2dt= Q=const(по течению).
*Случай плавно изменяющегося движения жидкости. В этом случае оперируют плоскими живыми сечениями причём здесь Q=ωυ. Имея это ввиду для плавно изменяющегося уравнения неразрывности Q=ωυ=const(по течению) можно записать в виде ω1/ω2=υ1/υ2 (для 2-х сечений).


31.Уравнение несжимаемости движущейся жидкости в дифференциальной форме.
Представим оси координат X, Y, Z, возьмём неподвижную точку пространства А определяемую координатами X, Y, Z.
U-скорость, Ux, Uy, Uz-проекции.
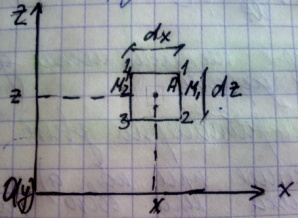
Составляющие
скорости U в т.А для определённого
момента времени dt обозначим Ux,
Uy,
Uz
выделим элементарный объём у т.А в форме
параллепипеда 1234 бесконечно малые
длины его сторон обозначим через dx, dy,
dz. Определим объём жидкости поступающий
в него за время dt
и объём жидкости вышедший из него за
время dt. δW1-вышедшее
количество воды. δW1=(UМ(1))xdzdydt=(Ux+ )dxdydzdt.
δW2-вошедшее
количество воды. δW2=(Ux-
)dxdydzdt,
δW=
δW1-
δW2=
)dxdydzdt.
δW2-вошедшее
количество воды. δW2=(Ux-
)dxdydzdt,
δW=
δW1-
δW2=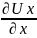 dxdydzdt,
δW=
(δW1-
δW2)+(δW3-
δW4)+(δW5-
δW6)=0.
Подставив в эту зависимость и сокращая
на dxdydzdt
получим
=
dxdydzdt,
δW=
(δW1-
δW2)+(δW3-
δW4)+(δW5-
δW6)=0.
Подставив в эту зависимость и сокращая
на dxdydzdt
получим
=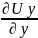 =
=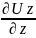 =0.
Это и есть уравнение несжимаемости
однордной жидкости в дифференциальной
форме.
=0.
Это и есть уравнение несжимаемости
однордной жидкости в дифференциальной
форме.
