25. Атом водорода. Общая формула Бальмера.

Атом водорода — физическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра может входить протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон преимущественно находится в тонком концентрическом шаровом слое вокруг атомного ядра, образуя электронную оболочку атома. Наиболее вероятный радиус электронной оболочки атома водорода в стабильном состоянии равен боровскому радиусу a0 = 0,529 Å.

Строение и свойства атома водорода.

Образование атома водорода и его спектр излучения

При попадании в электрическое поле положительно заряженного протона отрицательно заряженного электрона происходит захват последнего протоном — образуется атом водорода. Образовавшийся атом водорода находится в возбуждённом состоянии. Время жизни атома водорода в возбуждённом состоянии — ничтожные доли секунды (10−8 — 10−10сек)[1], однако очень высоковозбуждённые атомы в бесстолкновительной среде могут существовать до секунд. Снятие возбуждения атома происходит за счёт излучения фотонов с фиксированной энергией, проявляющихся в характерном спектре излучения водорода. Поскольку газообразный атомарный водород содержит множество атомов в различных степенях возбуждения, спектр состоит из большого числа линий.

Линии спектра серии Лаймана обусловлены переходом электронов на нижний уровень с квантовым числом n = 1 с уровней с квантовыми числами n = 2, 3, 4, 5, 6… Линии Лаймана лежат в ультрафиолетовой области спектра. Линии спектра серии Бальмера обусловлены переходом электронов на уровень с квантовым числом n = 2 с уровней с квантовыми числами n = 3, 4, 5, 6… и лежат в видимой области спектра.

Линии спектра серий Пашена, Брэкета и Пфунда обусловлены переходом электронов на уровни с квантовыми числами n, равными 3, 4 и 5 (соответственно), и расположены в инфракрасной области спектра.[3].

В нормальном (основном) состоянии (главное квантовое число n = 1) атом водорода в изолированном виде может существовать неограниченное время. Согласно квантохимическим расчетам, радиус мест наибольшей вероятности нахождения электрона в атоме водорода в нормальном состоянии (главное квантовое число n = 1) равен 0,529 Å. Этот радиус является одной из основных атомных констант, он получил название боровский радиус (см. выше). При возбуждении атома водорода электрон проходит на более высокий квантовый уровень (n = 2, 3, 4 и т. д.), при этом радиус мест наибольшей вероятности нахождения электрона в атоме возрастает пропорционально квадрату главного квантового числа: rn = a0 · n2.

Се́рия Ба́льмера — спектральная серия, наблюдающаяся для атомов водорода. Названа в честь швейцарского физика Иоганна Бальмера , описавшего в 1885 году эту серию формулой.

где n = 3, 4, 5, 6; b = 3645,6 Å

26. Квантовая механическая задача об атоме водорода.

27. Квантовые числа m, n, l. Графическое представление энергитических параметров.

Квантово-механическая теория атома, построенная на уравнении Шредингера, гораздо совершеннее полу‑классичекой теории атома Бора, построенной на ряде постулатов. Она сохраняет некоторые аспекты старой теории – например, электроны могут находиться в атоме только в состояниях с определенной дискретной энергией; при переходе электрона из одного состояния в другое испускается (или поглощается) фотон. Но квантовая механика не просто дополняет теорию Бора, она рисует совершенно иную картину строения атома. Согласно квантовой механике, не существует определенных круговых орбит у электронов, как в теории Бора. В силу волновой природы электрон «размазан» в пространстве, т.е. может с определенной вероятностью находится в любой точке пространства.

При рассмотрении атома водорода, движение его единственного электрона можно рассматривать как движение в электрическом поле ядра. По аналогии с задачей о движении частицы в потенциальной яме простой формы, здесь необходимо найти решения стационарного уравнения Шредингера в трехмерном пространстве с конкретным видом потенциальной энергии, описывающем его электростатическое взаимодействие с ядром

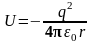. (2.1)

При решении уравнения Шредингера в данном случае используют специальные функции математической физики - сферические функции и сферическую систему координат, центр которой совпадает с центром ядра атома. Если записать уравнение Шредингера в сферических координатах (r, , ), то его можно строго аналитически решить, это решение представляют в виде произведения трех функций

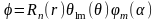(2.2)

Важной особенностью решения является его зависимость от трех чисел n, l, m, называемых квантовыми числами. В квантовой механике каждому решению соответствует определенное состояние атома со своим распределением электрона вокруг ядра, которое задается соответствующей волновой функцией, зависящей от трех квантовых чисел: n, l, m_.

Квантовое число n называется главным квантовым числом, от него зависит значение полной энергии атома водорода, при этом атом может иметь не любые значения энергии Е, а лишь некоторые Е_n. Квантовое число n может принимать следующий ряд значений n = 1, 2, 3, … . Значения энергии Е_n, которые может иметь атом, называют разрешенными значениями энергии атома, а их совокупность Е₁, Е₂, … Е_ представляет собой энергетический спектр атома. Разрешенные значения энергии обычно изображаются в виде горизонтальных линий, называемых энергетическими уровнями. Для атома водорода квантовая механика предсказывает точно такие же энергетические уровни, что и теория Бора, т.е.

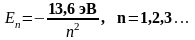. (2.3)

Состояние атома с наименьшей энергией называется основным (n = 1), все остальные состояния – возбужденными (см. рис.8).

Рис.8. Схема энергетических уровней атома водорода.

Орбитальное квантовое число l связано с моментом импульса орбитального движения электрона вокруг ядра. Так как электрон имеет электрический заряд, то его движение вокруг ядра приводит к появлению магнитного момента, аналогичного магнитному моменту кругового витка с током. Орбитальное квантовое число l может принимать целочисленные значения от 0 до n -1, оно квантует величину момента импульса L и магнитного момента  согласно соотношениям

, (2.4)

где _Б - постоянная, служащая единицей измерения магнитных моментов атомов и называемая магнетоном Бора. Сравнивая формулу квантования момента импульса с формулой квантования в теории Бора, можно заметить, что они не совпадают. Более того, при l=0, в квантовой механике возможны состояния атома с нулевым моментом импульса электрона. Опыт подтверждает существование квантовых состояний атома с нулевыми орбитальными моментами, хотя при классическом описании движения электрона в атоме по определенной орбите атом должен всегда обладать ненулевым моментом импульса.

Магнитное квантовое число m характеризует ориентацию момента импульса L и магнитного момента  во внешнем силовом поле (например, магнитном или электрическом) и может принимать целочисленные значения от – l до + l . Согласно классической теории магнитный момент всегда стремится повернуться вдоль направления магнитного поля. В квантовой механике движение электрона таково, что магнитный момент может быть направлен в нескольких, строго определенных направлениях в зависимости от состояния атома, то есть он квантуется не только по величине, но и по направлению. Такое пространственное квантование приводит к тому, что проекции момента импульса и магнитного момента электрона на выделенное в пространстве направление могут иметь только строго определенные значения. Ориентацию магнитного момента и момента импульса задают как и в классической физике, указывая его компоненту вдоль оси z, совпадающей с направлением магнитного поля. В квантовой механике возможные проекции L_z и _z определяются магнитным квантовым числом m с помощью соотношений

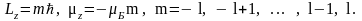(2.5)

Так как формула квантования проекции механического момента соответствует вполне определенным направлениям ориентации в пространстве векторов L и , то эту формулу называют обычно формулой пространственного квантования. С точки зрения классического представления об электронной орбите, эта формула определяет возможные дискретные расположения электронных орбит в пространстве по отношению к направлению внешнего поля. По отношению к другим координатам x и y положение векторов момента импульса L и магнитного момента  меняется так, как если бы они вращались вокруг оси z. Такое вращение называется прецессией (см. Рис. 9).

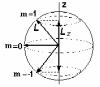
Рис. 9. Пространственное квантование момента импульса для состояния l =1 и траектории прецессии.