Уравнение Шредингера. Физические ограничения на вид волновой функции. Стационарное уравнение Шредингера, стационарные состояния.

Для расчета волновой функции необходимо иметь уравнение, которое позволяло бы для любого момента времени определить эту функцию с учетом действующих на частицу внешних силовых полей. Чтобы искомое уравнение учитывало волновые свойства микрочастиц, необходимо чтобы оно по форме было волновым уравнением, подобно тем, которые описывают звуковые или электромагнитные волны. Известно, что для плоской волны, распространяющейся вдоль оси х, волновое уравнение – это дифференциальное уравнение в частных производных, где независимыми переменными являются координаты и время. Учитывая такие аналогии, австрийский физик Эрвин Шредингер получил в 1926 г. основное уравнение квантовой механики для ψ (х, у, z, t)

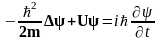, (1.10)

где m – масса частицы, i – мнимая единица, U – потенциальная энергия частицы, Δ‑оператор Лапласа, который представляет собой сумму вторых частных производных по координатам, т.е.

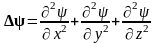(1.11)

Из уравнения Шредингера следует, что конкретный вид волновой функции зависит от потенциальной энергии U, т.е. определяется характером сил, действующих на частицу. Уравнение Шредингера оказалось комплексным (включающим в себя мнимую единицу), поэтому и волновая функция также комплексная, при этом реальный физический смысл имеет квадрат модуля волновой функции (2.5, 2.6), который всегда действителен.

Уравнение Шредингера, будучи дифференциальным уравнением, может иметь множество решений. Из этих решений смысл имеют только те, в которых волновая функция будет однозначной, непрерывной и конечной, что соответствует физической реальности. Эти требования должны относиться и к частным производным от функции по времени и координатам, так как они тоже входят в уравнения Шредингера. Кроме этих требований на волновую функцию накладывается условие нормировки

, (1.12)

которое следует из того факта, что частица реально существует и обязательно находится где-либо в окружающем пространстве. Поэтому суммарная вероятность нахождения частицы во всем бесконечном пространстве равна единице, т.е. это достоверное событие. Смысл и назначение уравнения Шредингера заключается в том, что если известна волновая функция некоторой частицы в начальный момент времени и известно силовое поле, в котором она движется, то, решив это уравнение, можно найти волновую функцию и узнать характеристики состояния частицы в последующие моменты времени.

Если силовое поле, в котором движется частица, постоянно во времени, то U не зависит от времени и волновую функцию можно представить в виде , где Е – полная энергия частицы. Если мы подставим такую функцию в уравнение Шредингера, проведем дифференцирование и сокращение, то получим уравнение

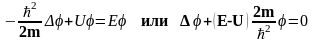(1.13)

Это - уравнение Шредингера для, так называемых, стационарных состояний, находясь в которых частица имеет определенные, не меняющиеся со временем характеристики.