Порядок виконання роботи

1. Розміщують прилади на оптичній лаві (відповідно рис.4) на відстані 5-10 см. Від лазера розміщують щільову діафрагму 2, за нею на відстані 30-40 см біпризму 3, далі на відстані 50-70 см короткофокусну лінзу 4 (№ 2) і на відстані 20 – 30 см від лінзи – екран 5.

Центри усіх розміщених на лаві приладів повинні лежать на однаковій висоті. Кінцеве центрування приладів здійснюють при увімкненому лазері.

2. Вмикають лазер із дозволу викладача або лаборанта.

3. Юстують установку, намагаючись щоб промінь лазера потрапив на щілину 2 і загальну грань призми 3, а смужка, яка світиться, з інтерференційними лініями у пучку променів за біпризмою потрапила в центр короткофокусної лінзи 4. При юстуванні слід пам’ятати, що прямий лазерний промінь ні в якому разі не повинен потрапляти в око або на незахищену шкіру. Трохи пересуваючи вздовж оптичної вісі біпризму 3 і лінзу 4, намагаються, щоб на горизонтальній шкалі екрана 5 спостерігалась виразна картина вертикально розташованих інтерференційних ліній.

4. Вимірюють ширину лінії X. Для цього за допомогою шкали на екрані 5 вимірюють відстань g між серединами світлих (або темних) ліній, що знаходяться на відстані одна від одної m = 5-10 ліній. Ширина лінії X= . Це вимірювання роблять не менш трьох разів і знаходять середнє значення X.

5. За лінійкою, що закріплена на оптичній лаві, знаходять відстані b, c, d.

6. За допомогою отриманих значень b, c, d, X знаходять довжину хвилі випромінювання , використовуючи формулу (14) і вважаючи n=1,5 f= =35,83 мм.

• 7. Змінюючи положення біпризми і лінзи, досягають нової різкої картини інтерференційних ліній на екрані. Повторюють п.п. 4-6 і отримують знов значення .

7. Знаходять середнє значення довжини хвилі лазерного випромінювання за двома незалежними вимірюваннями.

Контрольні запитання.

1. Що таке інтерференція світла?

2. Що таке біпризма Френеля?

3. Намалювати хід променів у біпризмі Френеля.

4. Які хвилі називають монохроматичними?

5. Для чого використовується біпризма Френеля?

Література: [1, 4, 7] .

Лабораторна робота №5 визначення радіуса кривизни лінзи за допомогою кілець ньютона

Мета роботи: Визначити радіус кривизни лінзи за допомогою кілець Ньютона.

Прилади і матеріали: скляна лінза, змонтована з плоско-паралельною пластиною, бінокулярний мікроскоп, один монокуляр якого використовується для підсвічування, а другий має окулярну шкалу, масштабна лінійка з ціною поділки 1 мм, світлофільтр, який пропускає світло визначеної довжини хвилі λ_ж=5860 Å, _ч = 6520 Å, _з = 5460 Å.

Теоретичні відомості

С хема установки показана на рис. 1. Світло від лампи розжарення освітлювача 1, після проходження світлофільтра 2 та об’єктива 3 падає вертикально на лінзу 4, відбивається і спостерігається через окуляр 5. Тобто, цей прилад дозволяє спостерігати кільця Ньютона у відбитому світлі при нормальному падінні променів.

Р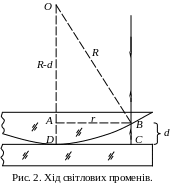 озглянемо хід променів на рис. 2. Промінь світла падає зверху. В точці В світло частково відбивається, а частково проходить далі. У точці С світло також частково відбивається. Світловий промінь поділяється на два промені, які можуть інтерферувати. Спостереження проводяться поблизу точки D, де повітряний проміжок ВС дуже тонкий. Радіус R кривизни лінзи досить великий, тому можна вважати, що відбиті промені поширюються вверх в одному напрямі.

Якщо оптична різниця шляхів цих променів дорівнює цілому числу довжин хвиль , то в точці С спостерігається підсилення світла (максимум), а якщо , то відповідно послаблення (мінімум). Зрозуміло, що геометричним місцем точок, для яких виконується умова максимуму чи мінімуму, буде коло, тому, дивлячись зверху, ми побачимо темні та світлі кільця. Радіус деякого кільця на рис. 2 дорівнює r.

Оптична різниця шляху світлових променів утворюється у повітряному проміжку ВС. Позначимо його товщину d. Другий промінь проходить повітряний проміжок двічі, тому оптична різниця шляху дорівнює . Доданок виникає внаслідок того, що другий промінь відбивається від оптично більш густого середовища при цьому його фаза змінюється на протилежну. Прирівнюючи умову мінімуму (темні кільця) та оптичну різницю шляху , отримаємо, що товщина повітряного зазору для темних кілець повинна бути .

Запишемо теорему Піфагора для трикутника ОАВ (рис. 2), в якому катет ОА дорівнює R-d

, .

Величиною можна знехтувати тому що вона дуже мала в порівнянні з іншими величинами. Тоді , а підставляючи вираз для товщини повітряного проміжку , маємо

.

(1)

Радіус кривизни лінзи тоді дорівнює

Звичайно радіуси кілець вимірюють у поділках окулярної шкали. Для переводу цих значень у систему СІ величину радіуса кільця треба помножити на ціну поділки окулярної шкали a. Тоді остання формула для визначення радіуса кривизни лінзи набуває вигляду

(2)

Д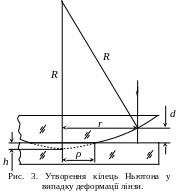 ля стабільності інтерференційної картини лінзу притискують до скляної пластинки. У цьому випадку лінза деформується, як показано на рис. 3, і формула (1) дає неправильні результати. Дивлячись у мікроскоп, тепер ми побачимо у центрі не точку, а темний круг радіус якого ρ. Величина деформації лінзи показана пунктиром і позначена літерою h.

Запишемо теорему Піфагора для прямокутного трикутника на рис. 3.

,

.

Величиною можна знехтувати тому що вона дуже мала в порівнянні з іншими величинами. Тоді .

Підставляючи товщину повітря-ного зазору , отримаємо

,

або

(3)

Порівняння формул (1) і (3) приводить до висновку, що залежність квадратів радіусів кілець від їх порядкового номера має лінійний характер. Коли деформація лінзи відсутня, то пряма проходить через початок координат, якщо ж лінза помітно деформована, то ця пряма не проходитиме через початок координат.

Для знаходження радіуса кривизни у випадку деформованої лінзи запишемо останню формулу для двох кілець із номерами m та n

,

і знайдемо різницю квадратів радіусів кілець

Звідси радіус кривизни лінзи дорівнює

або

Помножуючи радіуси кілець на ціну поділки окулярної шкали, маємо

(4)

Формула (4) дає можливість знаходити радіус кривизни у випадку деформації лінзи, але треба вимірювати радіуси двох кілець Ньютона.

Слід зазначити, що для світлих кілець треба використовувати умову максимуму . Нумерація темних кілець починається з нуля (темна центральна точка або круг має нульовий номер, перше темне кільце має перший номер, друге кільце – другій і так далі). Нумерація світлих кілець починається з одиниці.