Нелінійні явища, які виникають при взаємодії електричного поля хвилі з речовиною

1. Нелінійні діелектрики.

З курсу електрики відомо, що діелектрик, внесений в електричне поле, поляризується. Існує три види поляризації:

1. Електронна поляризація, або поляризація зміщення;

1. Іонна поляризація;

2. Орієнтаційна поляризація.

Поляризація діелектрика характеризується вектором поляризації Р. Вектор поляризації – це електричний момент одиниці об’єму поляризованого діелектрика. Практично всі рідкі діелектрики, а також більшість твердих діелектриків мають лінійну залежність між Р і Е, а саме для всіх видів поляризації

Р=а^.E

де Р – числове значення вектора поляризації, Е – напруженість електричного поля; а – макроскопічна лінійна електрична сприйнятливість (або поляризованість).

Зрозуміло, що а=αN де α – лінійна атомна сприйнятливість, N – кількість атомів в 1 см³, тоді зрозуміло, що

Р=αNE 6.1

Діелектрична проникність =1+4πа, а показник заломлення

n=

При дії потужних світлових потоків, потужність яких знаходиться в межах 10⁸-10¹⁰ Вт/см², поляризація діелектриків визначається нелінійним співвідношенням

P=aE+bE²+cE³, 6.2

у якому коефіцієнти b і с характеризують макроскопічну поляризованість другого й третього порядків. На рис. 6.1 показаний характер залежності поляризації Р від Е для трьох типів діелектриків: лінійного (b = с = 0), квадратичного (c = 0) і кубічного (b =0).

Якщо квадратичний діелектрик перебуває в електричному полі електромагнітної хвилі

_6.3

наприклад у хвилеводі, він піддається поляризації, залежність якої від часу значно відрізняється від синусоїдальної (рис. 6.2). Як видно з рисунка, поляризацію Р(t) кристала можна розкласти на три складові: 1) поляризацію, що змінюється залежно від основної частоти ; 2) поляризацію, яка змінюється залежно від подвоєної частоти 2 або другу гармоніку і 3) постійну поляризацію. З виразу (2) видно, що якщо прийняти c=0 і використати співвідношення (3), то

.

Оскільки ,

, 6.4

звідки випливає, що нелінійні оптичні явища зумовлені другим і третім членами. Другий доданок зумовлений виникненням змінної поляризації з частотою 2 . Третій доданок не залежить від часу і виражає статичну постійну поляризацію, зумовлену дією потужної світлової хвилі.

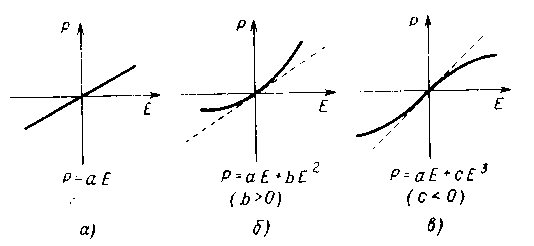
Рис. 6.1. Характеристики Р = f(Е) трьох типів діелектриків:

а — лінійного; b — квадратичного і в – кубічного

Рис. 6.2. Характеристики квадратичного нелінійного діелектрика:

вхідний сигнал Е = Е₀ соs t дає на виході поляризацію, яку

можна розкласти на три складові: основну (із частотою ),

другу гармоніку (із частотою 2 ) і постійну (статичну).

У цьому рівнянні ми знаходимо всі три складові поляризації, представлені на рис. 6.2 праворуч, а саме

_{P=P +P}² _+P⁰ _6.5

де

^6.6

є складовою основної поляризації, або першої гармоніки,

_6.7

— складовою другої гармоніки й

_6.8

— складова постійної (статичної) поляризації, що виникає винятково в змінному полі

Якщо в цьому полі перебуває кубічне середовище, то, як неважко довести, користуючись виразом cos³ t= (cos3 t+3cos t) сумарна поляризація буде складатися із двох складових — основної й третьої гармонік:

6.9

де

_6.10

6.11

2. Вплив електричного поля на та п. Позначимо зміну діелектричної проникності під впливом прикладеного зовнішнього електричного поля через

_.

Аналогічну зміну показника заломлення позначимо через

.

З теорії випливає, що і зміна діелектричної проникності, і зміна показника заломлення пропорційні квадрату прикладеного поля.

З великим ступенем наближення можливо записати, що

n_E=n+AE² 6.12

де А – коефіцієнт, що залежить від констант С і та інших.

Нелінійна залежність показника заломлення від напруженості поля призвела до відкриття нового дуже цікавого явища – самофокусування світла, коли світловий пучок у середовищі не розширюється, а навпаки, фокусується в тонкий світловий канал.

Але є й інші причини зміни показника заломлення в електричному полі. У нелінійному середовищі через електрострикцію світлова хвиля викликає появу постійного тиску. Це призводить до зміни густини і показника заломлення середовища. У рідинах з анізотропними молекулами показник заломлення змінюється через високочастотний ефект Керра. Показник заломлення завжди змінюється через нагрівання середовища світловою хвилею. У всіх цих випадках зміна показника заломлення пропорційна квадрату амплітуди (E²).

Коефіцієнт А може бути і додатнім, і від’ємним. Особливо велике значення він має для нітробензолу, при цьому знак його додатній.

Тому, якщо через однорідне середовище проходить інтенсивний пучок світла, то середовище стає оптично неоднорідне. Світловий промінь у такому середовищі відхиляється в бік більшого показника заломлення. З цим і пов’язане явище самофокусування (коли А > 0) і дефокусування (коли А < 0) світла, передбачене теоретично Г.А.Аскар’яном у 1962 році. Вперше спостерігали це явище М.Ф.Пилипецький і А.Р.Рустамов у 1965 році. Потім самофокусування спостерігалось для багатьох газів, рідин і твердих тіл.

Оскільки обмежений світловий пучок має більшу інтенсивність уздовж його осі, то показник заломлення в нелінійному середовищі (А > 0) більший на осі й зменшується у разі віддалення від неї до периферії. Внаслідок цього швидкість хвилі на периферії буде більша, ніж на осі, що приводить до зміни форми хвильового фронту, тобто відбувається самофокусування пучка. Для нелінійних середовищ (А<0) відбувається розфукусування. У деяких нелінійних середовищах пучок світла проходить без змін поперечних розмірів. Такий режим поширення світла називається самоканалізацією світлового пучка.

Підрахувавши величину критичної потужності (для ), одержимо . Таку і навіть більшу потужність можна одержати від рубінового лазера. В деяких сортах оптичного скла . В них явище самофокусування можна спостерігати не лише в інтенсивних пучках імпульсних лазерів, а й у мало інтенсивних пучках лазерів неперервної дії.