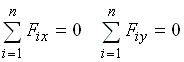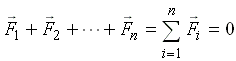СТАТИКА

1. Аксиомы статики

Аксиома 1. Две силы, действующие на абсолютно твердое тело уравновешива-ются только тогда, когда они равны по величине и направлены по од-ной прямой в противоположные стороны (рис. 1.2).

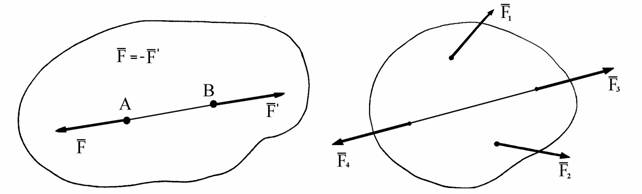
Рис. 1.2 Рис. 1.3

Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изме-нится, если прибавить к ней или отнять от нее уравновешенную сис-тему сил (рис. 1.3).

Следствие из аксиомы 1 и 2. Действие силы на абсолютно твердое тело (АТТ) не изменится, если точку приложения этой силы перенести по ли-нии ее действия. Пусть на тело в точке А действует сила (рис. 1.4). Добавим в точке В, выбранной произвольно на линии действия си-лы , уравновешенную систему сил и равных по абсолютной величине и направленных по линии ее действия. На основании аксиомы 1 силы и будут уравновешены и их можно отбросить (аксиома 2). В результате получим силу = , но приложенную не в точке А, а в точке В. Отсюда следует, что сила, приложенная к АТТ, есть вектор скользящий.

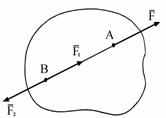
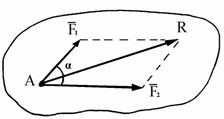
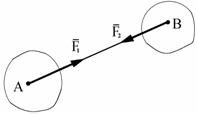
Рис. 1.4 Рис. 1.5 Рис. 1.6

Аксиома 3 Равнодействующая двух сил, приложенных к АТТ в одной точке, равна

их геометрической сумме , т.е. выражается по моду-лю и направлению диагональю

параллелограмма,построенного на этих силах (рис. 1.5).

Аксиома 4 Всякому действию одного тела на другое соответствует равное по величине,

но противоположное по направлению противодействие. Действие и противодействие-это силы,

приложенные к двум раз-личным телам, поэтому они не уравновешиваются (рис. 1.6).

Аксиома 5 Если деформируемое тело под действием системы сил находится в

равновесии, то при отвердевании его равновесие сохраняется.

Под действием сил тело D находится в равновесии. Если трос CB заменить стержнем,

то равновесие не нарушится, равновесие не нарушится и в том случае, если трос BD

за-менить стержнем, если же стержень АВ заменить тросом - равновесие нарушится

(рис. 1.7).

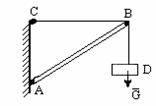
Рис.1.7

2. Связи и их реакции

3. Системы сходящихся сил. Теорема о существовании равнодействующей. Условия равновесия.

Система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.

Пусть система сходящихся сил (F₁, F₂,...,F_n) приложена к твердому телу (рис. 12, a).

Согласно следствию второй аксиомы, п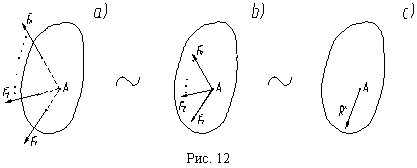 ереносим все силы системы в точку пересечения линий действия A и получаем систему сил, приложенных в одной точке (рис. 12, b). По аксиоме параллелограмма сил, начиная с сил F₁ и F₂, последовательно складываем силы, добавляя каждый раз к полученной сумме по одной силе системы. Дойдя до последней силы F_n, выясняем, что система сил (рис. 12, b) эквивалентна одной силе или равнодействующей R^* (рис. 12, c), равной геометрической сумме сил системы.

Таким образом, система сходящихся сил приводится к равнодействующей (эквивалентна равнодействующей), которая равна геометрической сумме сил системы и приложена в точке пересечения линий действия сил:

(F1, F2,...,Fn) ~ R*; R* = F1 + F2 + ... + Fn

Для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы геометрическая сумма всех сил системы была равна нулю:

для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник системы был замкнутым.

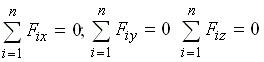
Для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил системы на оси координат были равны нулю.