3. Первый признак сравнения рядов.

Пусть и - два знакоположительных числовых ряда и выполняется неравенство для всех k = 1, 2, 3, ... Тогда из сходимости ряда следует сходимость , а из расходимости ряда следует расходимость .

Второй признак сравнения.

Пусть и - знакоположительные числовые ряды. Если , то из сходимости ряда следует сходимость . Если , то из расходимости числового ряда следует расходимость .

Признак Даламбера. Если предел отношения последующего члена ряда ( 1 ) к предыдущему меньше 1 , то ряд сходится, если больше 1, то ряд расходится

Если , то при l < 1 сход., при l > 1 расход., при l = 1 – сомнительный случай

Док-во. Отношения (u_{n + 1} / u_n ) образуют вспомогательную числовую последовательность, которая может сходится или расходится. Необходимое условие сходимости : Для всякого  > 0 существует такое N , что при n > N выполняется неравенство l -  < u_{n + 1} / u_n < l +  , т.е. с ростом n член последовательности оказывается в сколь угодно малой  - окрестности точки l .

Пусть l < 1,  мало и q = l +  < 1 , тогда из условия u_{N + 1} / u_N < q следует u_N+1 <qu_N, u_N+2 <q u_N+1 < q²u_N , u_N+3 < q³u_N , . . . В результате получаем две числовые последовательности : u_{N ,} u_N+1 , u_N+2 , . . . и u_N , q u_N , q² u_N, q³ u_N . . . связанные неравенством u_N+n < u_N qⁿ. Строим из них ряды. Т.к. ряд с большими членами (геометрическая прогрессия, q < 1) сходится, то ряд с меньшими членами также сходится по признаку сравнения и по свойству 1⁰ сходится исходный ряд . При l > 1 аналогичным образом получаем обратный результат.

Интегральный признак Коши. Cумма членов бесконечной числовой последовательности u_n = f(n) сходится, если сходится несобственный интеграл 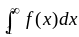и расходится при расходимости интеграла.

Д ок-во. Ряд f(1) + f(2) + f(3) + . . . можно понимать как площадь ступенчатой фигуры, построенной вдоль кривой y=f(x), а интеграл как площадь криволинейной трапеции y = f(x) Если площадь криволинейной трапеции ограничена, то и площадь ступенчатой фигуры будет ограничена, и сумма ряда будет иметь конечное значение.

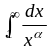Пр. Обобщенный гармонический ряд . Вычислим интеграл J = При  = 1 J = ln x |₁^ =  , при   1 J = x^{1 - } /(1-) |₁^ Отсюда следует, что при  > 1 обобщенный гармонический ряд сходится, а при  1 расходится.

4. Знакочередующиеся числовые ряды.

Опр. Знакочередующимся наз. числовой ряд вида , u_n > 0 ( 3 )

Признак Лейбница. Если члены ряда ( 3 ) последовательно убывают ( u_n > u_n+1 ) и стремятся к 0 ( lim u_n = 0 при n   ), то ряд сходится, причем, его сумма S > 0 и S < u₁.

Док-во. Члены частичной суммы S_2m сгруппируем двумя способами :

S_2m = (u₁ – u₂) + (u₃ – u₄) + . . . +(u_2m-1 – u_2m) ( a )

S_2m = u₁ – (u₂ – u₃) – (u₄ – u₅) - . . . – (u_2m-2 – u_2m-1) – u_2m ( b )

При способе ( а ) имеем сумму положительных членов S_2m > 0. При способе (b) имеем разность между u₁ и суммой (m – 1) положительного слагаемого. Из этого следует, что S_2m всегда ограничена S_2m < u₁ , а последовательность ограниченных S_2m имеет предел, т.е. ряд сходится. От S_2m+1 легко перейти к S_2m , выделив лишний член.

Знакопеременные числовые ряды.

Опр. Знакопеременным наз. числовой ряд составленный из положительных и отрицательных членов.

Признак абсолютной сходимости. Если ряд, составленный из модулей элементов знакопеременного ряда, сходится, то и сам знакопеременный ряд является сходящимся ,

т.е. из сходимости ряда (a) следует сходимость ряда (b)

Док-во. В частичной сумме ряда (b) S_n выделим все положительные слагаемые S_n’ и отрицательные слагаемые S_n’’. Тогда имеем для (b) : S_n = S_n’ - S_n’’ и для (а) :

_n = S_n’ + S_n’’ ,следовательно, S_n < _n . Из условия сходимости ряда (а) следует _n <  или S_n < _n <  , т.е. частичные суммы S_n ограничены и, следовательно, знакопеременный ряд (b) сходится.

Признак абсолютной сходимости является достаточным, но не необходимым.

Пр. Ряд сходится по признаку Лейбница ( u_n = 1/n > u_n+1 = 1/(n+1) - да,

lim u_n = lim 1/n = 0 - да ), а гармонический ряд является расходящимся.

Опр. Сходящийся знакопеременный ряд наз. абсолютно сходящимся, если также сходится ряд составленный из модулей его членов, и условно сходящимся, если ряд из модулей не сходится.

На абсолютно сходящиеся ряды переносятся все основные свойства конечных сумм.

5. Функциональный ряд.

Опр. Функциональным наз. ряд члены которого являются функциями от х .

= u₁(x) + u₂(x) + u₃(x) + . . . = S(x)

При фиксированном x = a функциональный ряд становится числовым.

Опр. Областью сходимости функционального ряда наз. множество всех значений х при которых он сходится. В области сходимости сумма ряда S(x) является функцией от х.

Пр. т.к. члены ряда положительны применим признак Даламбера

lim u_n+1 / u_n = e^-x < 1 при х (0,  ), т.е. ряд в этом интервале сходится.

Степенной ряд.

Опр. Степенным наз. функциональный ряд вида

= a₀ + a₁(x – x₀) + a₂(x – x₀)² + . . . ( 5 )

где х₀ и коэффициенты ряда а_n  R . При х₀ = 0 получаем ряд по степеням х

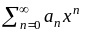= a₀ + a₁x + a₂x² + a₃x³ + . . . ( 6 )

Теорема Абеля Если степенной ряд ( 6 ) сходится при х = х₁, то он абсолютно сходится при всех значениях х меньших х₁ по модулю ( |x| < |x₁| ). Если ряд ( 6 ) расходится при х = х₂ , то он расходится при всех значениях х больших х₂ по модулю ( |x| > |x₂| ).

Док-во. Пусть при х = х₁ ряд ( 6 ) сходится, т.е. и все его члены ограничены a_nxⁿ < M. Преобразуем ( 6 ) к виду ( 7 )

Введем в ряд (7) модули ( 8 )

и сравним его с рядом ( 9 )

Большими оказываются члены ряда ( 9 ) : |a_n x₁ⁿ| (|x/x₁|)ⁿ < M (|x/x₁|)ⁿ , который является геометрической прогрессией. При |x| < |x₁| ряд ( 9 ) сходится, следовательно, сходится и ряд с меньшими членами ( 8 ) и абсолютно сходятся ряды ( 7 ) и ( 6 )

Пусть при х = х₂ ряд ( 6 ) расходится. Предположим, что существует х большее х₂ по модулю (|x| > |x₂|), при котором ряд ( 6 ) сходится. Но тогда он должен сходится и при x₂. Это противоречие исключает предположение о сходимости ряда при |x| > |x₂| .

6. Ряды Тейлора и Маклорена.

Имеем степенной ряд, сходящийся на интервале (x₀ – R, x₀ + R). Суммой ряда является функция f(x)

= f(x)

Покажем, что коэффициенты этого ряда связаны простым соотношением с f(x) .

Будем последовательно дифференцировать обе части равенства ( 11 ) и вычислять производные при х = х₀

f (x) = a₀ + a₁(x – x₀) + a₂(x – x₀)² + a₃(x – x₀)³ + … + a_n(x – x₀)ⁿ + . . . , f(x₀) = a ₀

f ‘(x) = a₁ + a₂(x – x₀) + a₃(x – x₀)² + … + n a_n(x – x₀)^n-1 + . . . , f ‘(x₀) = a₁

f ‘’(x) = a₂ + a₃(x – x₀) + a₄(x – x₀)² + … + n(n – 1) a_n(x – x₀)^n-2 + . . . , f ‘)’(x₀) = 2 a₂

f ‘’’(x) = a₃ + a₄(x – x₀) + a₅(x – x₀)² +…+ n(n–1)(n–2)a_n(x – x₀)^n-3 + . . . , f’’’(x₀) = 23 a₃

f⁽ⁿ⁾ (x) = n(n–1)(n–2) . . . 2 1 a_n + . . . , f ^{( n )}(x₀) = n ! a _n

Отсюда находим коэффициенты a₀ = f(x₀) , a_n = f ^{( n )}(x₀) / n ! ( 12 )

Таким образом, если бесконечно дифференцируемая в точке х₀ функция f(x) разлагается в степенной ряд, то этот ряд имеет вид

f(x) = и наз. рядом Тейлора , а при х₀ = 0 наз. рядом Маклорена.