Исследование влияния количества аппроксимирующих прямых на точность аппроксимации.
Уберем точку (122;116), чтобы исследовать влияние количества аппроксимирующих прямых на точность аппроксимации. Получим 8 аппроксимирующих прямых.
Расчет для новой аппроксимирующей прямой:
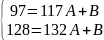
Вычтем из уравнения 97=117A+B уравнение 128=132A+B и получим -31=-15A, откуда находим A=2.067.
Подставим A в уравнение: 97=117*2.067+B. Получим B=-144.839
Уравнение новой прямой: Q=2.067*V-144.839
Проверка
правильности расчета коэффициентов:
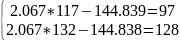совпадает со значениями из таблицы.
Расчет погрешности для новой аппроксимирующей прямой:
Подставим V=117 в уравнение Q=2.067*V-144.839
Q=2,067*117-144.839=97;
Qтаб.=97;
Qmax=134;
Qmin=76;
Подставим полученные значения в формулу:
Получим:
Подставим V=122 в уравнение Q=2.067*V-144.839
Q=2.067*122-144.839=107.335;
Qтаб.=116;
Qmax=134;
Qmin=76;
Подставим полученные значения в формулу:
Получим:
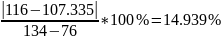
Подставим V=132 в уравнение Q=2.067*V-144.839
Q=2.067*132-144.839=128.005;
Qтаб.=128;
Qmax=134;
Qmin=76;
Подставим полученные значения в формулу:
Получим:
Расчет суммарной погрешности:
Qsumн=1.7%+3.4%+0.862%+14.939%+0.008%=20.909%
ОПИСАНИЕ АЛГОРИТМОВ
Описание алгоритма 1
Для расчета значения функции Q необходимо составить разветвляющийся алгоритм. Решением для этого алгоритма является 8 блок-схем условного перехода. В зависимости от того, какое значение примет аргумент V, будет зависеть, по какому уравнению будет рассчитано значение функции Q.
Описание алгоритма 2
Для расчета всех значений функции Q необходимо составить циклический алгоритм с разветвлением. Решением для этого алгоритма является итерационные циклы с предусловием. Выход из цикла осуществляется по достижению аргумента V максимального значение равного 140. Состоит этот алгоритм из 8 блок-схем условного перехода и в зависимости от того, какое значение примет аргумент V, будет зависеть, по какому уравнению будет рассчитано значение функции Q. Для каждой итерации на экран монитора будет выведено полученное значение функции Q и текущее значение аргумента V. Увеличение аргумента V происходит в 4 этапа по разным шагам: при V от 90 до 102 увеличение происходит на 4; при V от 102 до 117-на 5; при V от 117 до 122- на 10; при V от 132 до 140 на 8.
Описание алгоритма 3
Для нахождения всех значений функции Q, нахождения максимального и минимального значения функции Q, минимального и максимального значения необходимо составить алгоритм с разветвлением и циклами поиска минимальных и максимальных значений.
Решением для этого алгоритма является цикл нахождения минимальной и максимальной погрешности, а так же нахождение максимального и минимального значений функции Q. Нахождение значений функции Q осуществляется при помощи итерационного цикла с постусловием. Выход из цикла осуществляется по достижению аргумента V максимального значение равного 140. В теле цикла находится 8 блок-схем условного перехода и в зависимости от того, какое значение примет аргумент V, будет зависеть, по какому уравнению будет рассчитано значение функции Q. После каждой итерации будет происходить увеличение аргумента V на шаг и запись полученного значения функции Q в массив PQ, где PQ – массив в котором хранятся рассчитанные значения функции Q.
Для нахождения максимального и минимального значений массива PQ, первому элементу массива присваивается максимальное (max) и минимальное (min) значения. Затем организуется цикл со счетчиком, в теле которого находится условие, состоящее из двух блок-схем условного перехода. Если текущий элемент меньше минимального, то текущему элементу присваивается минимальное значение. Если текущий элемент больше минимального, то текущий элемент сравнивается с максимальным. Если текущий элемент больше максимального, то текущему элементу присваивается максимальное значение, в противном случае начинается новая итерация
Для нахождения максимальной и минимальной погрешности необходимо найти ΔQ, где ΔQ – разность между максимальным и минимальным табличными значениями функции Q.
Для того чтобы найти ΔQ, нужно при помощи цикла записать все табличные значения функции Q в массив TQ. После чего найти минимальный и максимальный элемент массива TQ. Для нахождения максимального и минимального значений массива TQ, первому элементу массива присваивается максимальное (max) и минимальное (min) значения. Затем организуется цикл со счетчиком, в теле которого находится условие, состоящее из двух блок-схем условного перехода. Если текущий элемент меньше минимального, то текущему элементу присваивается минимальное значение. Если текущий элемент больше минимального, то текущий элемент сравнивается с максимальным. Если текущий элемент
больше максимального, то текущему элементу присваивается максимальное значение, в противном случае начинается новая итерация.
После нахождения максимального и минимального значений массива TQ, необходимо вычесть из максимального элемента минимальный. После нахождения ΔQ, необходимо вычислить погрешности для всех точек функции.
Для этого в массиве проводим расчет по формуле:
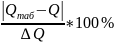
где,
табличное значение функции в данной точке
рассчитанное значение функции
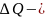разность
между максимальным и минимальным
табличными значениями функции Q
И записываем все полученные значения в массив ERR.
Для нахождения максимального и минимального значений массива ERR, первому элементу массива присваивается максимальное (max) и минимальное (min) значения. Затем организуется цикл со счетчиком, в теле которого находится условие, состоящее из двух блок-схем условного перехода. Если текущий элемент меньше минимального, то текущему элементу присваивается минимальное значение. Если текущий элемент больше минимального, то текущий элемент сравнивается с максимальным. Если текущий элемент больше максимального, то текущему элементу присваивается максимальное значение, в противном случае начинается новая итерация.
После завершения цикла, на экран выводится максимальное и минимальное значения массива PQ и максимальное и минимальное значения массива ERR.