Этап 1.

1. Полагаем t=. Тогда функция будет иметь вид:

Все данные задачи заносим в жорданову таблицу. В строке f_ этой таблицы в каждый столбец записываем число, равное сумме чисел c_j и d_j. Кроме того, добавим в таблицу две строки для записи функций f_t с произвольным параметром t. При этом в предпоследней строке записываем коэффициенты c j , а в последней –d j . Чтобы получить

f t , нужно умножить коэффициенты последней строки на t и сложить их с коэффициентами предпоследней.

таблица 1

2. Находим оптимальный план задачи обычным симплекс-методом, подвергая преобразованию и элементы последних двух строк.

Предположим, что план, представленный в таблице 1, является оптимальным. Тогда все коэффициенты f_ -строки неотрицательны:

таблица 2

Поскольку оптимальный план найден, переходим к выполнению действий этапа II.

Этап 2.

1. Находим значения параметра t , при которых план в таблице 2 будет оставаться оптимальным (максимум f t достигается в той же вершине). Для этого необходимо, чтобы все коэффициенты функции f t были неотрицательны:

Из этой системы видно, что во всех случаях, кроме q j 0(при q j неравенство p j q_j t выполняется при любых значениях t ; следовательно, на столбец, в котором находится q j , можно не обращать внимания), границей изменения параметра t служит отношение . Поэтому просматриваем элементы q_j последней строки таблицы: если все онибольше нуля, переходим к п. 2; если все они меньше нуля, – к п. 3; если жесреди элементов j q имеются и положительные, и отрицательные, – к п. 4.

2. Пусть все q j . Среди отношений выбираем наибольшее.

Таким образом,

В интервале [₁;₂) функция достигает максимума в той же вершине, что и при t=, следовательно, t[₁;₂)

3. Пусть все q_j . Среди отношений выбираем наименьшее. Если взять 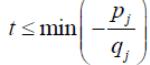, то все условия будут удовлетворены. Нижней границы для t в этом случае не существует, поэтому его можно уменьшать бесконечно. Значит,

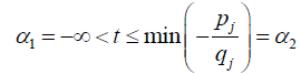
Как и прежде, t[₁;₂).

4. Пусть среди элементов q_j имеются как положительные, так и отрицательные. Разделим систему неравенств на две подсистемы соответственно знакам коэффициентов q_j . Тогда из подсистемы неравенств с q_j > 0 получим , а из второй подсистемы q_j < 0 будем иметь 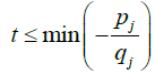Следовательно, вся система неравенств будет удовлетворяться, если t будет принимать значения:

В этом случае выделенный интервал, в котором функция достигает максимума в той же вершине, что и при t=, является отрезком, t[₁;₂].

5. Сравниваем полученный интервал [₁;₂] с заданным [;].Независимо от значения 1 левой границей первого интервала будет , так как ₁ больше быть не может. Если _то весь интервал ;попадает внутрь интервала __и задача решена. Для любого значения параметра t;максимум функции f_t достигается в одной и той же вершине

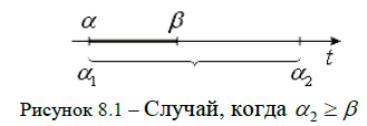
6. Если _, то в интервале _максимум функции ft будет в найденной вершине (рисунок 8.2). Исключаем этот интервал из рассмотрения и решаем задачу для оставшегося интервала 2;. Для этого придаем t значение _и заменяем строку fстрокой f. В результате замены получаем новую таблицу

За разрешающий столбец в новой таблице примем тот, по которому определено значение t=₂ (в этом столбце на пересечении с f_2 -строкой находится элемент, равный нулю). Если нули находятся в нескольких столбцах, то в качестве разрешающего можно брать любой из них.

Разрешающий элемент находим по наименьшему симплексному отношению и делаем один шаг модифицированных жордановых исключений. Получаем следующее по порядку оптимальное решение, так как все коэффициенты в строке f_2 при преобразовании не изменятся.

Для найденного решения снова определяем интервал изменения параметра t, для чего переходим к п. 1.

Если в разрешающем столбце не окажется положительных коэффициентов, то функция f_t при t>₂ не ограничена; задача на оставшемся интервале 2; решения не имеет.

Замечание. При отыскании оптимального решения для t= (при выполнении п. 2 этапа I алгоритма) может оказаться, что функция f_ сверху не ограничена. В этом случае в разрешающем столбце j₀ коэффициент f_- строки отрицателен , а все остальные коэффициенты столбца j₀ неположительны.

При значениях t> на пересечении строки f_t и столбца j₀ будет элемент . Нас интересуют значения этого элемента, так как они определяют поведение функции при . Выберем такое значение t=t₀, при котором коэффициент . Отсюда получаем .

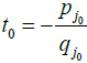Если значение элемента , то для всех коэф-т разрешающего столбца в строке f_t будет отрицательным . Следовательно, на всем заданном отрезке целевая функция f_t не ограничена (задача решения не имеет).

Если элемент , то при коэф-т, находящийся в разрешающем столбце и f_t-строке, будет отрицательным. Значит и в этом случае целевая функция не ограничена и задача решения не имеет.

При значении t=t₀ коэф-т , а при дальнейшем увеличении t, он будет положительным. К отрезку применяем последовательно алгоритм решения задачи.