В14 Модели межотраслевого баланса. Продуктивность балансовой модели

Рассмотрим вопрос, который не был изучен в предыдущем параграфе, касающийся существования матрицы Определение 16.1. Если все элементы матрицы A (вектора B) неотрицательны, то матрицу A (вектор B ) будем называть неотрицательной (неотрицательным) и обозначать этот факт так: . Вектор B назовем положительным, если все его координаты положительны. Заметим, что в модели межотраслевого баланса матрица A прямых производственных затрат по своему экономическому смыслу может быть только неотрицательной. Определение 16.2. Неотрицательную матрицу A назовем продуктив-ной, если для любого неотрицательного вектора Y найдется неотрицательный вектор X, для которого справедливо равенство Для модели межотраслевого баланса с матрицей A прямых производственных затрат это означает, что любой неотрицательный конечный спрос может быть удовлетворен (т.е. для него найдется соответствующий план валового выпуска). Следующая теорема показывает, что продуктивность матрицы A непосредственно связана с обратимостью матрицы (E-A). Теорема 16.1. (критерий продуктивности) Неотрицательная матрица A продуктивна тогда и только тогда, когда матрица (E-A) обратима, причем обратная матрица неотрицательна. Следствие 16.1. Если матрица A продуктивна, то система неравенств имеет только неотрицательные решения. Следующая теорема играет важную роль в математической экономике. В частности, она оказывается полезной и при исследовании продуктивности матриц. Теорема 16.2 (Фробениус, Перрон) Пусть A – произвольная неотрицательная матрица. Тогда существует собственное значение матрицы A, такое, что для всех собственных значений матрицы A выполняется неравенство . Кроме того, существует неотрицательный собственный вектор матрицы A, соответствующий значению . Замечание 16.1. Известно, что набор собственных значений у матриц A и одинаков, к тому же условие равносильно условию . Следовательно, . Соответствующий вектор обозначим через . Определение 16.3. Число называется числом Фробениуса матрицы A. Векторы называются, соответственно, правым и левым векто-ром Фробениуса матрицы A. Понятие числа Фробениуса позволяет кратко сформулировать условие продуктивности матрицы МОБ. Теорема 16.3. Модель Леонтьева с матрицей A продуктивна тогда и только тогда, когда . Необходимость. Пусть матрица A продуктивна и ее правый и левый векторы Фробениуса равны, соответственно, . По критерию продуктивности у системы уравнений существует неотрицательное решение Тогда 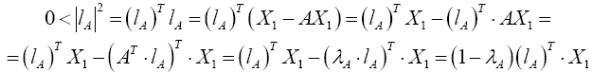Векторы неотрицательны, поэтому .Следовательно, Достаточность. Если , то для всех собственных значений  матрицы A справедливо неравенство . Данная теорема сводит проверку продуктивности матрицы к нахождению ее числа Фробениуса, т.е. наибольшего по модулю собственного значения. Следствие 16.2. Если у положительной матрицы сумма по каждому столбцу меньше единицы, то эта матрица – продуктивная.