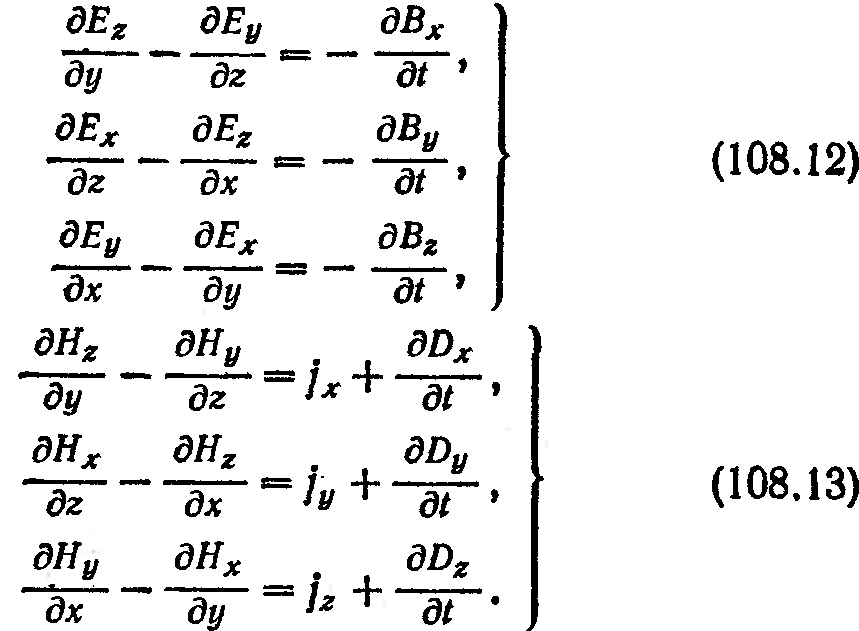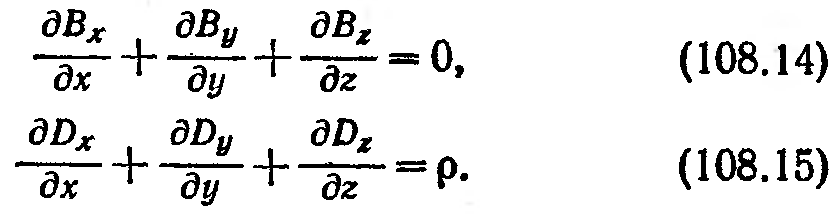Плоская электромагнитная волна

Рассматривая электромагнитные волны (ЭМВ), необходимо отдавать себе отчет в том, что, их природа отличается от природы волн механических. Например, ЭМВ состоят из двух компонент. Как следствие, структуру волн необходимо исследовать дополнительно.

Рассмотрим плоскую ЭМВ в однородной непроводящей среде (j = 0, D = ₀Е, В = ₀Н,  и  – постоянные). Тогда уравнения Максвелла примут вид:

Пусть ось распространения волны х перпендикулярна к волновым поверхностям. Тогда Е и Н, а, следовательно, и их составляющие, не будут зависеть от координат у и z. Поэтому уравнения (108.12) – (108.15) упрощаются следующим образом:

(110.1)

(110.2)

(110.3)

(110.4)

Первое из уравнений (110.2) и уравнение (110.4) показывают, что Е_х не может зависеть ни от t, ни от х. Первое из уравнений (110.1) и уравнение (110.3) дают тот же результат для Н_х. То есть Е_х и Н_х могут быть лишь постоянными однородными полями, наложенными на электромагнитное поле волны. В дальнейшем мы будем предполагать отсутствие постоянных полей: Е_х = Н_х = 0. Остальные уравнения показывают, что поле волны не имеет составляющих вдоль оси х, т. е. векторы Е и Н перпендикулярны к направлению распространения волны k – электромагнитные волны поперечны.

Два последних уравнения (110.1) и два последних уравнения (110.2) можно объединить в две независимые группы:

(110.5)

(110.6)

Первая группа уравнений связывает составляющие E_y и H_z, вторая E_z и Н_у.

Из структуры уравнений видно, что поле E_y создает магнитное поле H_z и наоборот. Ни поле E_z, ни поле Н_у при этом не возникают. Это означает, что для описания плоской электромагнитной волны достаточно взять одну из систем уравнений (110.5) или (110.6).

Возьмем для описания волны уравнения (110.5), положив E_z = Н_у = 0. Продифференцируем первое уравнение по х и произведем замену: . Подставив затем из второго уравнения, получим волновое уравнение для E_y:

(110.7)

После аналогичных преобразований получим волновое уравнение для H_z:

(110.8)

Напомним, что остальные составляющие Е и Н равны нулю, так что Е = Е_у и H = H_z. Индексы у и z при Е и Н сохранены в уравнениях (110.7) и (110.8) только чтобы подчеркнуть поперечность векторов Е и Н.

Уравнения (110.7) и (110.8) представляют собой частный случай уравнений (109.8) и (109.9). Простейшее решение уравнения (110.7) – гармоническая функция:

(110.9)

Решение уравнения (110.8) имеет аналогичный вид

(110.10)

В этих формулах  – частота волны, k – волновое число, равное /u, ₁ и ₂ – начальные фазы колебаний в точках с координатой х = 0.

Нетрудно показать, что начальные фазы колебаний векторов Е и Н равны. Подставим функции (110.9) и (110.10) в уравнения (110.5) :

Для выполнения полученных равенств необходимо:

равенство начальных фаз

₁ = ₂,

равенство амплитуд при гармонических функциях:

.

Перемножив эти два равенства, получим

Таким образом, колебания электрического и магнитного векторов в электромагнитной волне происходят с одинаковой фазой (₁ = ₂), а амплитуды этих векторов связаны соотношением

(110.11)

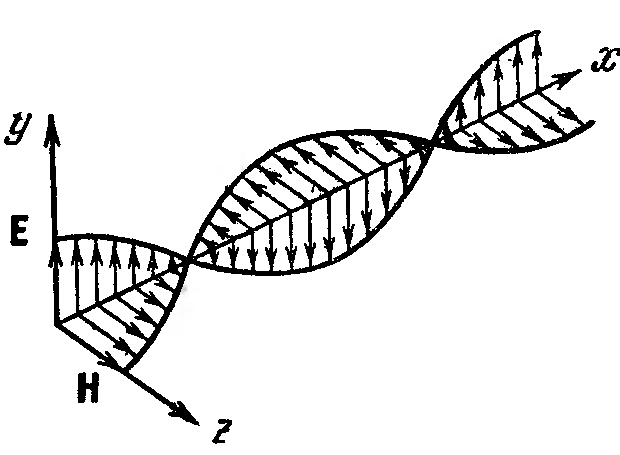
Теперь можно легко получить уравнение плоской волны в векторном виде. Умножим уравнение (110.9) на орт оси у (Е_у j = Е), а уравнение (110.10) на орт оси z (H_z k= H). Тогда:

(110.13)

(₁ =₂ = 0).

Рис. 237

Результат проведенного анализа представлен на рис. 237. Здесь приведена «моментальная фотография» плоской электромагнитной волны. Как видно из рисунка, векторы Е и Н образуют с направлением распространения волны правовинтовую систему: если Е направлен вверх, то Н направлен вправо. При рассмотрении смотрим вдоль направления, по которому распространяется волна. В фиксированной точке пространства векторы Е и Н изменяются со временем по гармоническому закону синфазно.