ВОЛНЫ

Распространение волн в упругой среде.

Процесс распространения колебаний в пространстве называется волной. Между частицами упругой (твердой, жидкой или газообразной) среды существуют взаимодействия. Поэтому при возбуждении колебания ее частиц в каком–либо месте это колебание начнет распространяться в среде от частицы к частице с некоторой скоростью u.

Частицы среды, в которой распространяется волна, не переносятся волной, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Механические поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.

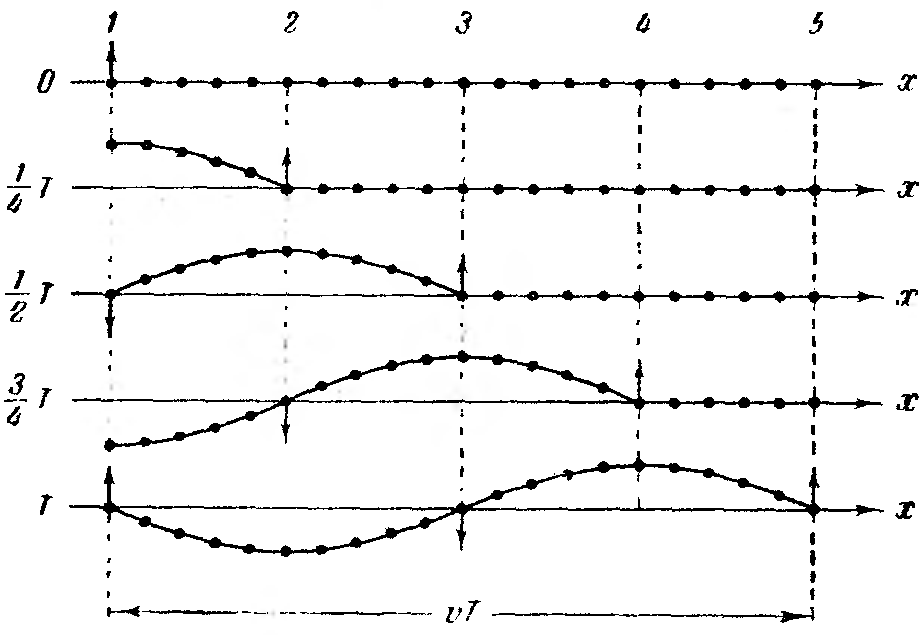
Рис. 192.

На рис. 192 показано движение частиц при распространении в среде поперечной волны. Номерами 1, 2, 3 и т. д. обозначены частицы, отстоящие друг от друга на расстоянии, равном ¼ uT, т. е. на расстоянии, проходимом волной за четверть периода колебаний, совершаемых частицами. В момент времени, принятый на схеме за нулевой, волна, распространяясь вдоль оси слева направо, достигла частицы 1, вследствие чего частица начала смешаться из положения равновесия вверх, увлекая за собой следующие частицы. Спустя четверть периода частица 1 достигает крайнего верхнего положения; одновременно начинает смещаться из положения равновесия частица 2. Спустя еще четверть периода первая частица будет проходить положение равновесия, двигаясь в направлении сверху вниз, вторая частица достигает крайнего верхнего положения, а третья частица начинает смещаться вверх из положения равновесия.

В момент времени, равный Т, первая частица закончит полный цикл колебания и будет находиться в таком же состоянии движения, как и в начальный момент. Волна к моменту времени Т, пройдя путь uT, достигнет частицы 5.

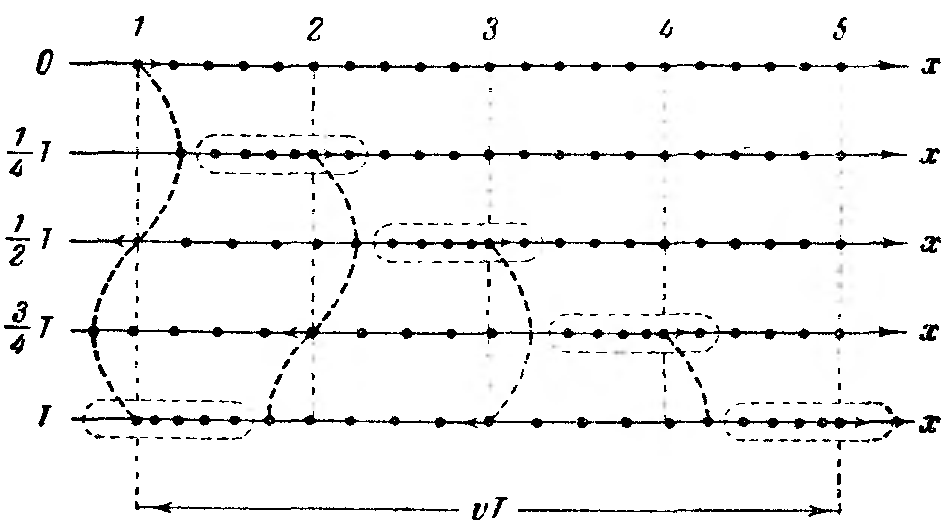
Рис. 193.

На рис. 193 показано движение частиц при распространении в среде продольной волны. Все рассуждения, касающиеся поведения частиц в поперечной волне, могут быть отнесены и к данному случаю с заменой смещений вверх и вниз смещениями вправо и влево. Как видно из рис. 193, при прохождении продольной волны в среде создаются чередующиеся сгущения и разрежения частиц (сгущения частиц отмечены на рисунке пунктиром), перемещающиеся в направлении распространения волны со скоростью u.

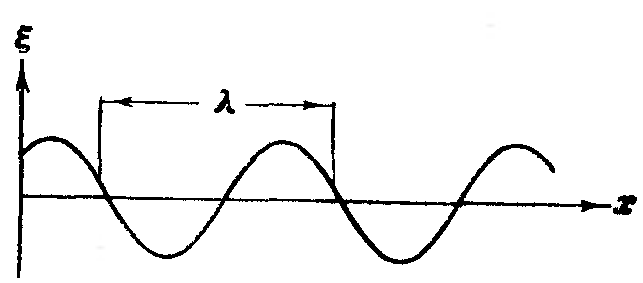
Как видно из рис. 192 и 193, частицы среды в различных её областях колеблются со сдвигом по фазе. Частицы, положения равновесия которых отстоят друг от друга на расстоянии uT, колеблются в одинаковой фазе. Расстояние между ближайшими частицами, колеблющимися одинаковым образом (в одинаковой фазе), называется длиной волны . В пределах пространства, заполненного колебаниями, распределение смещений частиц  из положения равновесия как функция расстояния х, отсчитываемого вдоль направления распространения волны, представлено на рисунке.

Рис. 194.

Длина волны, очевидно, равна тому расстоянию, на которое распространяется волна за период:

 = uT. (77.1)

Заменяя в этом соотношении Т через 1/v (v – частота колебаний), получим:

v = u (77.2)

В действительности колеблются не только частицы, расположенные вдоль оси х (как это изображено на рис. 192 и 193), а совокупность частиц, заключенных в некотором объеме. Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом). Фронт волны представляет собой поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Характерной особенностью волнового фронта является синфазность колебаний точек, образующих фронт.

Геометрическое место точек, колеблющихся в одинаковой фазе внутри области, занятой колебаниями, называется волновой поверхностью.

Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени только один. Волновые поверхности остаются неподвижными (они проходят через положения частиц, колеблющихся в одинаковой фазе). Волновой фронт все время перемещается.

Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой систему параллельных друг другу плоскостей, в сферической волне – систему концентрических сфер.

Уравнения плоской и сферической волн

Уравнением волны называется выражение, которое дает смещение колеблющейся точки, как функцию ее координат равновесного положения точки, х, у, z и времени t:

 = (х, у, z; t) (78.1)

Функция (78.1) должна быть периодической как относительно времени t, так и относительно координат х, у и z. Периодичность по t следует из того, что  описывает колебания точки с координатами х, у, z. Периодичность по координатам вытекает из того, что точки, отстоящие друг от друга на расстоянии , колеблются одинаковым образом.

Достаточно просто найти вид функции  можно в случае плоской волны в предположении гармонического характера колебаний. Пусть для простоты ось координат х совпадает с направлением распространения волны. Тогда волновые поверхности перпендикулярны к оси х и, поскольку все точки волновой поверхности колеблются одинаково, смещение  будет зависеть только от х и t:

 = (х, t)

Ещё одно упрощение: колебания точек, лежащих в плоскости х = 0 (рисунок), гармонические

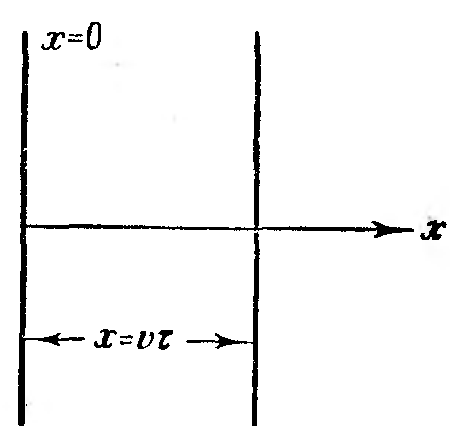
(0, t) = a cos t

Вопрос: каков вид колебания частиц в плоскости с произвольным значением х ?

Чтобы пройти путь от плоскости х = 0 до этой плоскости, волне требуется время

 = x/u

где u – скорость распространения волны. Следовательно, колебания частиц, лежащих в плоскости х, отстают по времени на  от колебаний частиц в плоскости х = 0. Тогда уравнение плоской волны запишется следующим образом:

(х, t) = a cos (t – ) = а cos (t – x/u) (78.2)

Величина  в (78.2) есть смещение любой из точек с координатой х в момент времени t. При выводе предполагалось, что энергия волны не поглощается средой. Как следствие, амплитуда колебаний плоской волны во всех точках одна и та же.

Если зафиксировать значение фазы, стоящей в уравнении (78.2):

 (t – x/u) = const (78.3)

можно путём дифференцирования получить скорость dx/dt, с которой перемещается данное значение фазы:

откуда

(78.4)

Скорость распространения волны u в уравнении (78.2) есть скорость перемещения фазы или фазовая скорость.

Из (78.4) следует, что скорость волны положительна. Следовательно, уравнение (78.2) описывает волну, распространяющуюся в сторону возрастания х. Тогда волна, распространяющаяся в противоположном направлении, имеет вид

 = а cos (t + x/u) (78.5)

Уравнению плоской волны можно придать симметричный относительно t и x вид. Для этого вводится так называемое волновое число k:

k = 2 / (78.6)

Получаются полезные соотношения:

(78.7)

с использованием которых уравнение плоской волны приобретает вид

 = а cos (t – kx) (78.8)

Уравнение волны, распространяющейся в сторону убывания х, отличается от (78.8) только знаком при члене kx.

Всякий реальный источник волн обладает некоторой протяженностью. Однако если расстояние от источника, значительно превышает его размеры, то источник можно считать точечным. В случае изотропной среды скорость распространения волны во всех направлениях одна и та же. Тогда порождаемая точечным источником волна будет сферической.

Пусть фаза колебаний источника равна  t. Чтобы пройти путь r, волне требуется время  = r/u Тогда фаза колебаний точки на волновой поверхности радиуса r равна (t – r/u).

При распространении сферической волны даже в отсутствии потерь энергии колебаний, амплитуда колебаний не постоянна. Это утверждение следует из закона сохранения энергии: полная энергия колебаний всех точек любой волновой поверхности должна быть равна энергии колебаний источника. Поэтому энергия колебаний каждой точки уменьшается при увеличении поверхности пропорционально величине поверхности: W_кол  1/r². Энергия колебаний каждой точки пропорциональна квадрату амплитуды колебаний W_кол  а². Отсюда следует: а  1/r.

Таким образом, уравнение сферической волны имеет вид

 = (b/r) cos (t – kx) (78.9)

где b – постоянная величина, численно равная амплитуде на расстоянии от источника, равном единице.

Следует учитывать сделанную выше оговорку о конечности размеров реальных источников колебаний: попытка устремить r к нулю некорректна не только с точки зрения математики, но и не соответствует действительности.