Уравнения Максвелла

Теория Максвелла объяснила все известные в то время экспериментальные факты и предсказала ряд новых явлений, существование которых подтвердилось впоследствии. Основным следствием теории был вывод о существовании электромагнитных волн, распространяющихся со скоростью света. Теоретическое исследование свойств этих волн привело Максвелла к созданию электромагнитной теории света.

Основу теории образуют уравнения Максвелла. В учении об электромагнетизме эти уравнения играют такую же роль, как законы Ньютона в механике или основные законы (начала) в термодинамике.

Первое из уравнений Максвелла связывает значения Е с изменениями вектора В во времени и является по существу выражением закона электромагнитной индукции.

Второе уравнение отражает то свойство вектора В, что его линии замкнуты (или уходят в бесконечность).

(108.1)

(108.2)

Третье уравнение устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем. Четвертое показывает, что линии вектора D могут начинаться и оканчиваться на зарядах:

(108.3)

(108.4)

(j здесь и в дальнейшем – плотность тока проводимости).

Перейти к уравнениям в дифференциальной форме можно с помощью сформулированных выше теорем Стокса и Остроградского – Гаусса.

Теорема Стокса [см. (107.14) ] применима к первому уравнению Максвелла. Поверхности интегрирования в правой и левой части одни и те же. Тогда уравнение (108.1) примет вид

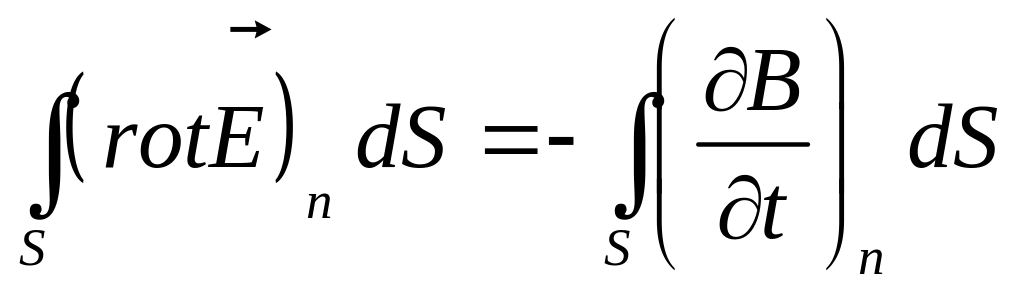
Поскольку поверхности справа и слева едины можно написать:

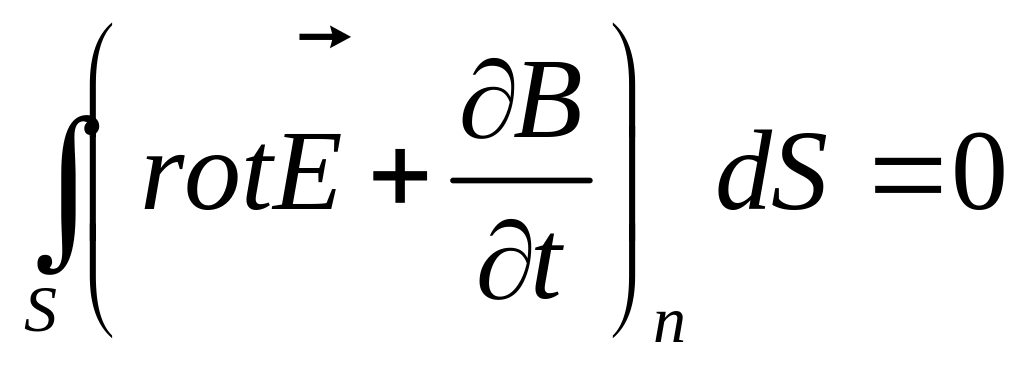
Так как поверхность S произвольна, равенство возможно лишь в случае равенства нулю подынтегрального выражения в любой точке пространства для произвольно ориентированной площадки dS. Тогда в каждой точке пространства

Применение теоремы Стокса к формуле (108.3) и повторение тех же рассуждений, показывает, что

Можно применить теорему Остроградского – Гаусса [см. (107.5) ] к левой части формулы (108.4):

При произвольном выборе объема V, равенство выполняется, когда подынтегральные выражения в обеих частях имеют в каждой точке пространства одинаковые значения, т. е,

div D = .

Применение теоремы Остроградского – Гаусса к формуле (108.2) дает

div В =0.

Итак, в дифференциальной форме уравнения Максвелла выглядят следующим образом:

(108.5)

(108.6)

(первая пара уравнений),

(108.7)

(108.8)

(вторая пара уравнений).

При решении этих уравнений используются также соотношения:

(108.9)

(108.10)

(108.11)

Совокупность семи уравнений (108.5) – (108.11) образует основу электродинамики покоящихся сред.

Третий семестр.

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Волновое уравнение

Переменное электрическое поле порождает магнитное, которое тоже оказывается переменным. Это переменное магнитное поле порождает электрическое поле и т. д. Таким образом, если возбудить с помощью зарядов переменное электрическое или магнитное поле, в окружающем пространстве возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке. Тот же процесс получится и при возбуждении поля переменными токами, создающими магнитное поле. Этот процесс может быть периодическим во времени и в пространстве и, следовательно, представлять собой волну. Доказательство возможности существования электромагнитных волн вытекает из уравнений Максвелла.

Напишем уравнения Максвелла для однородной нейтральной ( = 0) непроводящей (j = 0) среды с постоянными проницаемостями  и . В этом случае

Следовательно, уравнения (108.5) – (108.8) имеют вид

(109.1)

(109.2)

(109.3)

(109.4)

Применим к уравнению (109.1) операцию rot

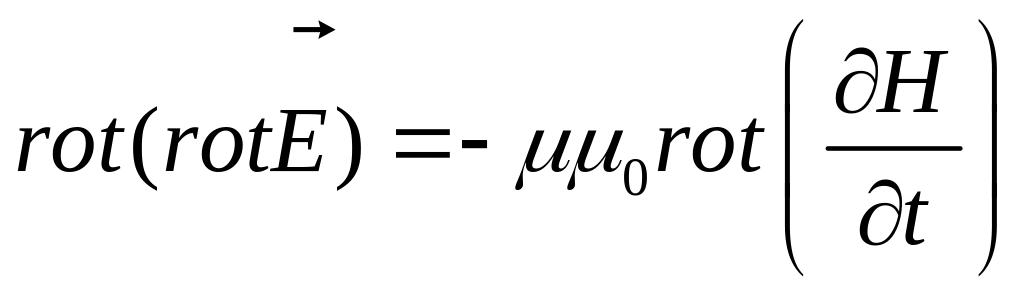(109.5)

По сути rot есть дифференцирование по координатам. Меняя порядок дифференцирования по координатам и времени, можно написать

Произведя в уравнении (109.5) эту замену и подставив в получившееся выражение значение (!09.3) для rot H, получим

(109.6)

Применив операцию rot к уравнению (109.3) и произведя аналогичные преобразования, придем к уравнению

(109.7)

В соответствии с (107.22) rot rot E = grad div E – ∆Е. При условии, выражаемом уравнением (109.4), первый член этого равенства обращается в нуль. Следовательно, левая часть формулы (109.6) может быть записана в виде –∆Е. Опустив в получающейся формуле знак минус слева и справа, придем к уравнению

или, расписав ∆Е,

(109.8)

Сходным образом уравнение (109.7) можно преобразовать к виду

(109.9)

Заметим, что уравнения (109.8) и (109.9) неразрывно связаны друг с другом, так как они получены из уравнений (109.1) и (109.3), каждое из которых содержит и Е и Н.

Уравнения полученного вида представляют собой волновые уравнения. Корень квадратный из величины, обратной коэффициенту при второй производной по времени, дает фазовую скорость этой волны:

(109.10)

Для вакуума по этой формуле получается

То есть, в вакууме фазовая скорость электромагнитных волн совпадает со скоростью света.