Дифракция. Принцип Гюйгенса – Френеля в оптике.

Интерференция есть перераспределение интенсивности волн в пространстве, наблюдаемое на некоторой поверхности. Дифракция, формально, есть явление огибания волной препятствий. Наблюдаемое проявление дифракции – интерференция разных пространственных масштабов. Объяснение этих явлений едино: принцип Гюйгенса – Френеля.

Исходно Гюйгенс предложил рассматривать процесс распространения света как совокупность сферических волн, создаваемых каждой точкой волнового фронта. Новый волновой фронт в данный момент времени рассматривается как огибающая этих сферических

волн. Вопрос о направлении распространения волны был решен рядом дополнительных положений, предложенных Френелем. Это позволило создать математический аппарат, способный описать явления физической оптики.

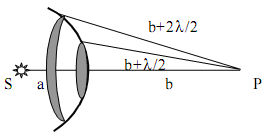
Распространение сферической волны от источника S в точку Р изображено на рисунке. Здесь источник света окружён сферой радиуса а и на этой поверхности  выделен участок d. По Френелю электрическое поле, создается в точке Р в результате интерференции волн, приходящих от источников d. Интенсивность волн зависит от величины d, расположения нормали к поверхности d и угла . Френель ввел в рассмотрение величину k(), имеющую максимальное значение при  = 0. Максимум величины k соответствует совпадению направления нормали и линии SP. При   /2 k = 0, то есть волна распространяется только “вперед” от источника.

Амплитуду колебаний поля, созданного в точке Р сферической волной, исходящей из элемента поверхности d, можно определить таким образом:

Результирующее поле в точке Р определяется принципом суперпозиции:

Это выражение есть математическое представление принципа Гюйгенса – Френеля.

Различают два вида дифракции:

дифракция в параллельных лучах (дифракция дальнего поля) – дифракция Фраунгофера

дифракция ближнего поля или дифракция Френеля.

Дифракция Френеля.

Практически очевидно, что расчеты с использованием формулы Гюйгенса – Френеля в общем случае весьма сложны. Можно отметить, что из теории дифракции появился ряд нестандартных интегралов, вычисление которых отнесено в курс математики. Упрощение нахождения результирующей амплитуды связано с появлением какой-либо симметрии.

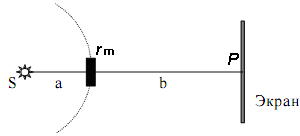
Например, можно рассмотреть и стандартно рассматривается определение амплитуды сферической волны, проходящей через круглое отверстие. Для начала можно принять, что диаметр отверстия очень велик, поэтому на рисунке оно не обозначено. Пусть источник S

излучает волну с длиной  в сторону точки наблюдения P. При этом можно выделить некоторую волновую поверхность и разделить ее на кольца так, чтобы расстояния от краев колец отличались по величине на  / 2. Полученные кольца являются зонами Френеля. Понятно, что волны от соседних зон приходят в точку Р в противофазе. Расстояние от зоны с номером m до точки Р равно b_m = b+m/2.

Поскольку энергия, излучаемая единицей площади каждой зоны одинакова, амплитуда волны, излучаемой каждой зоной, должна быть пропорциональна её площади. Площадь зоны m равна разности площадей, ограниченных сферическими сегментами m и m-1.

Из рисунка видно, что

Из второго равенства следует

При достаточно малых m второе слагаемое гораздо меньше первого и учитываться не будет. Площадь сферического сегмента, отмеченного на рисунке, равна , откуда с учётом предыдущего выражения получается:

,

кроме того,

, (*)

где принято, что a>>h_m. Таким образом, с указанной точностью площади всех зон равны!

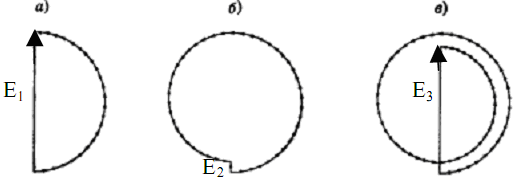
Однако следует помнить, что волна сферическая (Е  1/r), следовательно, её амплитуда падает по мере роста m, так как b_m = b+m/2. То есть E₁E₂E₃…. Суммарная амплитуда равна

Здесь учтена противофазность колебаний в точке Р, излучённых соседними зонами, а также малость различия амплитуд их колебаний. Последнее обеспечивает практически нулевое значение выражений в скобках.

Таким образом, если отверстие велико, преграды практически нет и вся волновая поверхность открыта, то интенсивность в точке Р равна

то есть в 4 раза меньше интенсивности при одной первой открытой зоне Френеля.

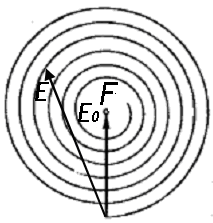
Изящную интерпретацию проведённого расчёта можно получить в виде так называемой спирали Френеля. Для её построения в полярных координатах, начиная от горизонтальной оси, в виде радиусов откладываются модули векторов от соседних точек волновой поверхности. Угловая координата равна разности фаз волны, дошедшей до точки Р от соответствующей нецентральной точки волновой поверхности и волны, пришедшей из центра волновой поверхности.

Результатом является спираль с радиусом, уменьшающимся по мере учёта точек всё более удалённых от центра волновой поверхности. На рисунке показан вид спирали при учёте точек первой, второй и третьей зон Френеля.

Теперь можно сравнительно просто проанализировать собственно дифракцию на круглом отверстии.

Дифракция возникнет, если на пути распространения волны поставить препятствие с круглым отверстием радиуса r_m. При этом, если расстояния a и b соответствуют полученному выше соотношению

,

отверстие будет заполнено числом зон Френеля равным m. В зависимости от этого числа при достаточно малых m интенсивность света в точке Р будет равна  4I₀ или 0. В случае нецелого

числа зон Френеля, вписываемых в отверстие, интенсивность в точке Р можно определить с помощью спирали Френеля (см. рисунок). На рисунке Е₀ есть амплитуда волны, определяемая всей волновой поверхностью без её ограничения отверстием, а Е – амплитуда, определяемая проходящей через отверстие частью волновой поверхности. Поскольку зоны Френеля создают налагающиеся друг на друга волны, в окрестности точки Р должна наблюдаться интерференционная картина симметрии, заданной симметрией преграды, то есть состоящая из системы концентрических светлых и тёмных колец. Если источник света не монохроматический, в интерференционной картине должны присутствовать все спектральные компоненты источника, что затруднит визуальное наблюдение дифракции.

Метод спирали Френеля обеспечивает определение интенсивности света только в точке Р.

С его же помощью можно рассмотреть эффект, выступивший как один из решающих доводов в пользу теории волновой оптики. Речь идёт о пятне Пуассона. Предположение об его существовании было высказано при рассмотрении дифракции на круглом диске и проверено опытом Араго.

Если на пути сферической волны поставить круглый диск без каких-либо дополнительных препятствий, то по логике, приведённой выше и подкреплённой анализом с использованием представлений о зонах Френеля (см. ниже), в точке Р должно наблюдаться светлое пятно вне зависимости от числа закрываемых зон.

При радиусе диска r_m результирующая амплитуда волны равна:

Таким образом, при достаточно малых m  10 , то есть в центре картины (в точке Р) имеется светлое пятно, интенсивность которого равна , то есть интенсивности при отсутствии преграды. Естественно, что никакие соображения, связанные с корпускулярной теорией света объяснить такой результат не могут.

Между тем, корпускулярная теория прекрасно объясняет результаты геометрической оптики. Следовательно, для того, чтобы волновая теория приобрела бы статус универсальной теории света необходимо определить критерий перехода от волновой оптики к оптике геометрической. Он определяется достаточно просто: необходимо сравнить размер препятствия с размером радиуса или диаметра зоны Френеля. В этом смысле величиной, выполняющей роль критерия получения разного рода дифракций или перехода от волновой оптики к геометрической становится число зон Френеля, заполняющих отверстие. При этом экспериментальная проверка возможна при работе только с точечным источником, то есть при достаточно большом расстоянии до источника: а>>b.

1. При сопоставимости размера первой зоны Френеля с диаметром отверстия (m  1) должна наблюдаться дифракция Френеля. Тогда . Можно обратить внимание на малость величины b, необходимую для наблюдения именно френелевской дифракции. Она объясняет и другое её название – дифракция ближнего поля.

2. Переход от волновой оптики к геометрической должен возникнуть при отсутствии условия наблюдения дифракции, то есть при очень большом числе зон Френеля (m >> 1), когда интерференционная картина становится неразличимой. Тогда .

3. При большом значении величины b наблюдается дифракция дальнего поля, отличающаяся тем, что в точке Р наблюдается только максимум интенсивности. Это происходит из-за того, что , то есть размер отверстия гораздо меньше радиуса первой зоны. Дифракцию дальнего поля называют чаще дифракцией Фраунгофера. Следует отметить, что при больших величинах a и b говорить о сферической волне не приходится – волновой фронт становится практически плоским.