Волна на границе двух сред.

Рассмотрим поведение световой волны на границе раздела двух однородных и изотропных прозрачных сред. Пусть волна распространяется первоначально в среде 1 с показателем преломления n₁. Для простоты будем считать, что граница раздела плоская и направление распространения волны перпендикулярно к этой плоскости. Достигнув поверхности раздела (поток положительный), волна частично пройдет в среду 2 с показателем преломления n₂ (поток положительный), частично же она отразится, в результате чего возникнет волна, распространяющаяся навстречу первоначальной (падающей) волне (поток отрицательный). Обозначим световой вектор падающей волны в непосредственной близости к границе раздела символом E₁, световой вектор прошедшей волны – символом Е₂ и световой вектор отраженной волны – символом E₁' (векторы Е₂ и E₁' рассматриваются, как и вектор Е₁, в непосредственной близости к границе раздела сред). Вследствие однородности и изотропности сред все три вектора лежат в одной плоскости (перпендикулярной к поверхности раздела сред).

В первой среде имеет место суперпозиция падающей и отраженной волн. Результирующее электрическое поле характеризуется вектором E₁' + Е₁. Во второй среде поле характеризуется вектором Е₂. Тангенциальные составляющие вектора Е в обеих средах должны быть одинаковыми:

(16.9)

Примем направление вектора Е₁ за ось х и спроектируем все световые векторы на эту ось. В соответствии с условием (16.9) получим:

(16.10)

При указанном выборе оси х проекция Е_1х положительна и равна модулю вектора Е₁. Определим знаки двух других проекций. Если знак проекции окажется положительным, это будет означать, что соответствующий вектор Е направлен в ту же сторону, что и Е₁ и, следовательно, колебания в падающей волне и в волне, характеризуемой данным Е, происходят на границе раздела в одинаковой фазе. Если же знак проекции окажется отрицательным, это будет означать, что векторы Е и Е₁ направлены в противоположные стороны, так что колебания в соответствующих волнах происходят на границе раздела в противофазе.

Энергия, которую несет с собой падающая волна, распределяется на границе раздела между волной, прошедшей во вторую среду, и отраженной волной. Следовательно (см. (16.8)):

(16.11)

Исключив E₁' из уравнений (16.10) и (16.11), можно прийти к соотношению

Так как , . Следовательно, векторы , и сонаправлены и на границе раздела их фаза не претерпевает скачка.

Исключив из уравнений (16.10) и (16.11) , легко определить :

(16.12)

Отсюда следует, что при n₂ < n₁ знак совпадает со знаком . То есть колебания в падающей и отраженной волнах происходят на границе раздела синфазно – фаза волны при отражении не изменяется. Если же n₂ > n₁ то знак противоположен знаку , колебания в падающей и отраженной волнах происходят на границе раздела в противофазе – фаза волны при отражении изменяется скачком на . Полученный результат справедлив и при наклонном падении волны на границу раздела двух прозрачных сред.

Вывод. При падении света из среды 1 на границу со средой 2 отраженная волна меняет фазу на  при n₂ > n₁. При n₂ < n₁ такого изменения фазы не происходит.

Выражение (16.12) определяет связь между отраженной и падающей волнами, что позволяет сразу найти коэффициент отражения R световой волны для случая ее нормального падения на границу раздела двух сред.

По определению

где – отношение интенсивностей отраженной и падающей волн. Отношение определим из (16.12). Получим:

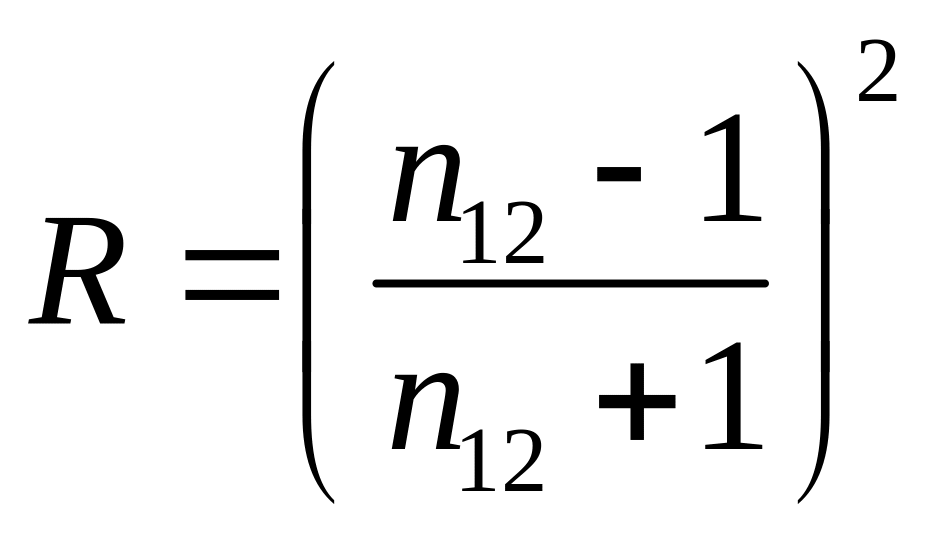(16.13)

(n₁₂ = n₂/ n₁ – показатель преломления второй среды по отношению к первой). Отметим, что коэффициент отражения при нормальном падении волны на границу раздела сред не зависит от направления падения волны: замена n₁₂ в формуле (16.13) на обратную величину n₂₁= 1/ n₁₂ не изменяет значения R.

Аналогичным образом определяется коэффициент проникновения волны T во вторую среду:

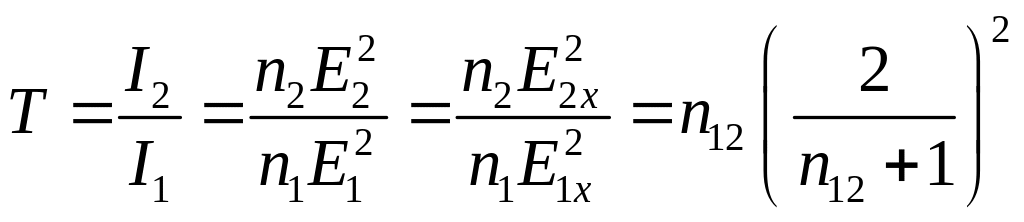(16.14)

Сумма выражений (16.13) и (16.14) равна единице, что соответствует принципу сохранения энергии (сохранению светового потока).

Для оценки порядка величины коэффициента отражения используем показатель преломления стекла n  1,5. Из (16.13) получим R = 0,04. Таким образом, каждая поверхность прозрачной пластинки отражает при нормальном падении лишь несколько процентов падающего светового потока.

Интерференция световых волн

Пусть две волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления:

A₁ cos (t + ₁),

А₂ cos (t + ₂).

Амплитуда результирующего колебания в данной точке может быть определена с помощью векторной диаграммы.

Тогда:

Если разность фаз возбуждаемых волнами колебаний остается постоянной во времени, то волны, как и их источники, называются когерентными.

В случае некогерентных волн изменяется, принимая с равной вероятностью любые значения. Тогда среднее по времени значение равно нулю. В этом случае .

Отсюда следует, что интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой из волн в отдельности:

(17.1)

В случае когерентных волн имеет постоянное во времени (но свое для каждой точки пространства) значение, так что

(17.2)

В тех точках пространства, для которых , ; в точках, для которых , . Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн. Особенно отчетливо проявляется интерференция в том случае, когда интенсивность обеих интерферирующих волн одинакова: . Тогда согласно (17.2) в минимумах , в максимумах же . Для некогерентных волн при том же условии получается всюду одинаковая освещенность .

Сказанное объясняет причину отсутствия интерференции от обычных источников света, например, ламп накаливания. Эти источники не когерентны. Излучение светящегося тела складывается из волн, испускаемых атомами тела. Эксперимент показывает, что излучение отдельного атома продолжается около 10^–8 сек. За это время успевает образоваться последовательность горбов и впадин (или, как говорят, цуг волн) протяженностью примерно 3 м. «Погаснув», атом через некоторое время «вспыхивает» вновь. Однако фаза нового цуга волн никак не связана с фазой предыдущего цуга. Кроме того, одновременно «вспыхивает» большое количество атомов. Возбуждаемые ими цуги волн, налагаясь друг на друга, образуют испускаемую телом световую волну. В этой волне излучение одной группы атомов через время порядка 10^–8 сек сменяется излучением другой группы, причем фаза результирующей волны претерпевает случайные скачкообразные изменения.

Понятие когерентности в реальной (экспеиментаьной) ситуации требует более обстоятельного понимания. Световые волны, описываемые, например, уравнениями:

A cos(t – kx + ) или (A/r) cos(t – kx + )

с постоянными A, k и , являются абстракцией. В реальной световой волне её параметры, в частности фаза , изменяются беспорядочным образом с течением времени, а также при перемещении от одной точки пространства к другой.

Чтобы рассмотреть изменение фазы  с течением времени t, необходимо ввести время когерентности , определив его как время, за которое случайное изменение фазы достигает значения ~ . За время  колебание как бы забывает свою первоначальную фазу и становится некогерентным по отношению к самому себе. Из сказанного выше об излучении естественного источника света ясно, что время когерентности световой волны, испускаемой таким источником, ~ 10^–8 сек. Время когерентности называют также продолжительностью цуга волн. За время  волна проходит путь с, который представляет собой длину цуга (иногда эту величину называют длиной когерентности). На длине цуга случайные изменения фазы достигают величины ~ .

При  ~ 10^–8 сек длина цуга составляет ~3м.

При переходе от одной точки пространства к другой фаза также меняется. В идеальной плоской или сферической волне  одинакова во всех точках плоскости х = const или сферы r = const. Эти плоскости и сферы обычно называются волновыми поверхностями. В реальной световой волне фаза  при переходе от одной точки «волновой поверхности» к другой каким-то образом изменяется, то есть само понятие «волновая поверхность» теряет смысл. Поэтому в рассмотрение вводится расстояние l, при смещении на которое вдоль «волновой поверхности» случайное изменение фазы достигает значения ~ . Колебания в двух точках «волновой поверхности», отстоящих друг от друга на расстояние, меньшее l, будут приблизительно когерентными. Такого рода когерентность называется пространственной. Все пространство, занимаемое волной, можно разбить на части, в каждой из которых волна сохраняет когерентность. Объем такой части пространства, называемый объемом когерентности, по порядку величины равен произведению длины цуга на площадь круга диаметра l.

Пространственная когерентность световой волны вблизи поверхности излучающего ее нагретого тела ограничивается размером l всего в несколько длин волн. Это вызвано тем, что разные участки нагретого тела излучают независимо друга от друга. По мере удаления от источника степень пространственной когерентности возрастает. Излучение лазера обладает огромной пространственной когерентностью. У выходного отверстия лазера пространственная когерентность наблюдается во всем поперечном сечении светового пучка.

Кратко можно сказать, что когерентностью называется согласованное протекание нескольких колебательных или волновых процессов. Согласованность, заключающаяся в том, что разность фаз двух колебаний остается неизменной с течением времени в данной точке пространства, называется временнόй когерентностью. Согласованность, заключающаяся в том, что остается постоянной разность фаз колебаний, происходящих в разных точках «волновой поверхности», называется пространственной когерентностью.

Выше было выяснено, что естественные источники света не когерентны. Когерентные световые волны можно получить, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником, на две части. Если заставить эти две волны пройти разные оптические пути, а потом наложить их друг на друга, наблюдается интерференция. Разность оптических длин путей, проходимых интерферирующими волнами, не должна быть очень большой, так как складывающиеся колебания должны принадлежать одному и тому же результирующему цугу волн. Если эта разность будет порядка 3 м (см. выше), наложатся колебания, соответствующие разным цугам, и разность фаз между ними будет непрерывно меняться хаотическим образом.

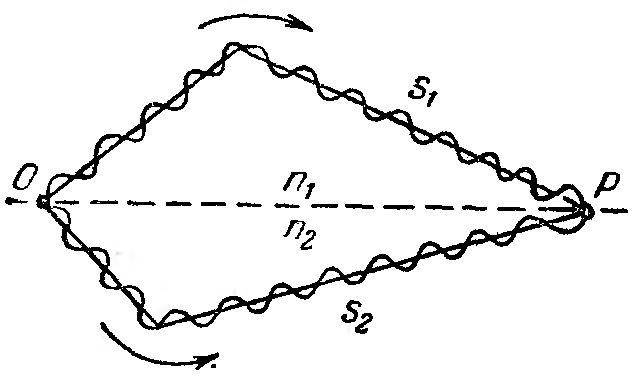
Пусть разделение на две когерентные волны происходит в точке О (рис. 42). До точки Р первая волна проходит в среде с показателем преломления n₁ путь s₁, вторая волна проходит в среде с показателем преломления n₂ путь s₂. Если в точке О фаза колебания равна t, то первая

Рис. 42.

волна возбудит в точке Р колебание

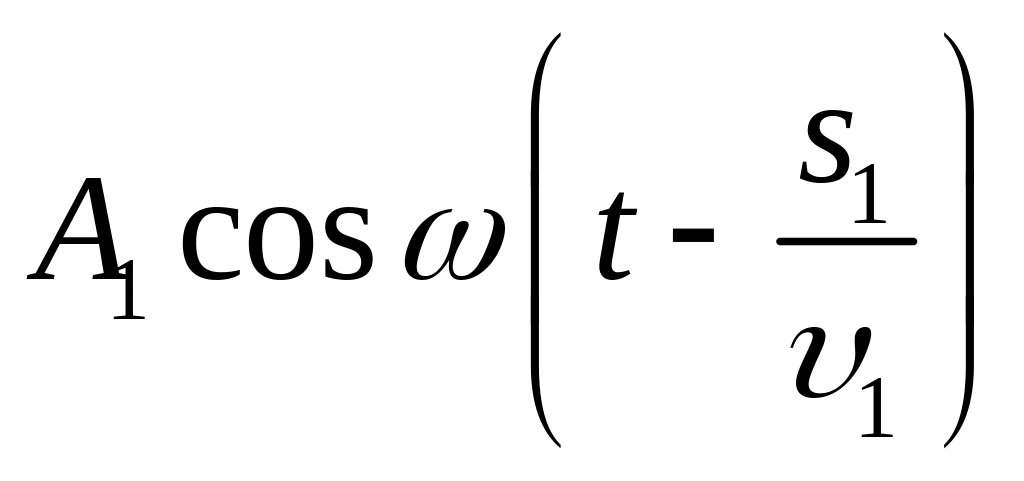
а вторая волна – колебание

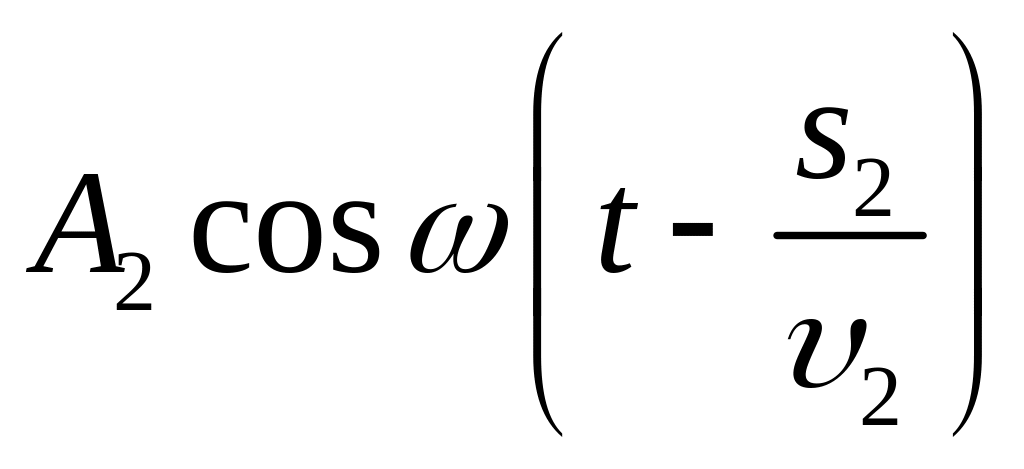
где ₁ = c/n₁ и ₂ = c/n₂ – фазовая скорость первой и второй волны. Следовательно, разность фаз колебаний, возбуждаемых волнами в точке Р, будет равна

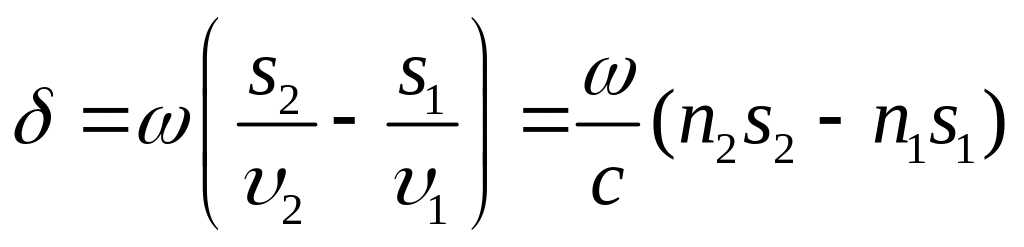
Заменив /с через 2v/с = 2/₀, (₀ – длина волны в вакууме), выражению для разности фаз можно придать вид:

(17.3)

где

(17.4)

– величина, равная разности оптических длин проходимых волнами путей и называемая оптической разностью хода.

Из формулы (17.3) видно, что если оптическая разность хода  равна целому числу длин волн в вакууме:

(17.5)

то разность фаз  оказывается кратной 2 и колебания, возбуждаемые в точке Р обеими волнами, будут происходить с одинаковой фазой. Следовательно, условие (17.5) есть условие интерференционного максимума.

Если  равна полуцелому числу длин волн в вакууме:

(17.6)

то  = ± (k2 + ), так что колебания в точке Р находятся в противофазе. Таким образом, условие (17.6) есть условие интерференционного минимума.