Распространение света в средах.

Общие положения. Среду, в которой распространяется волна, стандартно считают однородной и изотропной.

При распространении ЭМВ электрическая компонента действует на электроны среды (оптические электроны). При этом они двигаются вдоль направления вектора . Характер движений соответствует обычным малым вынужденным колебаниям. Энергия взаимодействия компоненты волны с магнитными моментами электронов гораздо меньше энергии взаимодействия зарядов электронов с компонентой . Поэтому влиянием магнитной составляющей волны на поведение электронов обычно пренебрегают.

Если колеблются связанные электроны, собственная частота колебаний которых достаточно удалена от частоты ЭМВ, то потери мощности волны, прошедшей через среду, малы (случай прозрачного диэлектрика).

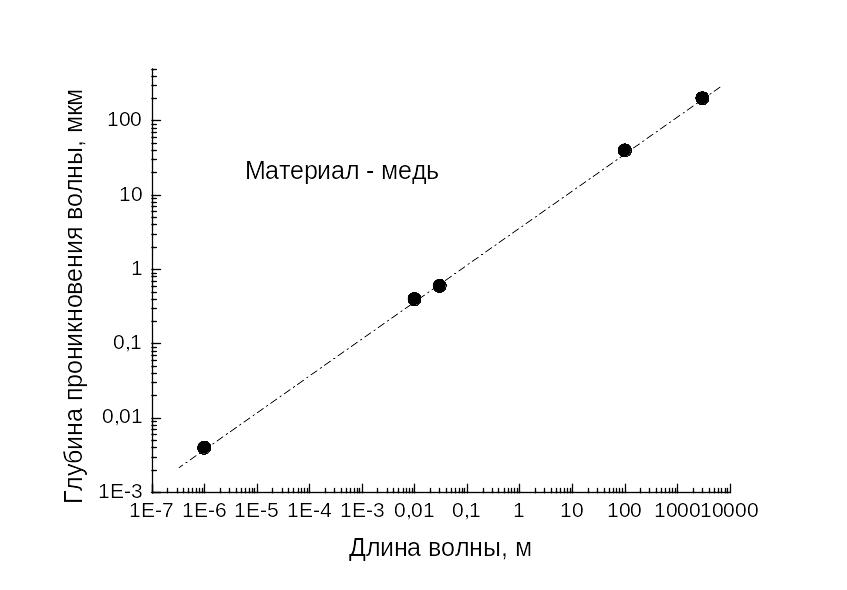
Обратный случай – распространение ЭМВ в металлах, в которых имеется значительная концентрация свободных электронов. Их движение под действием электрической компоненты ЭМВ эквивалентно протеканию токов с частотой равной частоте колебаний вектора . Соответственно, энергия колебаний большого числа электронов преобразуется в джоулево тепло, что объясняет экспоненциальное уменьшение мощности волны, распространяющейся в сторону от поверхности металла. Феноменологически это означает существование зависимости характерной глубины проникновения (т.н. скин-слой)  электромагнитной волны в металл от длины волны . На рисунке приведена такая зависимость для меди.

Характерное расстояние между атомами в твердом теле составляет 0.2 нм (2 Å). Это означает, что световая волна возбуждает колебания электронов на расстоянии от поверхности меди приблизительно равном 20 слоям атомов. На бóльших расстояниях волна практически полностью затухает. Поэтому металлы рассматриваются как среды с большим затуханием ЭМВ.

Рассматривая взаимодействие электронов металла с ЭМВ, необходимо также представлять себе крайне малую эффективность передачи энергии волны от одного слоя атомов к соседнему. Можно рассмотреть механический аналог такого процесса. Действительно, возбуждение колебаний слабо демпфированных осцилляторов (например, оптических электронов в прозрачных диэлектриках) осуществляется достаточно просто. Теория слабо затухающих малых колебаний хорошо известна. Однако сильное затухание соответствует сильной связи осциллятора с соседним объектом, препятствующим колебаниям. В предельном случае осциллятор представляет собой единое целое с этим объектом. В этом случае серьезно затруднена передача импульса колебаний и, следовательно, энергии соседнему осциллятору. Следовательно, поглощаемая доля энергии ЭМВ, падающей на поверхность металла, мала. Основная ее часть отражается от поверхности.

Таким образом, значительное прохождение волны вглубь металла невозможно в силу значительных потерь мощности в металлах. При падении ЭМВ на металлическую поверхность следует ожидать лишь ее отражения. В случае слабых потерь энергии колебаний электронов, то есть при падении ЭМВ на границу диэлектрика, следует ожидать появления отраженной волны и волны, распространяющейся в среде (преломленной). В этом смысле следует подчеркнуть, что среды с малыми потерями, например, стекло, в состоянии поглотить всю мощность волны при достаточной толщине слоя среды. Напротив, при падении волны на среду с большими потерями (металл) интенсивность волны изменяется слабо (волна отражается).

Математически колебания вектора в плоской волне представляются таким образом:

или, с использованием мнимой экспоненты:

(1)

Здесь – амплитуда волны,  – частота колебаний компонент электромагнитного поля,

k =  /  =  n/c = k n = 2 / (2)

– модуль волнового вектора в среде, направление которого совпадает с направлением распространения ЭМВ. Величина  – фазовая скорость волны в среде, то есть скорость распространения плоскости с одинаковой фазой колебаний векторов и .  – длина волны в среде. В дальнейшем мы будем считать, что волна распространяется в плоскости x,y ( ) и, следовательно:

В случае распространения волны в среде с потерями вводится комплексный показатель преломления вещества . Тогда выражение, описывающее распространение плоской волны, путем преобразований приобретет вид:

Здесь - волновой вектор волны в среде с потерями, - волновой вектор волны в вакууме, - вектор волны в среде без потерь, но с тем же показателем преломления n,  - показатель затухания волны. Преобразования проведены с использованием трех первых равенств выражения (2).

Видно, что потери, учтенные с помощью комплексного показателя преломления, в согласии с законом Бугера, проявляются в экспоненциальном затухании амплитуды волны, распространяющейся в направлении .