25. Построение поверхностей

Параметрическое задание поверхности: P(u,w) = [x(u,w),y(u,w),z(u,w)].

P(u,w) – вектор, полученный по известным или входным данным;

Q(u,w) – вектор конструируемой поверхности.

Билинейные поверхности

Заданы P(0, 0)P(0, 1)P(1, 0)P(1, 1) – угловые точки поверхности,

Q(u, w) = P(0, 0) (1 – u)(1–w) + P(0, 1) (1 – u) w + P(1, 0) u (1–w) + P(1, 1) u w (1)

или Q(u, w) = [(1–u) u] P(0, 0) P(0, 1) 1–w

P(1, 0)P(1, 1)w,u,wЄ [0, 1]

Линейчатые поверхности

Заданы две граничные кривые: P(u, 0) иP(u, 1). Тогда линейная интерполяция между этими кривыми:

Q(u,w) =P(u, 0) (1 –w) +P(u, 1)w(2)

При этом: Q(u, 0) =P(u, 0),Q(u, 1) =P(u, 1).

Если предположить, что известны P(0,w) иP(1,w), то линейчатая поверхность будет:

Q(u,w) =P(0,w) (1 –u) +P(1,w)u(3)

При этом: Q(0,w) =P(0,w), иQ(1,w) =P(1,w).

Линейные поверхности Кунса

Известны четыре граничные кривые: P(u, 0),P(u, 1),P(0,w) иP(1,w).

Суммируя уравнения (2) и (3) получим:

Q(u,w) =P(u, 0) (1 –w) +P(u, 1)w+P(0,w) (1 –u) +P(1,w)u(4)

Однако анализ показывает, что в угловых точках и на границе получаем несоответствие исходным данным, т.е. Q(0, 0) =P(0, 0) +P(0, 0);Q(0,w) =P(0, 0)(1 –w) +P(0, 1)w+P(0,w) .

Исследование уравнения (4) показывает, что несоответствие возникает из-за того, что угловые точки просчитываются дважды. Например, P(0, 0) содержится в описании граничных кривых

P(u, 0) иP(0,w). Поэтому для правильного результата необходимо вычесть лишние угловые точки, т.е.:

Q(u,w) =P(u, 0) (1 –w) +P(u, 1)w+P(0,w) (1 –u) +P(1,w)u–P(0, 0)(1 –w)(1 –u) –

– P(0, 1)(1 –u)w–P(1, 0)u(1 –w) –P(1, 1)uw(5)

В матричной форме его можно записать так:

– P(0, 0) – P(0, 1) P(0, w) 1 – w

Q(u, w) = [1–u u 1] –P(1, 0) –P(1, 1) P(1, w) w (6)

P(u, 0)P(u, 1) 0 1

Функции (1 – u),u, (1 –w) называются весовыми функциями.

Участок бикубической поверхности

Используем параметрический многочлен 3-го порядка для описания граничных кривых

P(u, 0),P(u, 1),P(0,w) иP(1,w): (7)

Пусть 0 ≤t≤ 1. Производная от многочлена:

(8)

П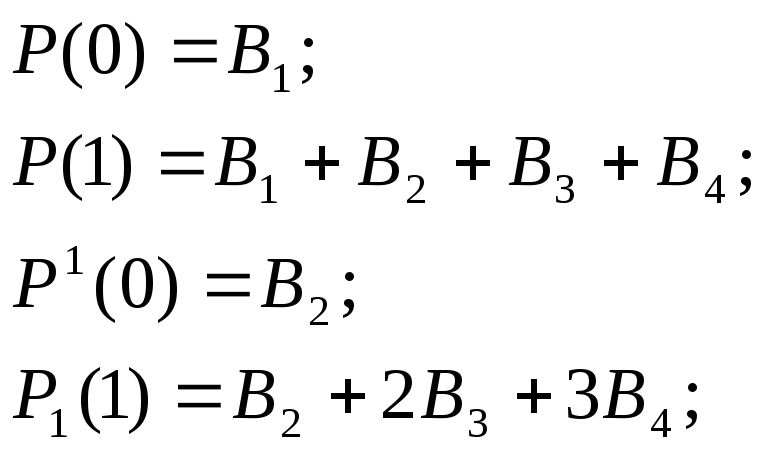олагая в (7) и (8)t=0 илиt=1 получаем:

Вматричной форме:

ИлиP = M B. Отсюда

Где Подставляя (11) в (7) получаем:

Или в общем случае, считая tпараметром,

Будем строить также как билинейный участок. Сначала построим поверхность удовлетворяющую граничным условиям на краях u= 0 иu= 1, затем поверхность, удовлетворяющую граничным условиямw= 0 иw= 1.Для получения бикубического участка объединим эти результаты. Тогда для первой линейчатой поверхности:

Приu=0Q(u,w) =P(0,w), т.е. удовлетворяет граничным условиям. Аналогично, линейчатая кубическая поверхность, удовлетворяющая граничным условиям на краях приw=const, будет:

Таким образом, бикубический участок поверхности характеризуется четырьма кубическими весовыми функциями F, четырьма граничными кривыми, четырьма угловыми точками, восемью касательными и четырьма векторами кривизны.

27. Отсечение нелицевых граней

Пусть у нас есть объект, внутри которого камера заведомо не окажется. Обычно такие объекты составляют большую часть или всю сцену. Тогда для каждой грани мы можем увидеть только одну ее сторону - лицевую. Грань - плоскость, она делит все 3D пространство на два полупространства. Так вот,лицевую сторону видно только из одного полупространства, из того, в которое "смотрит" нормаль к этой грани, направленная *из* объекта.Проверив, в какое полупространство попадает камера, можно сразу определить, является ли грань лицевой (то есть, может ли камера увидеть лицевую сторону этой грани) и надо ли ее рисовать.

Пусть грань имеет вершины v1, v2, v3 и нормаль (nx,ny,nz). Тогда уравнение плоскости, в которой она лежит, будет иметь вид

nx*x+ny*y+nz*z+d = 0.

d находим из того факта, что v1 в плоскости лежит:

nx*v1.x+ny*v1.y+nz*v1.z+d = 0,

d = -(nx*v1.x+ny*v1.y+nz*v1.z).

Функция nx*x+ny*y+nz*z+dпринимает положительные значения по одну сторону от плоскости, отрицательные по другую и равна нулю на самой плоскости. Точка (v1.x+nx,v1.y+ny,v1.z+nz) лежит, очевидно, в том полупространстве, откуда грань видно. Значение функции (назовем ее функцией видимости) в этой точке равно

nx*(v1.x+nx)+ny*(v1.y+ny)+nz*(v1.z+nz)+d =

nx*(v1.x+nx)+ny*(v1.y+ny)+nz*(v1.z+nz)-(nx*v1.x+ny*v1.y+nz*v1.z) =

nx*nx+ny*ny+nz*nz > 0.

Таким образом, если значение функции в какой-то точке больше нуля, то грань из этой точки потенциально видна. Нас интересует видимость грани из нашей камеры, а камера у нас зафиксирована в точке (0,0,-dist). Таким образом, получаем, что грани, для которых

-nz*dist-(nx*v1.x+ny*v1.y+nz*v1.z) < 0,

или, что равносильно,

nz*dist+nx*v1.x+ny*v1.y+nz*v1.z > 0,

заведомо не видны и время на их обработку и отрисовку тратить не стоит.

Отдельный вопрос - как считать нормали к граням. Точнее, как выбрать одну из двух нормалей, которая будет смотреть из объекта. Обычно эта проблема решается еще на этапе построения 3D моделей - например, пакет 3D Studio записывает вершины граней в порядке A-B-C так, чтобы векторное произведение BA*CA и было нормалью. Еще один способ -выбрать внутренную точку для объекта (либо вручную, либо взять его центр тяжести, либо еще как-нибудь - методов может быть придумано сколько угодно) и использовать ее: если для этой точки функция видимости положительна, то есть грань якобы видна, то надо поменять знак nx, ny и nz.

Осталось отметить, что для выпуклых объектов этот метод полностью решает задачу об удалении невидимых частей. Для невыпуклых же он позволяет быстро и просто сократить число граней, подлежащих дальнейшей проверке на видимость и собственно отрисовке.