10. Упругая сила, закон Гука.
Сила упругости.
Эти силы возникают в деформированном образце и направлены в сторону противоположную деформации.
Деформация— изменение формы и размеров тела.
Виды деформаций:
а) деформация растяжения и сжатия;
(линейные деформации)
Характеризуется абсолютным удлинением (∆l=l-l0 [м])
Относительное удлинение ε
б) деформация изгиба:
в) сдвига:
г) кручения
Рассмотрим растяжение и сжатие.
Механическое
напряжение при этом вводится (σ)
Диаграмма механических напряжений:
—
закон
Гука
Е—
модуль Юнга
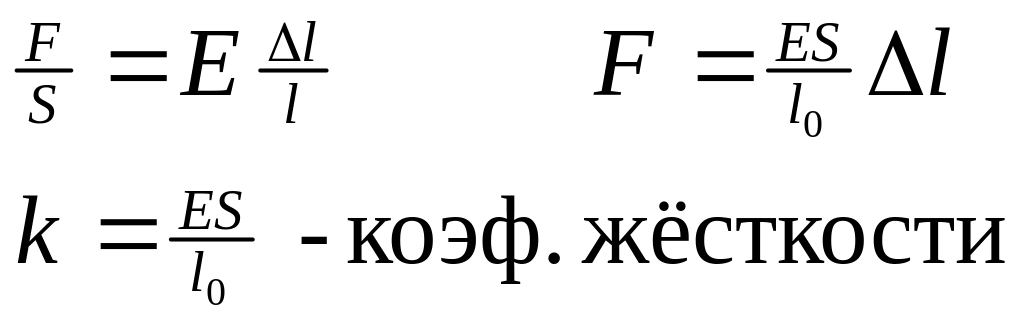
Сила направленная в сторону противоположную деформации
1-2— область упругих деформаций;
2-3— область неупругих деформаций;
3-4— область текучести материалов;
5— предел прочности;
Замечание:
При последовательном соединении пружин
При параллельном
11.Работа силы. Кинетическая энергия.
При прямолинейном движении и постоянном значении силы работа равна произведению величины проекции вектора силы на направление движения и величины пройденного пути:
При
этом действующая сила F
и вектор скорости v
процесса γ
за всё время наблюдения Δt
постоянны, работа численно равна
,
в противном случае она вычисляется как
интеграл:
.
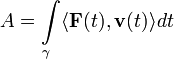Как следствие, если движение процесса ортогонально силе F, её работа равна нулю.
Кинетическая энергия.
Энергия это физическая величина, характеризующая способность систем тел совершать работу. Механическая энергия делится на кинетическую и потенциальную. E=Eк+Eп. Кинетическая энергия тела является мерой его механического движения и измеряется той работой, которую может совершить это тело при его торможении до полной остановки. Кинетическая энергия материальной равна половине произведения массы m точки на квадрат скорости ее движения: Ек=½mv2 . – при поступательном движении.
12. Закон сохранения энергии
Закон сохранения энергии — фундаментальный закон природы, заключающийся в том, что энергия замкнутой системы сохраняется во времени. Энергия не может возникнуть из ничего и не может в никуда исчезнуть, она может только переходить из одной формы в другую. В классической механике закон проявляется в сохранении механической энергии (суммы потенциальной и кинетической энергий). Частный случай — Закон сохранения механической энергии — механическая энергия консервативной механической системы сохраняется во времени. Проще говоря, при отсутствии сил типа трения механическая энергия не возникает из ничего и не может никуда исчезнуть. В замкнутой системе полная механическая энергия этой системы остается величиной постоянной Wполн=Wk+Wn Wk+Wn = const
Закон сохранения энергии — это интегральный закон. Это значит, что он складывается из действия дифференциальных законов и является свойством их совокупного действия. З.с.э отражает понятие однородности времени. Не важно в какой момент времени рассматривается система, з. для нее будет выполнятся. Можно добавить к законам сохранения массы.