
- •2)Гипотеза кварков.
- •2)Почему трением электризуются только разнородные вещества?
- •3)Почему трением практически невозможно наэлектризовать проводники? §2.Закон кулона
- •§3. Напряженность электростатического поля. Полевая трактовка закона кулона. Принцип суперпозиции.
- •§4 Линии вектора напряженности. Поток вектора напряженности.
- •2)Изобразить поле двух равных по величине положительных точечных зарядов;
- •4)Изобразить качественно поле:
- •§5 Теорема остроградского-гаусса.
- •3.Используя теорему Остроградского-Гаусса, получить формулу для расчета напряженности в произвольной точке поля заряда q равномерно распределенного по поверхности сферы.
- •6 Дифференциальная форма теоремы остроградского- гаусса
- •§7 Работа сил электростатического поля по перемещению заряда. Теорема о циркуляции вектора напряженности.
- •§8. Разность потенциалов, потенциал электростатического поля.
- •§9 Связь напряженности и разности потенциалов.Эквипотенциальные поверхности.
- •§11 Поле электрического диполя.
- •Тема II. Электростатическое поле при наличии проводников. §12 электрическое поле заряженного проводника.
- •13. Электростатическая индукция.
- •§14 Электрическая емкость уединенного проводника и системы проводников.
- •Тема III. Электрическое поле при наличии диэлектриков. §15 классификация диэлектриков.
- •§ 16 Диполь в электрическом поле.
- •17. Вектор поляризации и связанные заряды.
- •§ 18. Теорема остроградского – гаусса для вектора напряженности в диэлектриках. Вектор электрического смещения.
- •§ 19. Диэлектрическая восприимчивость и диэлектрическая проницаемость.
- •§ 20 Граничные условия.
- •§ 21 Сегнетоэлектрики.
- •Тема IV. Энергия электростатического взаимодействия. §22.Энергия взаимодействия системы неподвижных точечных зарядов.
- •§23 Энергия непрерывно распределенных зарядов, энергия заряженного проводника, конденсатора.
- •§ 24 Энергия электростатического поля, энергия взаимодействия заряженных тел.
- •Тема V. Стационарный электрический ток. § 25. Сила и плотность тока.
- •26. Уравнение непрерывности.
- •§ 27. Экспериментальные законы стационарного тока.
- •§ 28 Законы ома и джоуля – ленца в дифференциальной форме.
- •§ 29. Условия существования стационарного тока. Электродвижущая сила.
- •§ 30. Поле постоянного тока.
- •§ 31. Закон ома для замкнутой цепи.
- •§ 32. Правила кирхгофа для линейных разветвленных цепей.
- •§ 33. Квазистационарные токи.
- •Тема VI. Магнитное поле стационарного тока в вакууме. § 34. Закон взаимодействия элементов тока. Вектор магнитной индукции.
- •§ 35. Закон ампера. Сила лоренца.
- •§ 36 Линии вектора магнитной индукции. Теорема о полном магнитном потоке.
- •§ 37. Теорема о циркуляции вектора магнитной индукции. Вихревой характер магнитного поля.
- •§ 38.Контур с током в магнитном поле.
- •Тема VII. Магнитное поле в веществе. § 39. Источники магнитного поля в веществе. Вектор намагничивания.
- •§ 40. Связь молекулярных токов с вектором намагничивания.
- •§ 41. Теорема о циркуляции вектора магнитной индукции в магнетиках. Напряженность магнитного поля.
- •§ 42 Магнитная восприимчивость. Магнитная проницаемость. Источники линий напряженности.
- •§ 43. Граничные условия для векторов напряженности и магнитной индукции.
- •Тема VIII. Нестационарное магнитное поле. § 44. Явление электромагнитной индукции.
- •§ 45 Природа сторонних сил при явлении электромагнитной индукции.
- •§ 46. Явление самоиндукции.
- •§ 47. Взаимная индукция.
- •§ 48 Энергия магнитного поля.
- •Тема IX. Цепи переменного тока. § 49. Колебательный контур. Свободные элетромагнитные колебания в идельном контуре.
- •§ 50 Свободные колебания в контуре с активным сопротивлением.
- •§ 51. Цепь переменного тока с различной нагрузкой.
- •§ 52 Последовательная цепь переменного тока со смешанной нагрузкой.
- •§ 53. Энергия и мощность в цепи переменного тока.
- •§ 54 Разветвленная цепь переменного тока. Метод проводимостей.
- •§ 55.Вынужденные электромагнитные колебания. Резонанс напряжений.
- •§ 56 Резонанс токов.
- •§ 57.Трехфазный ток.
- •Тема X. Магнетики § 58 магнитомеханические явления.
- •§ 59 Диамагнетизм. Ларморова прецессия.
- •§ 60 Парамагнетики.
- •Самостоятельно: §61 ферромагнетики. Тема XI. Электромагнитное поле § 62 . Обобщения максвелла. Ток смещения.
- •§ 63 Полная система уравнений максвелла. Теория максвелла и границы ее применимости.
- •§ 64. Электромагнитные волны и их свойства.
- •§ 65. Закон сохранения энергии электромагнитного поля. Поток энергии.
- •§ 66. Излучение электромагнитных волн.
- •§ 67 Экспериментальные подтверждения теории максвелла: опыты герца и лебедева.
- •Тема XII. Электропроводность веществ. § 68. Классическая теория электропроводности металлов (друде-лоренца) и ее затруднения.
- •§69.Основные понятия зонной теории проводимости твердых тел.
- •§ 70 Собственная и примесная проводимость полупроводников,
- •§ 71 Работа выхода. Контактные явления в металлах.
- •§ 72 Контакт полупроводников с различным типом проводимости.
- •§ 73 Термоэлектрические явления.
§8. Разность потенциалов, потенциал электростатического поля.
Как известно работа сил потенциального поля равна убыли потенциальной
энергии:
![]()
Если разделить обе части этого выражения на величину переносимого пробного заряда, то можно ввести энергетическую характеристику двух точек поля.
Разностью потенциалов между двумя точками электростатического поля называется скалярная физическая величина, численно равная работе сил поля по перемещению единичного положительного заряда между двумя этими точками.
![]()
Потенциал точки поля, равный
потенциальной энергии единичного
положительного заряда в данной точке
поля, можно определить только через
потенциальную энергию в другой точке:
![]()
Если пробный заряд находится в точке 2 на очень большом расстоянии от заряда создающего поле, то они практически не взаимодействуют, так как кулоновская сила убывает обратно пропорционально квадрату расстояния.
Потенциальная энергия – энергия взаимодействия, а значит, потенциальная энергия пробного заряда в этом случае равна нулю.
Следовательно, можно принять, так называемое условие нормировки, что при r W0 и соответственно потенциал бесконечно удаленной точки поля равен нулю:
![]() при
при
![]()
Потенциалом точки электростатического поля называется скалярная физическая величина, численно равная работе сил поля по перемещению единичного, положительного заряда из этой в бесконечно удаленную точку.
Или:
![]() при
при
![]()
Таким образом, разность потенциалов – однозначная характеристика двух точек поля, а потенциал – неоднозначная характеристика, зависящая от условия нормировки.
Потенциал и разность потенциалов измеряются в: 1-2==1В
Получим формулу для вычисления потенциала поля точечного заряда:
![]() или
или
![]()
Если пробный заряд перемещается
в поле, созданном несколькими точечными
зарядами, то работа будет определяться
силой, действующей на него со стороны
результирующего поля:
![]()
Отсюда следует принцип суперпозиции для потенциала -
потенциал точки поля, созданного
несколькими точечными зарядами равен
алгебраической сумме потенциалов:
![]()
Если заряд распределен по некоторому объему с объемной плотностью x,y,z), то можно найти потенциал точки поля, используя формулу для поля точечного заряда и принцип суперпозиции.
Выделим такой малый объем dV, что заряд этого объема можно считать точечным. Тогда: dq=dV
Потенциал создаваемый этим зарядом в
точке поля :
![]()
Проинтегрировав по всему объему, найдем
потенциал точки поля, создаваемый всем
распределенным зарядом:
![]()
§9 Связь напряженности и разности потенциалов.Эквипотенциальные поверхности.
Выразим работу сил поля через разность
потенциалов А12=qn( 1-2)
и сравним с раннее полученной формулой
![]()
Соотношение между разностью потенциалов
и напряженностью поля в интегральной
форме:
![]()
Соответственно, потенциал точки поля
рассчитывается по формуле:
![]()
Найдем связь между напряженностью и
потенциалом в дифференциальной форме.
Для поля, силы которого потенциальны:
![]()
Поле точечного заряда зависит лишь от
расстояния, поэтому можно записать,
что:
![]()
Тогда:
![]()
Отсюда следует, что вектор напряженности всегда направлен в сторону убывания потенциала.
Используем:
,
,
![]()
Кроме линий напряженности для изображения электростатического поля используются эквипотенциальные поверхности.
Эквипотенциальная поверхность – геометрическое место точек равного потенциала, т.е. const.
1)Чтобы поверхность была эквипотенциальна, необходимо и достаточно, чтобы работа по перемещению заряда между двумя любыми точками поверхности равнялась нулю.
2)Эквипотенциальная поверхность ортогональна линиям напряженности. Действительно, работа по перемещению заряда между двумя точками эквипотенциальной поверхности:
![]() ,
так как
,
так как
![]()
Тогда:
![]() .
Это возможно, если cos=0,
т.е. =900
.
Это возможно, если cos=0,
т.е. =900
Например, эквипотенциальные поверхности поля отрицательного точечного заряда представляют собой сферические поверхности с центром, совпадающим с местом расположения заряда.
3)Поверхность заряженного проводника с установившимся распределением зарядов – эквипотенциальна.
На рис. 20 показаны линии напряженности и эквипотенциальные поверхности поля положительно заряженного проводника. Одна из эквипотенциальных поверхностей совпадает с его контуром
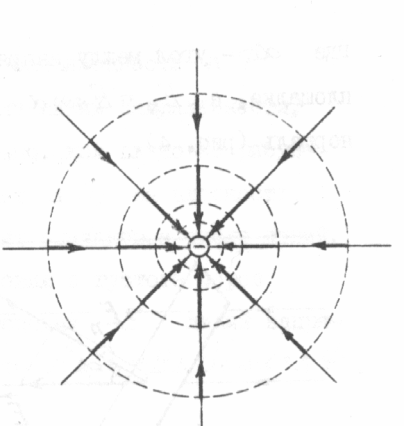
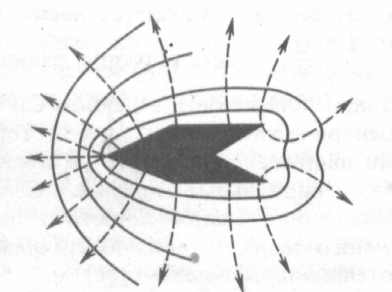
РИС.19 РИС.20
САМОСТ.IV: 1.Изобразить линии напряженности и эквипотенциальные поверхности поля:
а) положительного точечного заряда, б)двух равных точечных зарядов заряженных одноименно и разноименно,
в) зарядов равномерно распределенных по поверхности: сферы, бесконечной плоскости, бесконечного цилиндра.
2. Получить формулу для расчета потенциала точки поля заряда q равномерно распределенного по поверхности сферы радиусом R. Вычислить потенциал поверхности сферы.
§10 ОСНОВНАЯ ЗАДАЧА ЭЛЕКТРОСТАТИКИ.
Прямая задача – по известному распределению зарядов найти функциональную зависимость от координат для вектора напряженности и для потенциала.
Обратная задача - по известным функциям для вектора напряженности и потенциала рассчитать распределение зарядов в пространстве.
Для решения прямой задачи и однозначного определения вектора напряженности необходимо знать три скалярные функции. Поэтому получим связь между плотностью распределения зарядов и потенциалом.
![]() ,
,
![]() ,
,
![]() ,
,
![]() - оператор Лапласа (лапласиан),
псевдовектор
- оператор Лапласа (лапласиан),
псевдовектор
![]()
![]() - уравнение Пуассона, дифференциальное
уравнение второго порядка в частных
производных, которое позволяет при
заданном распределении зарядов и
известных начальных условиях найти
потенциал.
- уравнение Пуассона, дифференциальное
уравнение второго порядка в частных
производных, которое позволяет при
заданном распределении зарядов и
известных начальных условиях найти
потенциал.
При отсутствии в пространстве свободных
зарядов:
![]() - уравнение Лапласа.
- уравнение Лапласа.
Уравнения Пуассона и Лапласа позволяют (при известных начальных условиях) решить и прямую и обратную задачи электростатики.
